データ分布の正規性を判断するための 11 の基本的な方法

データ サイエンスと機械学習の分野では、多くのモデルはデータが正規分布していること、または正規分布の下でデータのパフォーマンスが優れていることを前提としています。たとえば、線形回帰は残差が正規分布していると仮定し、線形判別分析 (LDA) は正規分布などの仮定に基づいて導出されます。したがって、データ サイエンティストと機械学習の専門家にとって、データの正規性をテストする方法を理解することが重要です。

この記事の目的は、データの正規性をテストするための 11 の基本的な方法を紹介することです。読者はデータ分布の特性をよりよく理解し、分析に適切な方法を適用する方法を学びます。このようにして、モデルのパフォーマンスに対するデータ分散の影響をより適切に処理できるようになり、機械学習とデータ モデリングのプロセスがより便利になります。

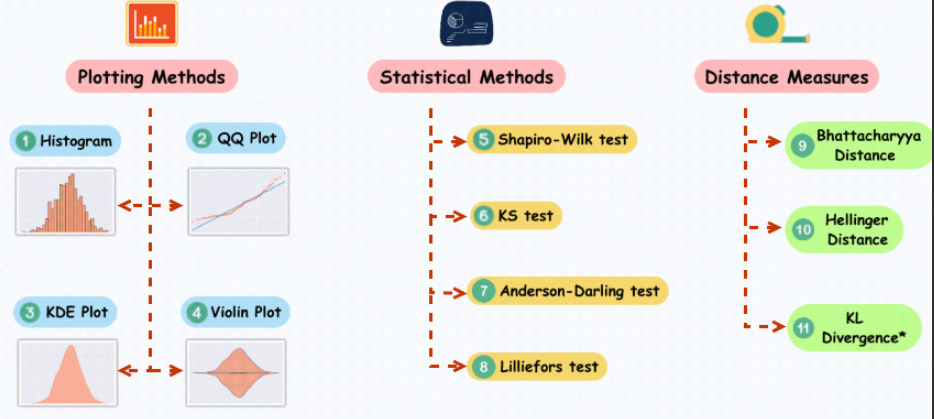
プロット方法

1.QQ プロット

QQ プロット (分位数-分位数プロット) は、データ分布が正規分布に準拠しているかどうかを確認するために広く使用されている方法です。 QQ プロットでは、データの分位点が標準正規分布の分位点と比較されます。データ分布が正規分布に近い場合、QQ プロット上の点は直線に近づきます。

QQ 図を示すために、以下のコード例は正規分布に従うランダム データのセットを生成します。コードを実行すると、QQ プロットと対応する正規分布曲線が表示されます。グラフ上の点の分布を観察することで、データが正規分布に近いかどうかを最初に判断できます

import numpy as npimport scipy.stats as statsimport matplotlib.pyplot as plt# 生成一组随机数据，假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制QQ图stats.probplot(data, dist="norm", plot=plt)plt.title('Q-Q Plot')plt.show()

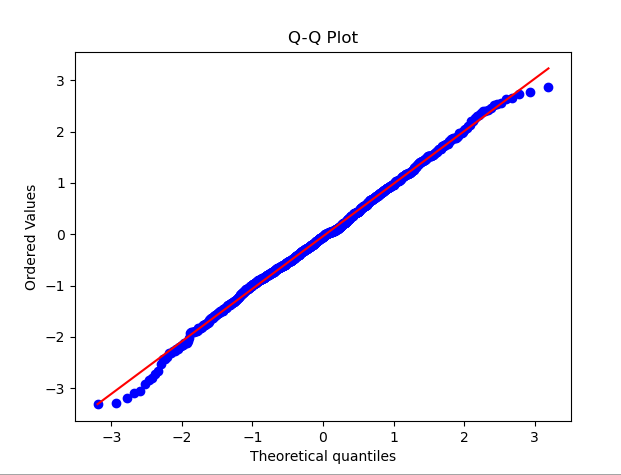
2.KDE Plot

KDE (カーネル密度推定) グラフはデータの分布を視覚化する方法であり、データの正規性を検出するのに役立ちます。 KDE プロットでは、データの密度を推定し、それを滑らかな曲線に描くことで、データの分布形状を観察するのに役立ちます。

KDE プロットをデモンストレーションするために、次のサンプル コードはセットを生成します。ランダムデータの正規分布。コードを実行すると、KDE ​​プロットと対応する正規分布曲線が表示され、視覚化を使用してデータ分布が正規性

import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=1000)# 创建KDE Plotsns.kdeplot(data, shade=True, label='KDE Plot')# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()

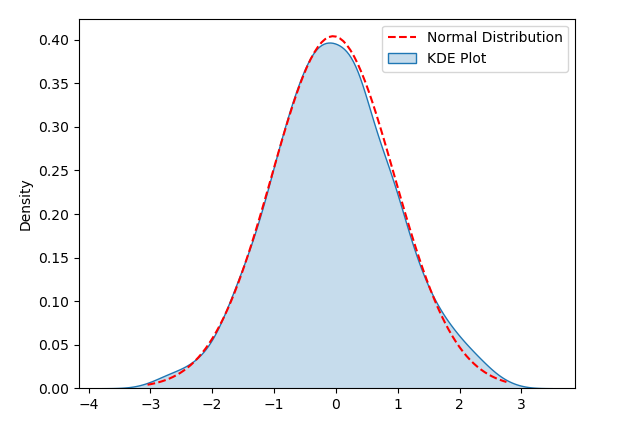
3.Violin プロットに準拠しているかどうかを検出できます。

Violin Plot を観察すると、データの分布形状がわかり、データが正規分布に近いかどうかを最初に判断できます。ヴァイオリン プロットが釣鐘曲線のような形状をしている場合、データはおそらくほぼ正規分布していると考えられます。 Violin Plot が大きく歪んでいたり、複数のピークがある場合、データは正規分布していない可能性があります。

次のサンプル コードは、バイオリン プロットを示すために正規分布に従うランダム データを生成するために使用されます。コードを実行すると、ヴァイオリン プロットと対応する正規分布曲線が表示されます。視覚化を通じてデータ分布の形状を検出し、最初にデータが正規分布に近いかどうかを判断します

import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=100)# 创建 Violin Plotsns.violinplot(data, inner="points")# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()

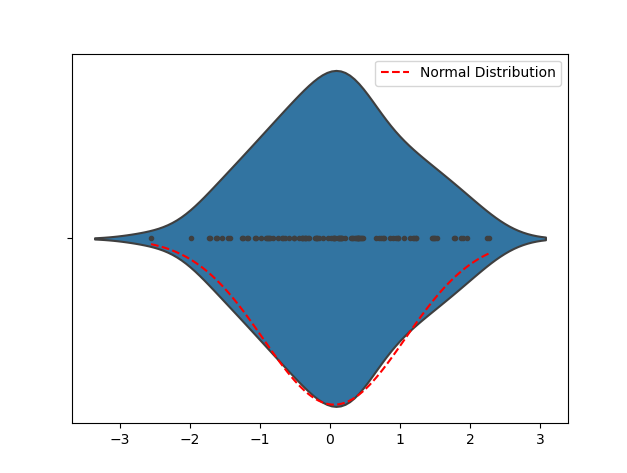
4.ヒストグラム

ヒストグラムを使用してテストしますデータ分布の正規性も一般的な方法です。ヒストグラムはデータの分布を直感的に理解するのに役立ち、データが正規分布に近いかどうかを事前に判断できます

import numpy as npimport matplotlib.pyplot as pltimport scipy.stats as stats# 生成一组随机数据，假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制直方图plt.hist(data, bins=30, density=True, alpha=0.6, color='g')plt.title('Histogram of Data')plt.xlabel('Value')plt.ylabel('Frequency')# 绘制正态分布的概率密度函数xmin, xmax = plt.xlim()x = np.linspace(xmin, xmax, 100)p = stats.norm.pdf(x, np.mean(data), np.std(data))plt.plot(x, p, 'k', linewidth=2)plt.show()

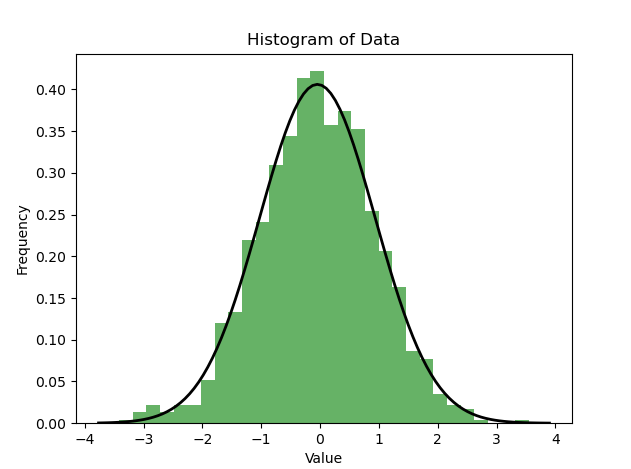
上の図に示すように、ヒストグラムが分布曲線が対応する正規分布曲線に類似している場合、データは正規分布に準拠している可能性があります。もちろん、可視化はあくまで予備的な判断であり、より正確な検出が必要な場合には、正規性検定などの統計的手法を用いて分析することも可能です。

統計的方法

5. シャピロ・ウィルク検定

シャピロ・ウィルク検定は、データが次の規則に準拠しているかどうかをテストするために使用される方法です。 Wテストと呼ばれます。 Shapiro-Wilk 検定を実行するときは、通常 2 つの主要な指標に焦点を当てます。

• 統計 W: 観測データと正規分布での期待値の間の相関に基づいて統計 W を計算します。 W の値の範囲は 0 ～ 1 です。W が 1 に近い場合、観測されたデータが正規分布によく適合していることを意味します。
• P 値: P 値は、この相関関係が観察される可能性を示します。P 値が有意水準 (通常は 0.05) より大きい場合、観察されたデータが正規分布に由来する可能性が高いことを示します。

したがって、統計量 W が 1 に近く、P 値が 0.05 より大きい場合、観測データは正規分布を満たしていると結論付けることができます。

次のコードでは、正規分布に従うランダム データのセットが最初に生成され、次に Shapiro-Wilk 検定が実行されて検定統計量と P 値が取得されます。 P 値と有意水準の比較に基づいて、標本データが正規分布に由来するかどうかを判断できます。

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Shapiro-Wilk检验stat, p = stats.shapiro(data)print('Shapiro-Wilk Statistic:', stat)print('P-value:', p)# 根据P值判断正态性alpha = 0.05if p > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

6.KS检验

KS检验（Kolmogorov-Smirnov检验）是一种用于检验数据是否符合特定分布（例如正态分布）的统计方法。它通过计算观测数据与理论分布的累积分布函数（CDF）之间的最大差异来评估它们是否来自同一分布。其基本步骤如下：

• 对两个样本数据进行排序。
• 计算两个样本的经验累积分布函数(ECDF)，即计算每个值在样本中的累积百分比。
• 计算两个累积分布函数之间的差异，通常使用KS统计量衡量。
• 根据样本的大小和显著性水平，使用参考表活计算p值判断两个样本是否来自同一分布。

Python中使用KS检验来检验数据是否符合正态分布时，可以使用Scipy库中的kstest函数。下面是一个简单的示例，演示了如何使用Python进行KS检验来检验数据是否符合正态分布。

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行KS检验statistic, p_value = stats.kstest(data, 'norm')print('KS Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

7.Anderson-Darling检验

Anderson-Darling检验是一种用于检验数据是否来自特定分布（例如正态分布）的统计方法。它特别强调观察值在分布尾部的差异，因此在检测极端值的偏差方面非常有效

下面的代码使用stats.anderson函数执行Anderson-Darling检验，并获取检验统计量、临界值以及显著性水平。然后通过比较统计量和临界值，可以判断样本数据是否符合正态分布

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Anderson-Darling检验result = stats.anderson(data, dist='norm')print('Anderson-Darling Statistic:', result.statistic)print('Critical Values:', result.critical_values)print('Significance Level:', result.significance_level)# 判断正态性if result.statistic <p style="text-align:center;"><img src="https://img.php.cn/upload/article/000/887/227/170255826239547.png" alt="データ分布の正規性を判断するための 11 の基本的な方法"></p><h4>8.Lilliefors检验</h4><p>Lilliefors检验（也被称为Kolmogorov-Smirnov-Lilliefors检验）是一种用于检验数据是否符合正态分布的统计检验方法。它是Kolmogorov-Smirnov检验的一种变体，专门用于小样本情况。与K-S检验不同，Lilliefors检验不需要假定数据的分布类型，而是基于观测数据来评估是否符合正态分布</p><p>在下面的例子中，我们使用lilliefors函数进行Lilliefors检验，并获得了检验统计量和P值。通过将P值与显著性水平进行比较，我们可以判断样本数据是否符合正态分布</p><pre class="brush:php;toolbar:false">import numpy as npfrom statsmodels.stats.diagnostic import lilliefors# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Lilliefors检验statistic, p_value = lilliefors(data)print('Lilliefors Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

9.距离测量Distance Measures

距离测量（Distance measures）是一种有效的测试数据正态性的方法，它提供了更直观的方式来比较观察数据分布与参考分布之间的差异。

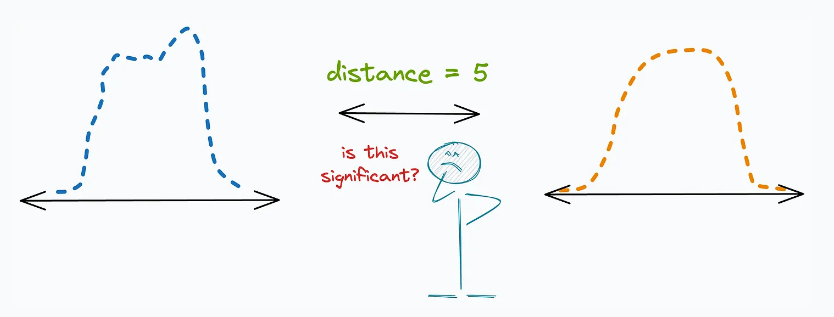
下面是一些常见的距离测量方法及其在测试正态性时的应用：

(1) "巴氏距离（Bhattacharyya distance）"的定义是：

• 测量两个分布之间的重叠，通常被解释为两个分布之间的接近程度。
• 选择与观察到的分布具有最小Bhattacharyya距离的参考分布，作为最接近的分布。

(2) 「海林格距离（Hellinger distance）」：

• 用于衡量两个分布之间的相似度，类似于Bhattacharyya距离。
• 与Bhattacharyya距离不同的是，Hellinger距离满足三角不等式，这使得它在一些情况下更为实用。

(3) "KL 散度（KL Divergence）"：

• 它本身并不是严格意义上的“距离度量”，但在测试正态性时可以用作衡量信息丢失的指标。
• 选择与观察到的分布具有最小KL散度的参考分布，作为最接近的分布。

运用这些距离测量方法，我们能够比对观测到的分布与多个参考分布之间的差异，进而更好地评估数据的正态性。通过找出与观察到的分布距离最短的参考分布，我们可以更精确地判断数据是否符合正态分布

以上がデータ分布の正規性を判断するための 11 の基本的な方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。