ホームページ >テクノロジー周辺機器 >AI >テレンス・タオが、60 年来の幾何学の新たな問題にアプローチします。定期的な閉鎖舗装の問題に新たなブレークスルーがもたらされました
テレンス・タオが、60 年来の幾何学の新たな問題にアプローチします。定期的な閉鎖舗装の問題に新たなブレークスルーがもたらされました
- PHPz転載
- 2023-10-14 14:17:071137ブラウズ
Tao Zhexuan は、周期的密舗装問題の研究において新たな進歩を遂げました。
9 月 18 日、Tao Zhexuan と Rachel Greenfeld は、プレプリントされた論文「Translational Single Mingling Pavement」を発表しました。 「並進モノタイリングの決定不可能性」をarXivにアップロードしました。

論文アドレス: https://arxiv.org/abs/2309.09504
この論文主な結論は、グリッドの次元が制限されていない場合、グリッドの有限サブセットがグリッドの周期サブセットをタイル化できるかどうかを決定する問題は決定できないということです。
次のことに注意してください。この問題は次元 1 と次元 2 で決定可能です。
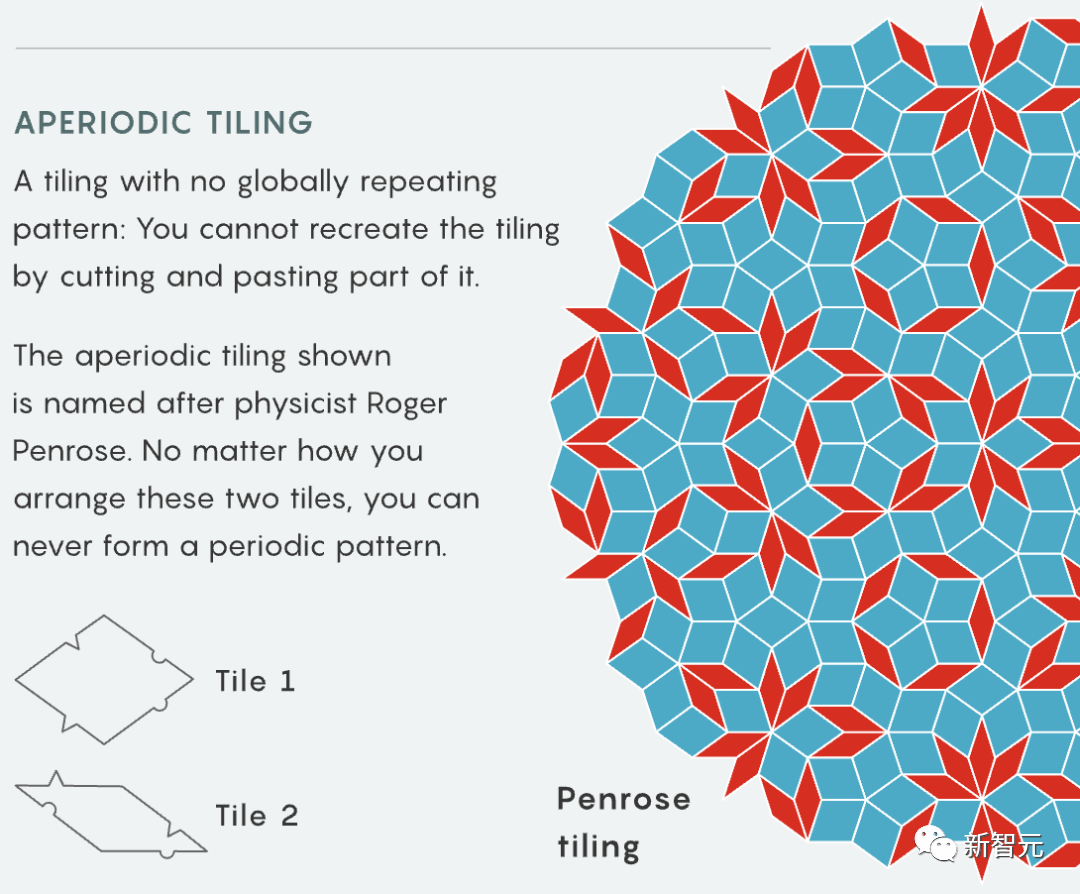
#Tao Zhexuan 氏は、この記事で紹介されているコンポーネントのほとんどが人気のあるゲームに似ているのは少し奇妙だと述べています—
ドミノ、数独、コンピュータ ゲーム「テトリス」、さらには子供向けゲーム「フィズ バズ」にさえ似たものがたくさんあります。
なぜ勉強するのか、なぜ勉強するのか数学の問題にはそんなにたくさんのゲームが含まれているのですか?テレンス・タオも説明できません

並進単一密タイリングの決定不可能性
この論文は、二人の以前の論文の続編。リンク周期タイル問題
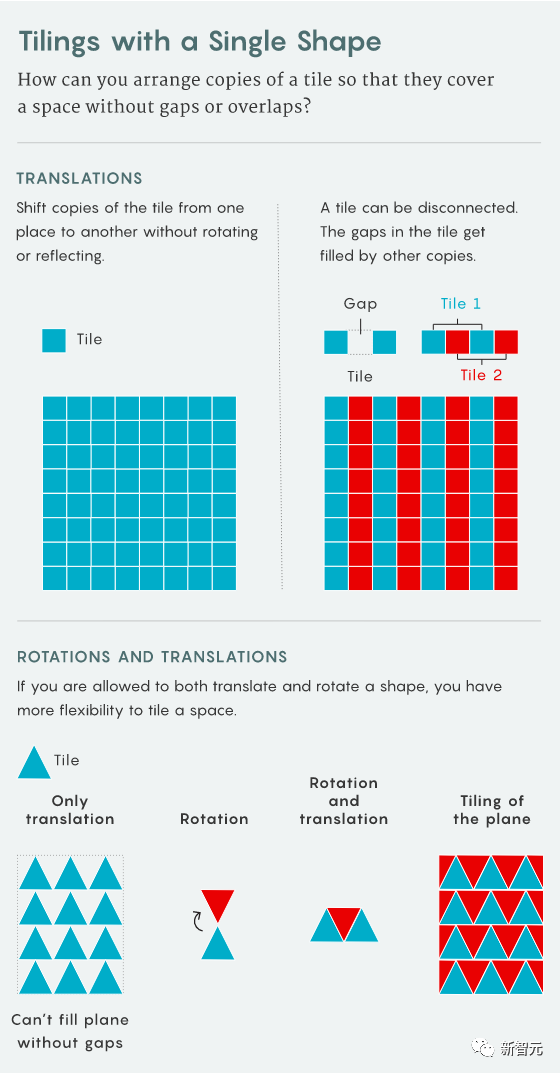
前回の論文では、高次元グリッドを構築しました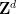 単一の密な舗装
単一の密な舗装 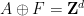
(したがって、単一の密な舗装 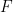 は有限集合です)。これは非周期的です。 (このタイルを周期タイル
は有限集合です)。これは非周期的です。 (このタイルを周期タイル 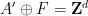 に「修正」する方法はありません。
に「修正」する方法はありません。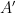 は有限インデックス サブグループ # を基準としています。 ## は定期的です)。
は有限インデックス サブグループ # を基準としています。 ## は定期的です)。 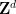

##(「ハット単密舗装」は、最近発見された非周期的等距離単密舗装です。
。この種の単密舗装では、回転の使用が許可されています。 、反射と変換、または新しい「ゴースト モノリス」。これらのモノリスは、反射が必要ないことを除いて、ハット モノリスに似ています)。 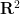 テレンス タオとレイチェル グリーンフェルドがこの予想を引き起こした理由の 1 つは、数学者ハオ ワンの観察です。
テレンス タオとレイチェル グリーンフェルドがこの予想を引き起こした理由の 1 つは、数学者ハオ ワンの観察です。
彼は、周期的テッセレーション予想が正しい場合、並進テッセレーション問題はアルゴリズムによって決定可能であることを発見しました—
次元 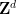 と有限部分集合
と有限部分集合 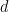 が与えられたとき、
が与えられたとき、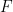 のチューリング マシンがあります。今回は、
のチューリング マシンがあります。今回は、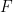 # を高密度に舗装できるかどうかを限られた時間内で判断できます。
# を高密度に舗装できるかどうかを限られた時間内で判断できます。 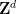 これは、周期的なタイリングがある場合は、コンピューター検索で見つけることができるためです。
これは、周期的なタイリングがある場合は、コンピューター検索で見つけることができるためです。
タイリングがまったくない場合は、次に、コンパクト性定理から、
素翻訳ではカバーできない限定された 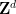 サブセットがいくつかあることがわかります。これは、コンピューター検索でも行うことができます。発見する。
サブセットがいくつかあることがわかります。これは、コンピューター検索でも行うことができます。発見する。 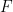 周期的テッセレーション予想は、考えられる状況はこれら 2 つだけであると主張し、決定可能性を与えます。
周期的テッセレーション予想は、考えられる状況はこれら 2 つだけであると主張し、決定可能性を与えます。
 一方、Wang の視点は不変です。周期的テッセレーション予想の失敗は、自動的に並進テッセレーション予想の失敗を意味するわけではありません。周期的タイリングの存在に依存しないタイリングを決定する他のアルゴリズムの存在を排除しないため、問題の決定不可能性
一方、Wang の視点は不変です。周期的テッセレーション予想の失敗は、自動的に並進テッセレーション予想の失敗を意味するわけではありません。周期的タイリングの存在に依存しないタイリングを決定する他のアルゴリズムの存在を排除しないため、問題の決定不可能性
(例: 新しく発見されたアルゴリズムを使用した場合でも)ハットとゴースト タイリングと同様に、
の有理係数を持つポリゴンの等角単一タイリング問題が、反射があるかどうかにかかわらず、決定可能であるかどうかはまだ未解決の問題です。 #この記事の主な結果は、この問題に対処しています (警告あり): 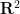
書き直す必要があるのは次のとおりです。定理 1

には、次元 、周期サブセットが与えられた場合、
にはアルゴリズムが存在しません。 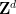 、および有限サブセット
、および有限サブセット 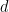 。限られた時間内に並進タイルがあるかどうかを判断できます
。限られた時間内に並進タイルがあるかどうかを判断できます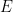 ##.
##. 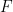
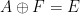
すべての 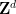 の代わりに
の代わりに 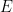 の周期的なサブセット
の周期的なサブセット 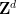 を使用する必要があることに注意してください。これは主にこのアプローチの技術的な制限によるものであり、追加の努力と創造性によって除去できる可能性があります。
を使用する必要があることに注意してください。これは主にこのアプローチの技術的な制限によるものであり、追加の努力と創造性によって除去できる可能性があります。
#さらに、テレンス タオとレイチェル グリーンフェルドは、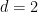 のとき、周期舗装予想がバタチャリヤによって確立されたことに気づきました。 #この場合、問題は特定できます。
のとき、周期舗装予想がバタチャリヤによって確立されたことに気づきました。 #この場合、問題は特定できます。 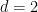
の固定値については、タイリングの問題が決定可能であるかどうかはまだ不明です (上記の結果では、寸法 が使用されていることに注意してください) 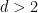 は固定ではなく、入力の一部です)。
は固定ではなく、入力の一部です)。 
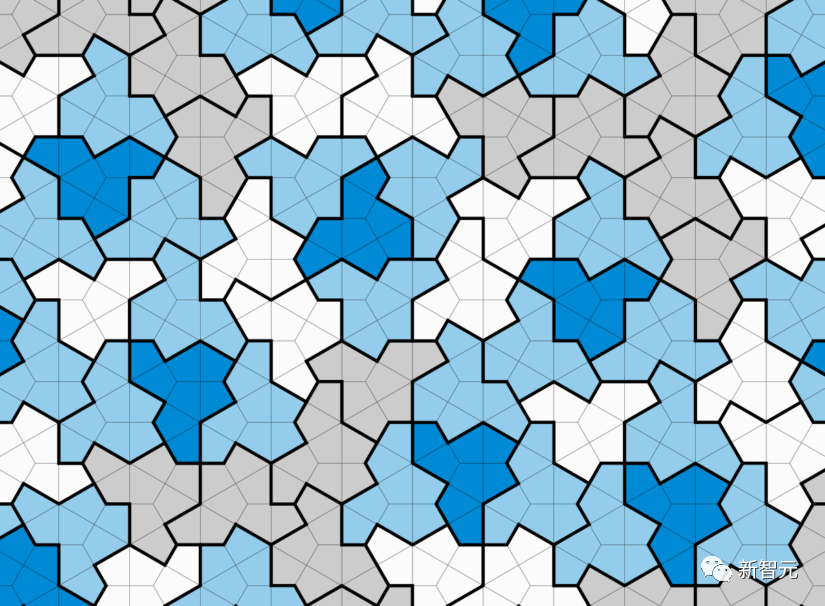 この定理はまた、アルゴリズム上の決定不能性と論理的決定不能性 (論理的独立性とも呼ばれます) の間のよく知られた関係により、次のことがわかります。次元
この定理はまた、アルゴリズム上の決定不能性と論理的決定不能性 (論理的独立性とも呼ばれます) の間のよく知られた関係により、次のことがわかります。次元
、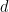
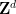 、# の (原理的に明確に記述可能な) 周期的なサブセットが存在します。 有限のサブセット
、# の (原理的に明確に記述可能な) 周期的なサブセットが存在します。 有限のサブセット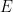 の
の 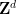 ##、したがって
##、したがって 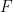 は並進タイリングを通過できます
は並進タイリングを通過できます 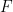 は ZFC 集合論では使用できません 確認あるいは改ざんする(もちろん理論が一貫していると仮定して)。
は ZFC 集合論では使用できません 確認あるいは改ざんする(もちろん理論が一貫していると仮定して)。 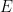 #このアプローチの結果、## の代わりに「ほぼ 2 次元」グループ
#このアプローチの結果、## の代わりに「ほぼ 2 次元」グループ
を使用することもできます。ここで #、 は有限アーベル群です (次元
は有限アーベル群です (次元 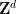 の代わりに入力の一部になります)。
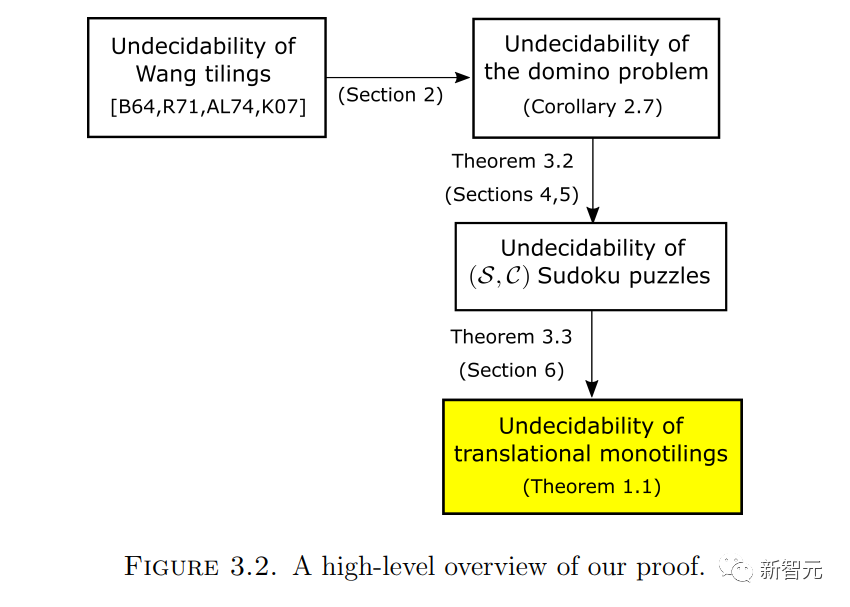
の代わりに入力の一部になります)。 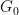 次に、証明の主なアイデアをいくつか説明します。
次に、証明の主なアイデアをいくつか説明します。 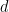
したがって、Wang の密舗装問題を 1 つの密舗装問題としてエンコードします。 ##2 番目の質問は、Wang の秘密ショップの問題に関するものです。 Wang の秘密ショップ セットが限定されているとします。 バーガーがかつてこの問題を決定することはできないと結論付けたことは有名です。 書き直す必要がある内容は次のとおりです: Berger、Robert、 この問題を高次元の並進単一密タイリング問題に変換するには、いくつかの中間問題を解決する必要があります まず、Wang の秘密ショップ問題を、ドミノ問題と呼ばれる同様の問題に簡単に埋め込むことができます。 次のように書き換えられます: ドミノ問題は問題 3です。 ドミノのレベル (または垂直) 有限セットが与えられた場合 、 は、水平または垂直に隣接し、同じエッジ色を持つ Wang の密なタイルのペアです。 #質問 4 (数独の問題) 指定された列幅 数独問題を単一の密な舗装問題に埋め込むことは、以前の論文で提案された修正方法に基づいています これらの論文でも提案されています異なるバージョン数独の問題を解析し、さまざまな問題 (数独の問題を含む) を 1 つのタイル問題に変換できる「タブ言語」と呼ばれるメソッドを作成しました。 ドミノ問題を数独の問題としてエンコードするには、ドミノ関数 (特定のドミノ セット 関連するドミノ制約と同じルールに従います) を取得し、それを使用して構築する必要があります。 Sudoku 関数 このアプローチはすぐにはわかりませんが、タオとレイチェル・グリーンフェルドはエマニュエル・ジャンデルの助けを借りてアデラーとルイスのアイデアの一部を採用し、特定の階層を使用して 1 つの質問をエンコードしました別のものに。 ここでは、階層構造 次に、式 は 2 つの異なる大きな素数です (たとえば、 の 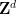 :
: 
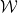 (単位 (平方、各エッジには限られたパレットから特定の色が割り当てられています)、隣接するタイルがエッジに同じ色を共有するように、標準グリッド
(単位 (平方、各エッジには限られたパレットから特定の色が割り当てられています)、隣接するタイルがエッジに同じ色を共有するように、標準グリッド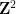 を使用して変換によって平面をテッセレーションすることは可能ですか?
を使用して変換によって平面をテッセレーションすることは可能ですか? 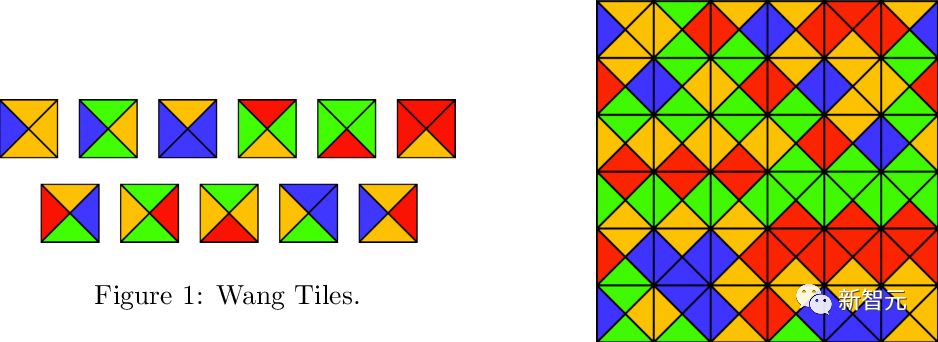


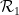 または
または 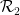 は隣接する単位正方形のペアであり、各単位正方形は有限集合 ## で表されます。 # の要素点で装飾するには
は隣接する単位正方形のペアであり、各単位正方形は有限集合 ## で表されます。 # の要素点で装飾するには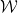 、標準格子タイリング
、標準格子タイリング 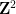 の各単位正方形に点を割り当てて、このタイリングの各ペアが水平 (または垂直) 正方形で のドミノを使用できるようにすることはできますか? ###### または #########?
の各単位正方形に点を割り当てて、このタイリングの各ペアが水平 (または垂直) 正方形で のドミノを使用できるようにすることはできますか? ###### または #########? 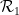
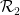 #実際には、各 Wang のタイルを個別の「ポイント」として挿入し、ドミノ セットを定義するだけです
#実際には、各 Wang のタイルを個別の「ポイント」として挿入し、ドミノ セットを定義するだけです
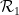 次のステップでは、ドミノの問題と数独の問題を組み合わせます:
次のステップでは、ドミノの問題と数独の問題を組み合わせます: 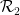

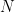 、数値のセット
、数値のセット 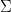 、関数のセット
、関数のセット 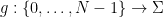
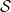 、および「初期条件」
、および「初期条件」 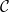 (ここでは詳しく説明しませんが)、「数独ボード」の
(ここでは詳しく説明しませんが)、「数独ボード」の 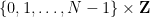 # の各セルに番号を割り当てることはできますか?
# の各セルに番号を割り当てることはできますか? 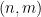 # # 任意の傾き
# # 任意の傾き 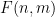 と切片
と切片 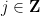 について、
について、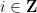 # 線 ## に沿った数値 # となります。は
# 線 ## に沿った数値 # となります。は 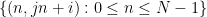 にあります (そして
にあります (そして 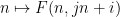 は初期条件
は初期条件 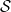 の対象となります)?
の対象となります)? 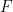
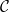
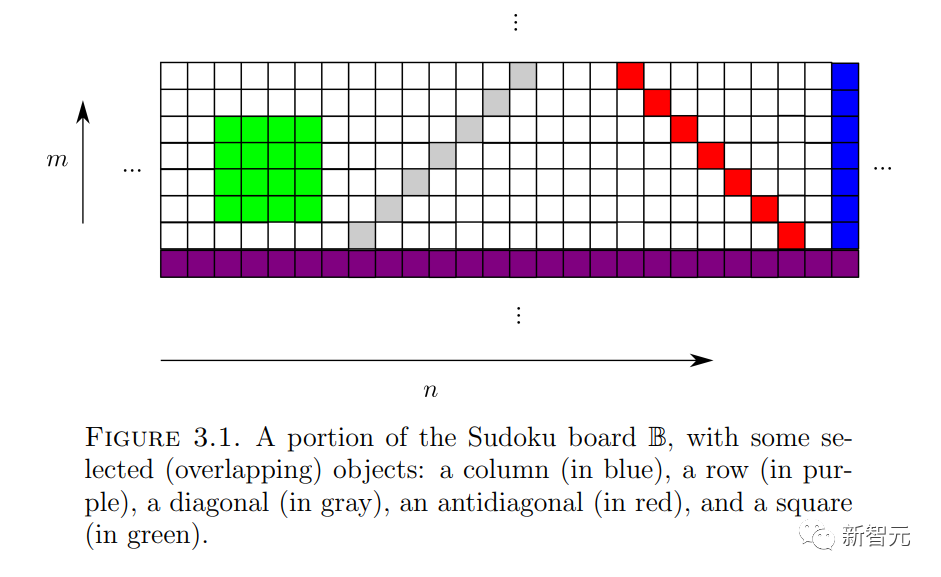
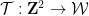 (ドミノ セットに関連付けられたいくつかの Sudoku 制約に従います); 逆に、それぞれは Sudoku パズルのルールに従います。 Sudoku 関数は、何らかの方法でドミノ関数から生成される必要があります。
(ドミノ セットに関連付けられたいくつかの Sudoku 制約に従います); 逆に、それぞれは Sudoku パズルのルールに従います。 Sudoku 関数は、何らかの方法でドミノ関数から生成される必要があります。 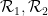
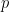 について説明します (ドミノ問題の 2 次元の性質により、2 つの異なる素数を使用する必要があります)。
について説明します (ドミノ問題の 2 次元の性質により、2 つの異なる素数を使用する必要があります)。 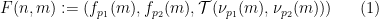 を使用して数独関数
を使用して数独関数 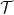 を作成します。これには何らかの埋め込みが行われます。
を作成します。これには何らかの埋め込みが行われます。 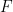 # ここで、
# ここで、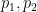 、## を使用できます) #)、
、## を使用できます) #)、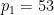 は
は 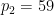 を
を 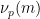 で割った回数を表し、
で割った回数を表し、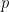
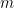 は、
は、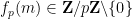 展開の最後のゼロ以外の数字です:
展開の最後のゼロ以外の数字です: 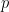
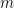 ##### ##########(#########、そして#########)。
##### ##########(#########、そして#########)。 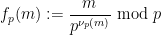 の場合、(1) の最初のコンポーネントは次のようになります:
の場合、(1) の最初のコンポーネントは次のようになります: 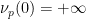 最終コンポーネント
最終コンポーネント 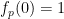 の典型的な例は次のようになります:
の典型的な例は次のようになります: 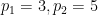 #興味深いはい、理由はわかりませんが、ここの装飾は基本的に子供向けゲーム「Fizz Buzz」のルールに従っています
#興味深いはい、理由はわかりませんが、ここの装飾は基本的に子供向けゲーム「Fizz Buzz」のルールに従っています
以上がテレンス・タオが、60 年来の幾何学の新たな問題にアプローチします。定期的な閉鎖舗装の問題に新たなブレークスルーがもたらされましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

