
遺伝的アルゴリズムの最適化パラメーター問題には、特定のコード例が必要です
要約:
遺伝的アルゴリズムは、進化のプロセスをシミュレートし、次のようなものに適用できる最適化アルゴリズムです。さまざまな最適化問題。この記事では、遺伝的アルゴリズムにおける最適化パラメーターの問題に焦点を当て、具体的なコード例を示します。
はじめに:
遺伝的アルゴリズムは、生物進化理論にヒントを得た最適化アルゴリズムであり、その基本的な考え方は、選択、交叉、突然変異などの操作をシミュレートすることにより、問題に対する最適な解決策を探索することです。進化の過程。遺伝的アルゴリズムには適応性と並列性という利点があり、複雑な目的関数と多数のパラメーターを伴う問題に広く使用されています。その中でも、パラメータの最適化の問題は、遺伝的アルゴリズムにおける重要な研究方向であり、実用化において広範な重要性を持っています。
- 遺伝的アルゴリズムの基本原理
遺伝的アルゴリズムの基本原理は、生物進化の選択、交叉、突然変異の操作をシミュレートして最適解を探索することです。まず、母集団と呼ばれる個人のグループがランダムに生成されます。各個人は、問題に対する考えられる解決策を表す一連のパラメータを持っています。次に、母集団内の個人は、特定の評価関数 (適応度関数) に従って評価されます。評価関数は、目的関数の値や制約条件の満足度など、問題の具体的な条件に応じて設計されるのが一般的です。評価関数の値が大きいほど優れた個体であることを示します。評価関数の結果に応じて一部の個体を親として選択し、一定の戦略に従って交叉・突然変異操作を行って新しい個体を生成します。新しい個体は元の個体群の一部の個体に取って代わり、次世代の個体群に入ります。停止基準が満たされるまで上記の操作を繰り返します。 - 最適化パラメータ問題
遺伝的アルゴリズムにおいて、最適化パラメータ問題とは、遺伝的アルゴリズムのパラメータを調整することによってアルゴリズムのパフォーマンスを向上させることを指します。一般的な最適化パラメータには、集団サイズ、交叉確率、突然変異確率などが含まれます。パラメーター問題を最適化する鍵は、アルゴリズムの検索効率と解の品質を向上させるために適切なパラメーター値を選択する方法です。 - 最適化パラメータ問題の解法
最適化パラメータ問題の解法には多くの方法がありますが、一般的な方法として遺伝的アルゴリズムによる適応調整法を以下に示します。この方法では、最適化パラメーターの値を動的に調整することで、アルゴリズムが問題の特性にさらに適応し、アルゴリズムのパフォーマンスを向上させることができます。
具体的な手順は以下のとおりです。
(1) 母集団と最適化パラメータの初期値を初期化します。
(2) 母集団内の個人の適応度値を計算します。
(3) 適応度値に基づいて親個体を選択します。
(4) 選択した親個体を元に交叉・突然変異操作を行い、新しい個体を生成します。
(5) 新しい個体の適応度を計算します。
(6) 適応度値に基づいて、次世代集団として新しい個体を選択します。
(7) 最適化パラメータの値を更新します。
(8) 停止基準を満たすまで手順(2)~(7)を繰り返します。
- コード例
次は、遺伝的アルゴリズムを使用して最適化パラメーターの問題を解決する方法を示す簡単な Python コードです。
import random
# 种群类
class Population:
def __init__(self, size):
self.size = size
self.individuals = []
for _ in range(size):
individual = Individual()
self.individuals.append(individual)
# 选择父代个体
def select_parents(self):
parents = []
for _ in range(size):
parent = random.choice(self.individuals)
parents.append(parent)
return parents
# 交叉和变异
def crossover_and_mutation(self, parents):
new_generation = []
for _ in range(size):
parent1 = random.choice(parents)
parent2 = random.choice(parents)
child = parent1.crossover(parent2)
child.mutation()
new_generation.append(child)
return new_generation
# 个体类
class Individual:
def __init__(self):
self.parameters = []
for _ in range(10):
parameter = random.uniform(0, 1)
self.parameters.append(parameter)
# 交叉操作
def crossover(self, other):
child = Individual()
for i in range(10):
if random.random() < 0.5:
child.parameters[i] = self.parameters[i]
else:
child.parameters[i] = other.parameters[i]
return child
# 变异操作
def mutation(self):
for i in range(10):
if random.random() < mutation_rate:
self.parameters[i] = random.uniform(0, 1)結論:
パラメータの最適化の問題は、遺伝的アルゴリズムにおける重要な研究方向であり、実際のアプリケーションにおいて幅広い応用価値があります。この記事では、遺伝的アルゴリズムの基本原理を紹介し、最適化パラメータ問題を解決するための具体的な方法、つまり遺伝的アルゴリズムの適応調整法を示します。同時に、遺伝的アルゴリズムを使用して最適化パラメーター問題を解決する方法を示す Python コードが提供されます。この記事が、遺伝的アルゴリズムにおけるパラメーター最適化問題の研究において読者に何らかの助けになれば幸いです。
以上が遺伝的アルゴリズムにおける最適化パラメータ問題の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
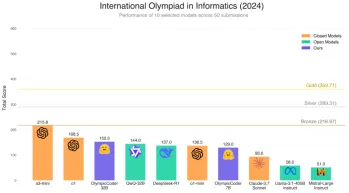 顔を抱きしめます&#039; S 7BモデルオリンピックコダーはClaude 3.7を破っていますか?Apr 23, 2025 am 11:49 AM
顔を抱きしめます&#039; S 7BモデルオリンピックコダーはClaude 3.7を破っていますか?Apr 23, 2025 am 11:49 AMFaceのOlympiccoder-7Bを抱き締める:強力なオープンソースコード推論モデル 優れたコードに焦点を当てた言語モデルを開発するための競争は激化しており、顔を抱き締めることは、恐るべき競争相手との競争に参加しました:Olympiccoder-7B、製品
 4つの新しいジェミニ機能は、見逃す余裕がありますApr 23, 2025 am 11:48 AM
4つの新しいジェミニ機能は、見逃す余裕がありますApr 23, 2025 am 11:48 AMAIが質問に答えるだけでなく、AIができることを望んでいる人は何人いますか?私は自分が持っていることを知っています、そして最近、私はそれがどのように変容しているかに驚いています。 aiチャットボットはもうチャットするだけでなく、作成することです。
 Camundaは、エージェントAIオーケストレーションの新しいスコアを作成しますApr 23, 2025 am 11:46 AM
Camundaは、エージェントAIオーケストレーションの新しいスコアを作成しますApr 23, 2025 am 11:46 AMSmart AIは、エンタープライズソフトウェアプラットフォームとアプリケーションのあらゆるレベルのレベルに統合され始めているため(強力なコアツールと信頼性の低いシミュレーションツールの両方があることを強調する必要があります)、これらのエージェントを管理するための新しいインフラストラクチャ機能のセットが必要です。 ドイツのベルリンに拠点を置くプロセスオーケストレーション会社であるCamundaは、Smart AIが適切な役割を果たし、新しいデジタル職場での正確なビジネス目標とルールと一致するのに役立つと考えています。同社は現在、組織がAIエージェントのモデル化、展開、管理を支援するように設計されたインテリジェントオーケストレーション機能を提供しています。 実用的なソフトウェアエンジニアリングの観点から、これはどういう意味ですか? 確実性と非決定的プロセスの統合 同社は、鍵はユーザー(通常はデータサイエンティスト、ソフトウェア)を許可することだと言いました
 キュレーションされたエンタープライズAIエクスペリエンスに価値はありますか?Apr 23, 2025 am 11:45 AM
キュレーションされたエンタープライズAIエクスペリエンスに価値はありますか?Apr 23, 2025 am 11:45 AM次の'25年にGoogle Cloudに参加して、GoogleがどのようにAIの製品を区別するかを見たいと思っていました。 エージェントスペース(ここで説明)とカスタマーエクスペリエンススイート(ここで説明)に関する最近の発表は、ビジネス価値を強調し、
 ぼろきれに最適な多言語埋め込みモデルを見つける方法は?Apr 23, 2025 am 11:44 AM
ぼろきれに最適な多言語埋め込みモデルを見つける方法は?Apr 23, 2025 am 11:44 AM検索拡張生成(RAG)システムのための最適な多言語埋め込みモデルの選択 今日の相互接続された世界では、効果的な多言語AIシステムを構築することが最重要です。 REには、堅牢な多言語埋め込みモデルが重要です
 ムスク:オースティンのロボタキシスは、10,000マイルごとに介入が必要ですApr 23, 2025 am 11:42 AM
ムスク:オースティンのロボタキシスは、10,000マイルごとに介入が必要ですApr 23, 2025 am 11:42 AMテスラのオースティンロボタキシローンチ:マスクの主張を詳しく見る Elon Muskは最近、テキサス州オースティンでのテスラの今後のRobotaxi発売を発表しました。当初、安全上の理由で10〜20台の車両の小さな艦隊を展開し、迅速な拡大を計画しました。 h
 AI&#x27;の衝撃的なピボット:作業ツールからデジタルセラピストやライフコーチまでApr 23, 2025 am 11:41 AM
AI&#x27;の衝撃的なピボット:作業ツールからデジタルセラピストやライフコーチまでApr 23, 2025 am 11:41 AM人工知能の適用方法は予期しない場合があります。当初、私たちの多くは、それが主にコードの作成やコンテンツの作成など、創造的で技術的なタスクに使用されていると思うかもしれません。 ただし、Harvard Business Reviewによって報告された最近の調査では、そうではないことが示されています。ほとんどのユーザーは、仕事だけでなく、サポート、組織、さらには友情のために人工知能を求めています! 報告書は、AIアプリケーションの最初のケースは治療と交際であると述べています。これは、その24時間年中無休の可用性と匿名の正直なアドバイスとフィードバックを提供する能力が非常に価値があることを示しています。 一方、マーケティングタスク(ブログの作成、ソーシャルメディアの投稿の作成、広告コピーなど)は、一般的な使用リストではるかに低くランク付けされています。 なぜこれがなぜですか?研究の結果とそれがどのように続くかを見てみましょう
 企業はAIエージェントの採用に向けて競い合っていますApr 23, 2025 am 11:40 AM
企業はAIエージェントの採用に向けて競い合っていますApr 23, 2025 am 11:40 AMAIエージェントの台頭は、ビジネス環境を変えています。 Cloud Revolutionと比較して、AIエージェントの影響は指数関数的に大きく、知識作業に革命をもたらすことを約束していると予測されています。 人間の意思決定-makiをシミュレートする能力


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

SublimeText3 Linux 新バージョン
SublimeText3 Linux 最新バージョン

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

SecLists
SecLists は、セキュリティ テスターの究極の相棒です。これは、セキュリティ評価中に頻繁に使用されるさまざまな種類のリストを 1 か所にまとめたものです。 SecLists は、セキュリティ テスターが必要とする可能性のあるすべてのリストを便利に提供することで、セキュリティ テストをより効率的かつ生産的にするのに役立ちます。リストの種類には、ユーザー名、パスワード、URL、ファジング ペイロード、機密データ パターン、Web シェルなどが含まれます。テスターはこのリポジトリを新しいテスト マシンにプルするだけで、必要なあらゆる種類のリストにアクセスできるようになります。

SublimeText3 中国語版
中国語版、とても使いやすい

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)






