迷路内のマウスのための C プログラム - バックトラッキング-2
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-09-11 14:25:21737ブラウズ
迷路の中のネズミも、バックトラッキングを使用する一般的な問題です。 I
迷路は、いくつかのセルがブロックされている 2 次元マトリックスです。セルの 1 つはソース セルであり、そこから開始する必要があります。もう一つは目的地、つまり私たちが到達しなければならない場所です。ブロックされたセルに入らずに、送信元から宛先までのパスを見つける必要があります。未解決の迷路の写真を以下に示します。

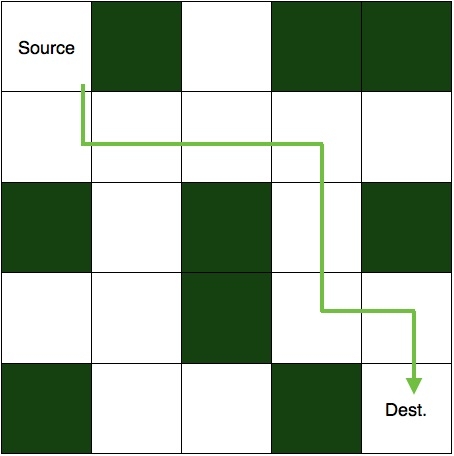
Input:
maze[][] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}}
Output:
1 0 0 0 0
1 1 1 1 0
0 0 0 1 0
0 0 0 1 1
0 0 0 0 1説明まず、迷路を表す行列を作成します。行列の要素は 0 または 1 になります。1 はブロックされたセルを意味し、0 は移動できるセルを意味します。上に示した迷路の行列は次のとおりです。 0 1 0 1 1 0 0 0 0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 1 0次に、同じ次元の別の行列を作成して、解を保存します。その要素も 0 または 1 になります。1 はパス内のセルを表し、残りのセルは 0 になります。解を表す行列は次のとおりです。
1 0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1これで、行列が完成しました。次に、開始セルからターゲット セルまでのパスを見つけます。実行する手順は次のとおりです。
- 現在のセルを確認し、それがターゲット セルである場合は、パズルは解けました。
- そうでない場合は、下に移動して、次のセルに移動できるかどうかを確認してください (セルに移動するには、セルが空であり、パス内にない必要があります)。
- 次のセルに移動できる場合は、パスに沿って次の下のセルまで移動を続けます。 #そうでない場合は、右に移動してみてください。右側がブロックされているか占有されている場合は、上に移動します。
- 同様に、上に移動できない場合は、単純に左のセルに移動します。
- 4 つの方向 (下、右、上、左) のいずれにも移動できない場合は、単純に戻って現在のパスを変更します (バックトラック)。
- つまり、要約すると、現在のセルから他のセル (下、右、上、左) に移動しようとし、移動できない場合は戻り、セルの方向を決定します。パスが別のセルに変更されます。
printsolution → この関数は単純に解行列を出力します。
solvemaze → これはバックトラッキングアルゴリズムを実際に実装する関数です。まず、セルがターゲット セルであるかどうかを確認します。ターゲット セルである場合は (r==SIZE-1) および (c==SIZE-1) となります。それがターゲットのセルであれば、パズルは解けたことになります。そうでない場合は、それが有効なモバイルセルであるかどうかを確認します。有効なセルが行列内に存在する必要があります。つまり、インデックスは 0 から SIZE-1 の間でなければならず、r>=0 && c>=0 && r 例 以上が迷路内のマウスのための C プログラム - バックトラッキング-2の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。#include <iostream>
using namespace std;
#define SIZE 5
//the maze problem
int maze[SIZE][SIZE] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}
};
//matrix to store the solution
int solution[SIZE][SIZE];
//function to print the solution matrix
void printsolution() {
int i,j;
for(i=0;i<SIZE;i++) {
for(j=0;j<SIZE;j++) {
printf("%d\t",solution[i][j]);
}
printf("</p><p></p><p>");
}
}
//function to solve the maze
//using backtracking
int solvemaze(int r, int c) {
//if destination is reached, maze is solved
//destination is the last cell(maze[SIZE-1][SIZE-1])
if((r==SIZE-1) && (c==SIZE-1) {
solution[r][c] = 1;
return 1;
}
//checking if we can visit in this cell or not
//the indices of the cell must be in (0,SIZE-1)
//and solution[r][c] == 0 is making sure that the cell is not already visited
//maze[r][c] == 0 is making sure that the cell is not blocked
if(r>=0 && c>=0 && r<SIZE && c<SIZE && solution[r][c] == 0 && maze[r][c] == 0){
//if safe to visit then visit the cell
solution[r][c] = 1;
//going down
if(solvemaze(r+1, c))
return 1;
//going right
if(solvemaze(r, c+1))
return 1;
//going up
if(solvemaze(r-1, c))
return 1;
//going left
if(solvemaze(r, c-1))
return 1;
//backtracking
solution[r][c] = 0;
return 0;
}
return 0;
}
int main() {
//making all elements of the solution matrix 0
int i,j;
for(i=0; i<SIZE; i++) {
for(j=0; j<SIZE; j++) {
solution[i][j] = 0;
}
}
if (solvemaze(0,0))
printsolution();
else
printf("No solution</p><p>");
return 0;
}

