ホームページ >テクノロジー周辺機器 >AI >深い思考 | 大規模モデルの機能境界はどこにあるのでしょうか?
深い思考 | 大規模モデルの機能境界はどこにあるのでしょうか?
- PHPz転載
- 2023-09-08 17:41:051339ブラウズ
無限のデータ、無限の計算能力、無限のモデル、完璧な最適化アルゴリズム、汎化パフォーマンスなどの無限のリソースがある場合、結果として得られる事前トレーニング済みモデルを使用してすべての問題を解決できるでしょうか? ?
これは誰もが非常に懸念している質問ですが、既存の機械学習理論では答えることができません。モデルは無限であり、表現能力も当然無限であるため、表現能力理論とは何の関係もありません。また、アルゴリズムの最適化と一般化のパフォーマンスは完璧であると仮定しているため、最適化と一般化の理論とは無関係です。言い換えれば、これまでの理論研究の問題はここではもはや存在しません。
今日は、ICML'2023で発表した論文「On the Power of Foundation Models」を紹介し、圏論の観点から答えを出します。
圏論とは何ですか?
数学を専攻していない方は、圏論に馴染みがないかもしれません。圏論は数学の中の数学と呼ばれ、現代数学の基本言語を提供します。現代のほぼすべての数学分野は、代数トポロジー、代数幾何学、代数グラフ理論など、圏論の言語で記述されています。圏論は構造と関係の研究です。集合論の自然な拡張と見ることができます。集合論では、集合にはいくつかの異なる要素が含まれています。圏論では、要素を記録するだけでなく、要素間の関係も記録します。
Martin Kuppe はかつて数学の地図を描き、圏論を地図の一番上に置き、数学のすべての分野に光を当てました:
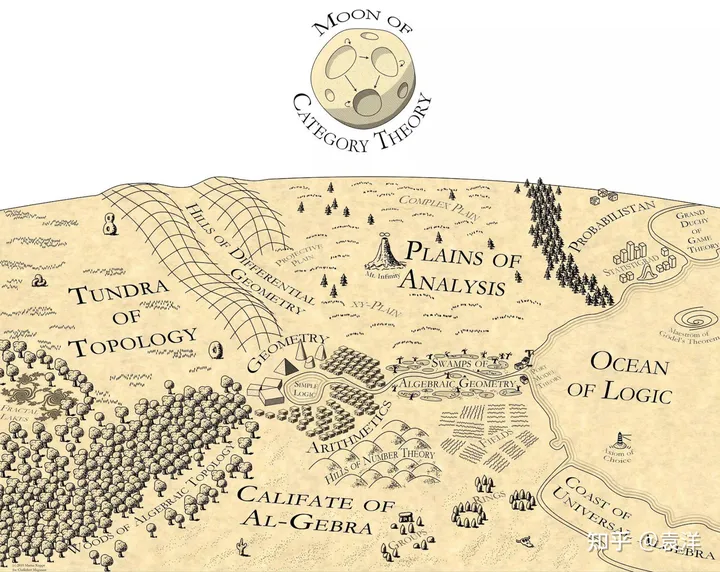
圏論についてインターネット上には多くの紹介がありますが、ここではいくつかの基本的な概念について簡単に説明します:

#教師あり学習の圏論の視点
##過去 10 年ほどの間、教師あり学習フレームワークを中心に多くの研究が行われ、多くの素晴らしい結論が得られました。ただし、このフレームワークは AI アルゴリズムに対する人々の理解を制限するものでもあり、事前にトレーニングされた大規模なモデルを理解することが非常に困難になります。たとえば、既存の一般化理論では、モデルのクロスモーダル学習機能を説明するのが困難です。 
 このファンクターの入力データと出力データをサンプリングすることで、このファンクターを学習できるでしょうか?
このファンクターの入力データと出力データをサンプリングすることで、このファンクターを学習できるでしょうか?
このプロセスでは、2 つのカテゴリ X と Y の内部構造を考慮していないことに注意してください。実際、教師あり学習ではカテゴリ内の構造について何の仮定も行わないため、2 つのカテゴリ内の 2 つのオブジェクト間には関係がないと考えることができます。したがって、X と Y は 2 つのセットとみなすことができます。現時点では、一般化理論の有名なノー フリー ランチ定理は、追加の仮定がなければ (大量のサンプルがない限り) X から Y へのファンクターを学習することは不可能であることを示しています。
一見すると、この新しい視点は役に立ちません。カテゴリに制約を追加する場合でも、ファンクターに制約を追加する場合でも、本質的な違いはないようです。実際、新しい観点は従来のフレームワークの去勢版に似ています。損失関数の概念さえ言及されていません。損失関数は教師あり学習において非常に重要であり、トレーニングの収束特性や汎化特性の分析には使用できません。アルゴリズム。では、この新しい視点をどのように理解すればよいのでしょうか? 
自己教師あり学習のカテゴリー理論の視点
トレーニング前のタスクとカテゴリー
# #まず、事前トレーニング タスクでのカテゴリの定義を明確にしましょう。実際、事前トレーニング タスクを設計しない場合、カテゴリ内のオブジェクト間に関係はありませんが、事前トレーニング タスクを設計した後、人間の事前知識をタスクの形式でカテゴリに注入します。
そして、これらの構造は、大きなモデルが所有する知識になります。 #########具体的には:###

言い換えると、データ セットに対して事前トレーニング タスクを定義するときは、対応する関係構造を含むカテゴリを定義します。事前トレーニング タスクの学習目標は、モデルにこのカテゴリをよく学習させることです。具体的には、理想モデルの概念を検討します。
理想的なモデル

ここで、「データにとらわれない」とは、 データを見る前にただし、添字 f は、2 つの関数 f と がブラック ボックス呼び出しを通じて使用できることを意味します。言い換えれば、 は「単純な」関数ですが、モデル f の機能を利用してより複雑な関係を表すことができます。これを理解するのは簡単ではないかもしれませんが、圧縮アルゴリズムを例にとって考えてみましょう。圧縮アルゴリズム自体はデータに依存する場合があり、たとえばデータ分散用に特別に最適化される場合があります。ただし、データ非依存関数 として、データ配布にアクセスすることはできませんが、「圧縮アルゴリズムの呼び出し」の操作がデータに依存しないため、圧縮アルゴリズムを呼び出してデータを解凍することはできます。
さまざまな事前トレーニング タスクに対して、さまざまな :

したがって、次のように言えます: プロセス事前トレーニングの学習は、理想的なモデル f を見つけるプロセスです。
ただし、 が確実であるとしても、定義上、理想的なモデルは一意ではありません。理論的には、モデル f は非常にインテリジェントであり、C でデータを学習せずに何でもできる可能性があります。この場合、 f の機能について意味のある記述をすることはできません。したがって、問題の反対側を見る必要があります。
事前学習済みタスクによって定義されたカテゴリ C が与えられた場合、任意の理想 f に対して、どのタスクを解決できますか?
これは、この記事の冒頭で答えたい核心的な質問です。まず重要な概念を紹介しましょう。
米田埋め込み
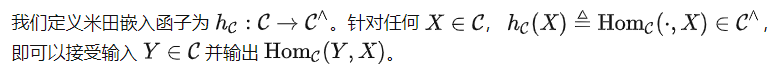

## がであることを証明するのは簡単です能力 他の理想モデル f が与えられると、 内のすべての関係も f に含まれるため、最も弱い理想モデル。同時に、これは、他の追加の仮定なしで事前トレーニング モデルを学習するという究極の目標でもあります。したがって、私たちの核心的な質問に答えるために、以下で特に を検討します。
プロンプトチューニング: たくさん見ることによってのみ多くを学ぶことができます

米田補題

これら 2 つの表現を使用して T(X) を計算できます。 。ただし、クエスト プロンプト P は ではなく 経由で送信する必要があることに注意してください。つまり、T ではなく (P) を ## として取得することになります。 # の入力。これは圏論における別の重要な定義につながります。
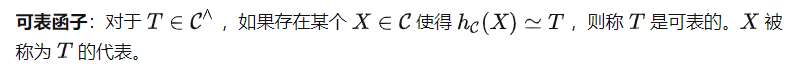 この定義に基づいて、次の定理が得られます(証明は省略)。
この定義に基づいて、次の定理が得られます(証明は省略)。
 アルゴリズムを調整するためのヒントの一部は、必ずしもカテゴリ C に含まれるわけではないことに注意してください。特徴空間での表現になります。このアプローチには、表現可能なタスクよりも複雑なタスクをサポートできる可能性がありますが、機能強化は特徴空間の表現力に依存します。以下に、定理 1 の簡単な帰結を示します。
アルゴリズムを調整するためのヒントの一部は、必ずしもカテゴリ C に含まれるわけではないことに注意してください。特徴空間での表現になります。このアプローチには、表現可能なタスクよりも複雑なタスクをサポートできる可能性がありますが、機能強化は特徴空間の表現力に依存します。以下に、定理 1 の簡単な帰結を示します。
. 画像の回転角度を予測する事前トレーニング タスク [4] の場合、プロンプト調整ではセグメンテーションや分類などの複雑な下流タスクを解決できません。 証明: 画像の回転角度を予測する事前トレーニング タスクでは、指定された画像を 4 つの異なる角度 (0°、90°、180°、270°) で回転させ、モデルに予測を行わせます。したがって、この事前トレーニング タスクによって定義されたカテゴリは、各オブジェクトを 4 つの要素のグループに配置します。明らかに、セグメンテーションや分類などのタスクは、そのような単純なオブジェクトでは表現できません。 系 1 は少し直観に反します。元の論文 [4] では、この方法を使用して取得されたモデルは分類やセグメンテーションなどの下流タスクを部分的に解決できると述べられているからです。ただし、私たちの定義では、タスクを解決するとは、モデルが すべての入力 に対して正しい出力を生成する必要があることを意味するため、部分的に正しいことは成功とみなされません。これは、記事の冒頭で述べた質問とも一致します。無制限のリソースのサポートにより、画像の回転角度を予測する事前トレーニングされたタスクを使用して、複雑な下流タスクを解決できますか?系 1 では否定的な答えが得られます。 調整能力には限界があるというヒントでは、微調整アルゴリズムはどうなるのでしょうか?米田関手展開定理 ([5] の命題 2.7.1 を参照) に基づいて、次の定理を得ることができます。 定理 2 で考慮される下流タスクは、データセット内のデータ内容ではなく、C の構造に基づいています。したがって、回転した画像の角度を予測するという前述の事前トレーニング タスクによって定義されたカテゴリは、依然として非常に単純なグループ構造を持っています。しかし、定理 2 によれば、より多様なタスクを解決するためにそれを使用できます。たとえば、すべてのオブジェクトを同じ出力にマップできますが、これはヒント チューニングでは不可能です。定理 2 は、事前トレーニング タスクの重要性を明らかにしています。より優れた事前トレーニング タスクにより、より強力なカテゴリ C が作成され、モデルの微調整の可能性がさらに向上します。 定理 2 については、よくある誤解が 2 つあります。まず第一に、たとえカテゴリ C に大量の情報が含まれているとしても、定理 2 は大まかな上限を提供するだけであり、 は C にすべての情報を記録し、あらゆるタスクを解決できる可能性があると述べています。どのアルゴリズムを微調整してもこの目的は達成できるとは言えません。第 2 に、定理 2 は一見すると過剰にパラメータ化された理論のように見えます。ただし、彼らは自己教師あり学習のさまざまなステップを分析しています。パラメトリック分析は事前トレーニングのステップです。つまり、特定の仮定の下では、モデルが十分に大きく学習率が十分に小さい限り、事前トレーニング タスクの最適化エラーと一般化エラーは非常に小さくなります。定理 2 は、事前トレーニング後の微調整ステップを分析し、このステップには大きな可能性があると述べています。 教師あり学習と自己教師あり学習。機械学習の観点から見ると、自己教師あり学習は依然として教師あり学習の一種ですが、ラベルを取得する方法はより賢明です。しかし、カテゴリー理論の観点から見ると、自己教師あり学習はカテゴリー内の構造を定義し、教師あり学習はカテゴリー間の関係を定義します。したがって、それらは人工知能マップの異なる部分に存在し、まったく異なることを行っています。 該当シーン。この記事の冒頭で無限のリソースの仮定が検討されたため、多くの友人は、これらの理論は虚空の中でのみ真に確立できると考えるかもしれません。これはそうではありません。実際の導出プロセスでは、理想的なモデルと事前定義された関数 のみを考慮しました。実際、 が決定されている限り、事前トレーニングされたモデル f (ランダムな初期化段階であっても) は入力 XC の f(X) を計算し、 を使用して次のことを行うことができます。 2 つのオブジェクト間の関係を計算します。言い換えれば、 が決定されている限り、各事前トレーニング モデルはカテゴリに対応しており、事前トレーニングの目標は、このカテゴリを事前トレーニング タスクで定義されたカテゴリと継続的に一致させることだけです。 。したがって、私たちの理論はすべての事前トレーニング済みモデルに当てはまります。 コアフォーミュラ。 AI に本当に一連の理論的裏付けがあるのなら、その背後には 1 つまたはいくつかのシンプルで美しい公式があるはずだ、と多くの人が言います。大規模モデルの機能を説明するために圏論の公式を使用する必要がある場合、それは前に述べたものになるはずだと思います: 大規模モデルに精通している人向け, この式の意味を深く理解すると、この式はナンセンスだと感じるかもしれませんが、これは現在の大きなモデルの動作モードを書き出すためのより複雑な数式にすぎません。 しかし、それは真実ではありません。現代科学は数学に基づいており、現代数学は圏論に基づいており、圏論の最も重要な定理は米田の補題です。私が書いた式は米田補題の同型写像を非対称版に分解したものですが、大きなモデルの開き方とまったく同じです。 これは偶然ではないと思います。圏論が現代数学のさまざまな分野を解明できるのであれば、一般的な人工知能の進むべき道も明らかにできるでしょう。 この記事は、北京知源人工知能研究所のQianfangチームとの長期にわたる緊密な協力に基づいています。 元のリンク: https://mp.weixin.qq.com/s/bKf3JADjAveeJDjFzcDbkw微調整: 情報を失わずに表現
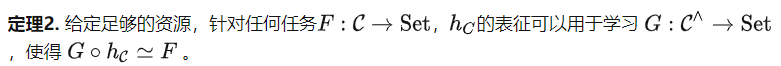
ディスカッションと要約

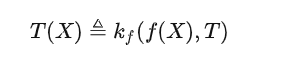

以上が深い思考 | 大規模モデルの機能境界はどこにあるのでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

