指定されたバイナリ ツリー内で最大のバイナリ検索サブツリーを見つける - C++ のエピソード 1
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-08-31 15:33:07725ブラウズ
この問題では、二分木 BT が与えられます。私たちのタスクは、指定された二分木で 最大の二分検索サブツリーを見つけることです。
バイナリ ツリーは、データの保存に使用される特別なデータ構造です。バイナリ ツリーには、各ノードが最大 2 つの子ノードを持つことができるという特別な条件があります。
二分探索木 (BST) は、次の特性を満たす木です。
左のサブツリーのキー値が親ノードのキー値より小さい(ルートノード) の値。
右サブツリーのキー値は、その親ノード (ルート ノード) のキー値以上です。
この問題を理解するために例を挙げてみましょう。
次のように入力してください:
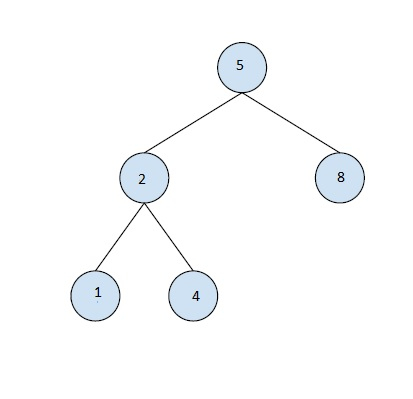
出力: 3
説明
Full binary tree is a BST.
解決策
問題を解決する簡単な方法は、ツリーを順番に走査することです。ツリーの各ノードについて、そのサブツリーが二分探索ツリーであるかどうかを確認します。最後に、最大の二分探索サブツリーのサイズが返されます。
例
ソリューションがどのように機能するかを示す手順の例
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findTreeSize(node* node) {
if (node == NULL)
return 0;
else
return(findTreeSize(node->left) + findTreeSize(node->right) + 1);
}
int isBSTree(struct node* node) {
if (node == NULL)
return 1;
if (node->left != NULL && node->left->data > node->data)
return 0;
if (node->right != NULL && node->right->data < node->data)
return 0;
if (!isBSTree(node->left) || !isBSTree(node->right))
return 0;
return 1;
}
int findlargestBSTSize(struct node *root) {
if (isBSTree(root)){
return findTreeSize(root);
}
else
return max(findlargestBSTSize(root->left), findlargestBSTSize(root->right));
}
int main() {
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The size of the largest possible BST is "<<findlargestBSTSize(root);
return 0;
}出力
The size of the largest possible BST is 5
別のアプローチ
別のアプローチこの問題を解決する方法は、ツリーを下からたどって、その子ノードによって BST であるかどうかを確認することです。これを行うために、
が BST であるかどうかを追跡します。
左側のサブツリーの場合、最大の要素の値。
右側のサブツリーの場合、最小要素の値。 BST を確認するには、これらの値を現在のノードと比較する必要があります。
さらに、最大 BST のサイズは、現在の BST のサイズと比較することによって更新されます。
例
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findlargestBSTSizeRec(node* node, int *minValRsubTree, int *maxValLsubTree, int *maxBSTSize, bool *isBSTree) {
if (node == NULL){
*isBSTree = true;
return 0;
}
int min = INT_MAX;
bool left_flag = false;
bool right_flag = false;
int leftSubtreeSize,rightSubTreeSize;
*maxValLsubTree = INT_MIN;
leftSubtreeSize = findlargestBSTSizeRec(node->left, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data > *maxValLsubTree)
left_flag = true;
min = *minValRsubTree;
*minValRsubTree = INT_MAX;
rightSubTreeSize = findlargestBSTSizeRec(node->right, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data < *minValRsubTree)
right_flag = true;
if (min < *minValRsubTree)
*minValRsubTree = min;
if (node->data < *minValRsubTree)
*minValRsubTree = node->data;
if (node->data > *maxValLsubTree)
*maxValLsubTree = node->data;
if(left_flag && right_flag){
if (leftSubtreeSize + rightSubTreeSize + 1 > *maxBSTSize)
*maxBSTSize = (leftSubtreeSize + rightSubTreeSize + 1);
return (leftSubtreeSize + rightSubTreeSize + 1);
}
else{
*isBSTree = false;
return 0;
}
}
int findlargestBSTSize(node* node){
int min = INT_MAX;
int max = INT_MIN;
int largestBSTSize = 0;
bool isBST = false;
findlargestBSTSizeRec(node, &min, &max, &largestBSTSize, &isBST);
return largestBSTSize;
}
int main(){
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The Size of the largest BST is "<<findlargestBSTSize(root);
return 0;
}出力
The Size of the largest BST is 5
以上が指定されたバイナリ ツリー内で最大のバイナリ検索サブツリーを見つける - C++ のエピソード 1の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

