扇形の面積はどれくらいですか?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-08-30 08:33:111071ブラウズ
円セクターは、円セクター/円のセクターとも呼ばれ、2 つの半径間の円弧で囲まれた円の一部です。この領域は 2 つの半径と 1 つの円弧によって境界されます。内接する面積を見つけるには、2 つの半径間の角度を見つける必要があります。総面積は 360 度の角度に等しくなります。角度の面積を求めるには、面積にθ/360を掛けます。これにより、内接部分の面積が得られます。
ここで、θ は 2 つの半径間の角度 (度単位) です。
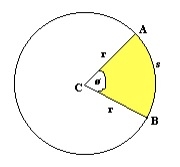
扇形の面積 = π*r*r*(θ/360)。
例
半径 5、角度 60 度の扇形の面積は 13.083 です。
面積 = (3.14*5*5)*(60/360) = 13.03
サンプルコード
デモ
#include <stdio.h>
int main(void) {
int r = 5;
int angle = 60;
float pie = 3.14;
float area = (float)(pie*r*r*angle/360);
printf("The area of sector of a circle of radius %d with an angle of %d is %f", r,angle,area);
return 0;
}出力
The area of sector of a circle of radius 5 with an angle of 60 is 13.083333
以上が扇形の面積はどれくらいですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
声明:
この記事はtutorialspoint.comで複製されています。侵害がある場合は、admin@php.cn までご連絡ください。

