ホームページ >テクノロジー周辺機器 >AI >8 つの一般的な機械学習アルゴリズムの計算複雑さの概要
8 つの一般的な機械学習アルゴリズムの計算複雑さの概要
- 王林転載
- 2023-05-15 21:19:041188ブラウズ
計算の複雑さは、実行時に特定のアルゴリズムによって消費されるコンピューティング リソース (時間とスペース) の尺度です。
計算量は 2 つのカテゴリに分類されます:
1. 時間計算量
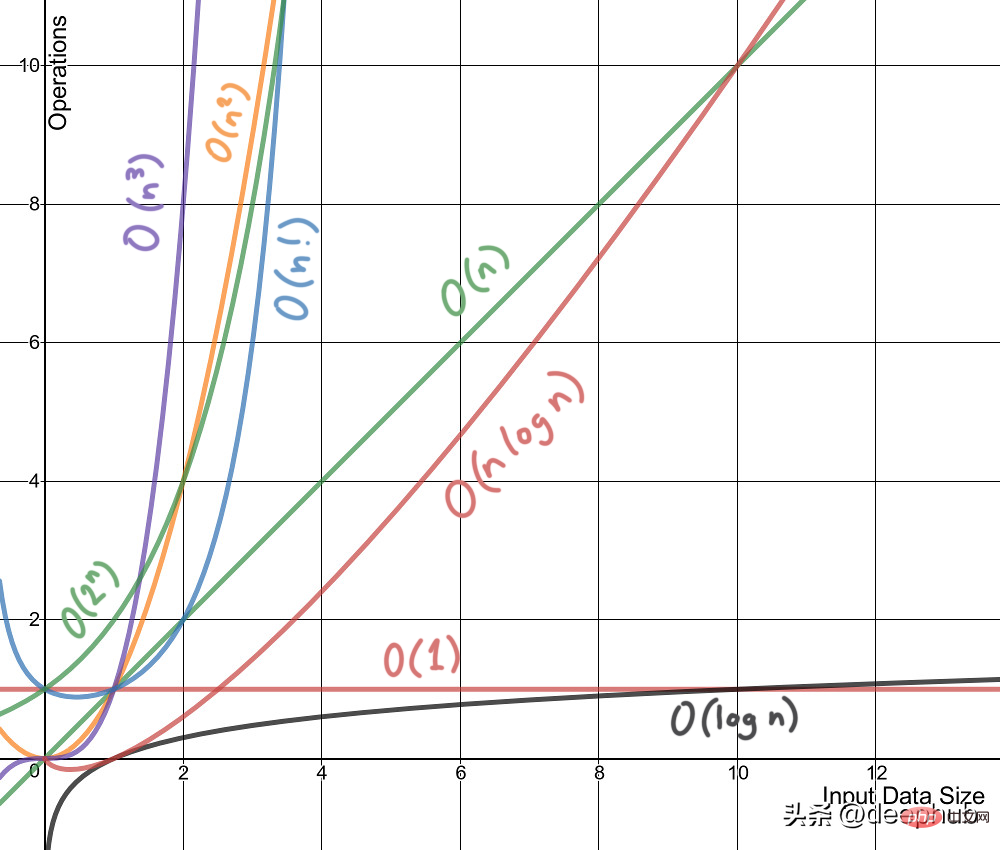
時間計算量は、特定のマシンまたはマシン上で実行されるアルゴリズムやコードの一部の尺度ではありません。状態、かかった時間、時間計算量は一般に、アルゴリズムの実行時間を定性的に記述する関数であり、異なるアルゴリズムを実行せずに比較できるようにする関数です。たとえば、O(n) のアルゴリズムは、成長率が O(n²) よりも小さいため、常に O(n²) よりも優れたパフォーマンスを発揮します。
2. 空間複雑度
時間計算量が関数であるのと同じように、空間複雑度も関数です。概念的には、これは時間の複雑さと同じであり、時間を空間に置き換えるだけです。 Wikipedia では、空間複雑度を次のように定義しています。
アルゴリズムまたはコンピューター プログラムの空間複雑度は、入力としての特徴の数の関数として、計算問題のインスタンスを解くために必要な記憶域の量です。
以下に、いくつかの一般的な機械学習アルゴリズムの計算の複雑さをまとめました。
1. 線形回帰
- n=トレーニング サンプルの数、f = 特徴の数
- トレーニング時間の複雑さ: O(f²n f³)
- 予測時間の複雑さ: O(f)
- 実行時空間の複雑さ: O(f)
2. ロジスティック回帰:
- n = 数値トレーニング サンプルの数、f = 特徴の数
- トレーニング時間の複雑さ: O(f*n)
- 予測時間の複雑さ: O(f)
- 実行時空間の複雑さ: O (f)
3. サポート ベクター マシン:
- n=トレーニング サンプルの数、f=特徴の数、s=サポート ベクターの数
- トレーニング時間の複雑さ: O(n²) から O(n³)、トレーニング時間の複雑さはカーネルによって異なります。
- 予測される時間計算量: O(f) から O(s*f): 線形カーネルは O(f)、RBF、多項式は O(s*f) です。
- 実行時空間の計算量: O(s)
4. 単純ベイズ:
- n=トレーニング サンプルの数、f=特徴の数、c=分類のカテゴリの数
- トレーニング時間の複雑さ: O(n*f*c)
- 予測時間の複雑さ: O(c*f)
- 実行時空間の複雑さ: O(c *f)
5. デシジョン ツリー:
- n=トレーニング サンプルの数、f=特徴の数、d=ツリーの深さ、p=ノードの数
- トレーニング時間の複雑さ: O(n*log(n)*f)
- 予測時間の複雑さ: O(d)
- 実行時空間の複雑さ: O(p)
6. ランダム フォレスト:
- n= トレーニング サンプルの数、f = 特徴の数、k = ツリーの数、p = ツリー内のノードの数、d = ツリーの深さ
- トレーニング時間の複雑さ: O(n*log(n)*f*k)
- 予測時間の複雑さ: O(d*k)
- 実行時空間の複雑さ: O( p*k)
7、K 最近傍:
n=トレーニング サンプルの数、f=特徴の数、k=最近傍の数
Brute:
- トレーニング時間の複雑さ: O(1)
- 予測時間の複雑さ: O(n*f k*f)
- ランタイム空間の複雑さ: O(n *f)
kd ツリー:
- トレーニング時間の複雑さ: O(f*n*log(n))
- 予測時間の複雑さ: O(k*log(n))
- ランタイム空間の複雑さ: O(n*f)
8、K 平均法クラスタリング:
- n= トレーニング サンプルの数、f = 特徴の数、k= クラスターの数、i = 反復数
- トレーニング時間の複雑さ: O(n*f*k *i)
- 実行時空間の複雑さ: O(n*f k*f)
以上が8 つの一般的な機械学習アルゴリズムの計算複雑さの概要の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
声明:
この記事は51cto.comで複製されています。侵害がある場合は、admin@php.cn までご連絡ください。

