Pythonの共通関数でNumPyを使用する方法

1. txt ファイル

(1) 恒等行列

は、主対角上の要素がすべて 1 で、残りの要素が 1 である正方行列です。 0 。

NumPy では、eye 関数を使用して、行列内の 1 の要素の数を指定するパラメータを与えるだけで、このような 2 次元配列を作成できます。

例: 3×3 の配列を作成します:

import numpy as np
I2 = np.eye(3)
print(I2)
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

(2) savetxt 関数を使用してデータをファイルに保存します。もちろん、ファイル名とファイル名を指定する必要があります。保存する配列。

np.savetxt('eye.txt', I2)#创建一个eye.txt文件，用于保存I2的数据

2. CSV ファイル

CSV (Comma-Separated Value) 形式は一般的なファイル形式です。通常、データベース ダンプ ファイルは CSV 形式です。ファイル内の各フィールドはデータベース テーブルの列に対応しており、スプレッドシート ソフトウェア (Microsoft Excel など) で CSV ファイルを処理できます。

注: NumPy のloadtxt 関数は、CSV ファイルを簡単に読み取り、フィールドを自動的にセグメント化し、NumPy 配列にデータをロードできます。

data.csv のデータ内容:

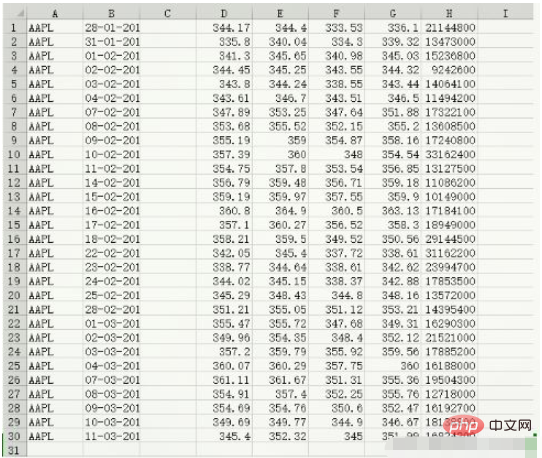
c, v = np.loadtxt('data.csv', delimiter=',', usecols=(6,7), unpack=True)
# usecols的参数为一个元组，以获取第7字段至第8字段的数据
# unpack参数设置为True，意思是分拆存储不同列的数据，即分别将收盘价和成交量的数组赋值给变量c和v
print(c)
[336.1  339.32 345.03 344.32 343.44 346.5  351.88 355.2  358.16 354.54
 356.85 359.18 359.9  363.13 358.3  350.56 338.61 342.62 342.88 348.16
 353.21 349.31 352.12 359.56 360.   355.36 355.76 352.47 346.67 351.99]
print(v)
[21144800. 13473000. 15236800.  9242600. 14064100. 11494200. 17322100.
 13608500. 17240800. 33162400. 13127500. 11086200. 10149000. 17184100.
 18949000. 29144500. 31162200. 23994700. 17853500. 13572000. 14395400.
 16290300. 21521000. 17885200. 16188000. 19504300. 12718000. 16192700.
 18138800. 16824200.]
print(type(c))
print(type(v))
<class &#39;numpy.ndarray&#39;>
<class &#39;numpy.ndarray&#39;>

3.出来高加重平均価格 = Average() function

VWAP の概要: VWAP(出来高加重平均価格 (出来高加重)平均価格）は、金融資産の「平均」価格を表す非常に重要な経済数量です。

特定の価格の取引量が多いほど、その価格の重みは大きくなります。

VWAPとは、取引高を重みとして計算される加重平均であり、アルゴリズム取引でよく使用されます。

vwap = np.average(c,weights=v)
print('成交量加权平均价格vwap =', vwap)
成交量加权平均价格vwap = 350.5895493532009

4. 算術平均関数 = means() 関数

NumPy の平均関数は、配列要素の算術平均を計算できます

print('c数组中元素的算数平均值为： {}'.format(np.mean(c)))
c数组中元素的算数平均值为： 351.0376666666667

5. 時間加重平均価格

TWAP の概要:

経済学では、TWAP (時間加重平均価格、時間加重平均価格) は、もう 1 つの「平均価格」です。インジケータ。 VWAP を計算したので、TWAP も計算しましょう。実は、TWAP というのは単なる変形であり、基本的な考え方は、直近の価格の方が重要であるため、直近の価格をより重視すべきであるということです。最も簡単な方法は、arange 関数を使用して、0 から始まり、順次増加する自然数の列を作成することです (自然数の数が終値の数になります)。もちろん、これは TWAP を計算するための正しい方法であるとは限りません。

t = np.arange(len(c))
print('时间加权平均价格twap=', np.average(c, weights=t))
时间加权平均价格twap= 352.4283218390804

6. 最大値と最小値

h, l = np.loadtxt('data.csv', delimiter=',', usecols=(4,5), unpack=True)
print('h数据为： \n{}'.format(h))
print('-'*10)
print('l数据为： \n{}'.format(l))
h数据为： 
[344.4  340.04 345.65 345.25 344.24 346.7  353.25 355.52 359.   360.
 357.8  359.48 359.97 364.9  360.27 359.5  345.4  344.64 345.15 348.43
 355.05 355.72 354.35 359.79 360.29 361.67 357.4  354.76 349.77 352.32]
----------
l数据为： 
[333.53 334.3  340.98 343.55 338.55 343.51 347.64 352.15 354.87 348.
 353.54 356.71 357.55 360.5  356.52 349.52 337.72 338.61 338.37 344.8
 351.12 347.68 348.4  355.92 357.75 351.31 352.25 350.6  344.9  345.  ]
print('h数据的最大值为： {}'.format(np.max(h)))
print('l数据的最小值为： {}'.format(np.min(l)))
h数据的最大值为： 364.9
l数据的最小值为： 333.53
NumPy中有一个ptp函数可以计算数组的取值范围
该函数返回的是数组元素的最大值和最小值之间的差值
也就是说，返回值等于max(array) - min(array)
print('h数据的最大值-最小值的差值为： \n{}'.format(np.ptp(h)))
print('l数据的最大值-最小值的差值为： \n{}'.format(np.ptp(l)))
h数据的最大值-最小值的差值为： 
24.859999999999957
l数据的最大值-最小值的差值为： 
26.970000000000027

7. 統計分析

中央値: いくつかのしきい値を使用できます。外れ値を削除するために使用されますが、より良い方法、それが中央値です。

変数値をサイズ順に並べて数列を形成します。数列の中央の数値が中央値です。

たとえば、1、2、3、4、5 の 5 つの値がある場合、中央値は中央の数字 3 になります。

m = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
print('m数据中的中位数为： {}'.format(np.median(m)))
m数据中的中位数为： 352.055
# 数组排序后，查找中位数
sorted_m = np.msort(m)
print('m数据排序： \n{}'.format(sorted_m))
N = len(c)
print('m数据中的中位数为： {}'.format((sorted_m[N//2]+sorted_m[(N-1)//2])/2))
m数据排序： 
[336.1  338.61 339.32 342.62 342.88 343.44 344.32 345.03 346.5  346.67
 348.16 349.31 350.56 351.88 351.99 352.12 352.47 353.21 354.54 355.2
 355.36 355.76 356.85 358.16 358.3  359.18 359.56 359.9  360.   363.13]
m数据中的中位数为： 352.055
方差：
方差是指各个数据与所有数据算术平均数的离差平方和除以数据个数所得到的值。
print('variance =', np.var(m))
variance = 50.126517888888884
var_hand = np.mean((m-m.mean())**2)
print('var =', var_hand)
var = 50.126517888888884

注: 標本分散と母集団分散の計算の違い。母集団の分散は偏差の二乗和をデータ数で割ったものですが、標本分散は偏差の二乗和を標本データの数から 1 を引いたもので、標本データの数から 1 を引いたものです (つまり、n- 1) を自由度といいます。この違いの理由は、サンプル分散が不偏推定量であることを保証するためです。

8. 株式リターン

学術文献では、終値の分析は多くの場合、株式リターンと対数リターンに基づいています。

単純収益率は、隣接する 2 つの価格間の変化率を指しますが、対数収益率は、すべての価格の対数を取った後の 2 つの価格の差を指します。
対数については高校で習いましたが、「a」の対数から「b」の対数を引いたものは、「aをbで割った」の対数に等しいです。したがって、ログリターンは価格の変化率を測定するためにも使用できます。

収益率は比率であるため、たとえば米ドルを米ドルで割ったものであるため(他の通貨単位でも構いません)、無次元であることに注意してください。

つまり、投資家が最も関心があるのは収益率の分散または標準偏差です。これは投資リスクの大きさを表すためです。

(1) まず、単純な収益率を計算してみましょう。 NumPy の diff 関数は、隣接する配列要素間の差分で構成される配列を返すことができます。これは微分積分に似ています。利回りを計算するには、前日の価格を差で割る必要もあります。ただし、diff によって返される配列には、終値配列よりも 1 つの要素が少ないことに注意してください。 returns = np.diff(arr)/arr[:-1]

終値配列の最後の値を除数として使用しないことに注意してください。次に、std 関数を使用して標準偏差を計算します。

print ("Standard deviation =", np.std(returns))

(2) 対数リターンの計算はさらに簡単です。まず log 関数を使用して各終値の対数を取得し、次にその結果に対して diff 関数を使用します。

logreturns = np.diff( np.log(c) )

一般に、入力配列をチェックして、ゼロや負の数が含まれていないことを確認する必要があります。そうしないと、エラー メッセージが表示されます。ただし、この例では株価は常にプラスであるため、チェックを省略できます。

(3) 私たちは、どの取引日がプラスのリターンをもたらすかに非常に興味を持っていると思われます。

前の手順を完了したら、これを行うには where 関数を使用するだけです。 where関数は、指定された条件に従って、条件を満たすすべての配列要素のインデックス値を返すことができます。

次のコードを入力してください:

posretindices = np.where(returns > 0)
print "Indices with positive returns", posretindices
即可输出该数组中所有正值元素的索引。
Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28]),)

(4) 在投资学中，波动率（volatility）是对价格变动的一种度量。历史波动率可以根据历史价格数据计算得出。计算历史波动率（如年波动率或月波动率）时，需要用到对数收益率。年波动率等于对数收益率的标准差除以其均值，再除以交易日倒数的平方根，通常交易日取252天。用std和mean函数来计算

代码如下所示：

annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility / np.sqrt(1./252.)

(5) sqrt函数中的除法运算。在Python中，整数的除法和浮点数的除法运算机制不同(python3已修改该功能)，我们必须使用浮点数才能得到正确的结果。与计算年波动率的方法类似，计算月波动率如下：

annual_volatility * np.sqrt(1./12.)

c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)

returns = np.diff(c)/c[:-1]
print('returns的标准差： {}'.format(np.std(returns)))
logreturns = np.diff(np.log(c))
posretindices = np.where(returns>0)
print('retruns中元素为正数的位置： \n{}'.format(posretindices))
annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility/np.sqrt(1/252)
print('每年波动率: {}'.format(annual_volatility))
print('每月波动率：{}'.format(annual_volatility*np.sqrt(1/12)))
returns的标准差： 0.012922134436826306
retruns中元素为正数的位置： 
(array([ 0,  1,  4,  5,  6,  7,  9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23,
       25, 28], dtype=int64),)
每年波动率: 129.27478991115132
每月波动率：37.318417377317765

以上がPythonの共通関数でNumPyを使用する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。