カーネル手法を超えた量子機械学習、量子学習モデルの統一フレームワーク

パラメータ化された量子回路に基づく機械学習アルゴリズムは、ノイズの多い量子コンピューターでの短期的なアプリケーションの主な候補です。この方向に向けて、さまざまなタイプの量子機械学習モデルが導入され、広範囲に研究されています。ただし、これらのモデルが相互に、また古典的なモデルとどのように比較されるかについての理解は依然として限られています。

最近、オーストリアのインスブルック大学の研究チームは、パラメータ化された量子回路に基づいてすべての標準モデルを捉える構築的なフレームワーク、つまり線形量子モデルを特定しました。

研究者らは、量子情報理論のツールを使用して、データ再アップロード回路を量子ヒルベルト空間の線形モデルのより単純な図に効率的にマッピングする方法を示しています。さらに、これらのモデルの実験に関連したリソース要件は、量子ビットの数と学習する必要があるデータの量の観点から分析されます。古典的な機械学習に基づく最近の結果は、線形量子モデルが特定の学習タスクを解決するにはデータ再アップロード モデルよりも多くの量子ビットを使用する必要がある一方、カーネル手法ではより多くのデータ ポイントも必要であることを示しています。その結果、量子機械学習モデルについてのより包括的な理解が得られるとともに、さまざまなモデルと NISQ 制約との互換性についての洞察が得られます。

研究のタイトルは「カーネル手法を超えた量子機械学習」で、2023 年 1 月 31 日に「Nature Communications」に掲載されました。 。

紙のリンク: https: / /www.nature.com/articles/s41467-023-36159-y

現在の騒々しい中間レベル量子 (NISQ) 時代では、わずかなハードウェア制約と互換性のある有用な量子アルゴリズムを構築するいくつかの方法が提案されています。これらの手法のほとんどには、特定の計算タスクを解決するために古典的な方法で最適化された Ansatz 量子回路の仕様が含まれています。化学における変分量子署名ソルバーや量子近似最適化アルゴリズムの変形に加え、そのようなパラメータ化された量子回路に基づく機械学習手法は、量子の利点を生み出すための最も有望な実用的なアプリケーションの 1 つです。

カーネル メソッドは、パターン認識アルゴリズムの一種です。その目的は、一連のデータ内の相互関係を見つけて学習することです。カーネル法は、非線形パターン解析の問題を解決する効果的な方法です。その中心的なアイデアは、まず、非線形マッピングを通じて元のデータを適切な高次元特徴空間に埋め込み、次に、一般線形学習器を使用して新しい解析モードを実行することです。そして宇宙での処理。

これまでの研究では、いくつかの量子モデルと古典的な機械学習のカーネル手法の間の接続を利用することにより、この方向で大きな進歩を遂げました。実際、多くの量子モデルは、高次元ヒルベルト空間でデータをエンコードし、この特徴空間で評価された内積のみを使用してデータのプロパティをモデル化することによって動作します。これは核法も同様です。

この類似性に基づいて、特定の量子エンコーディングを使用して 2 種類のモデルを定義できます: (a) 明示的な量子モデル。データ ポイントは変数に従ってエンコードされます。ラベルを指定します 測定は個別のオブザーバブルに対して行われます; または (b) 暗黙的なカーネル モデルでは、エンコードされたデータ ポイントの加重内積がラベルの割り当てに使用されます。量子機械学習の文献では、陰的モデルに重点が置かれています。

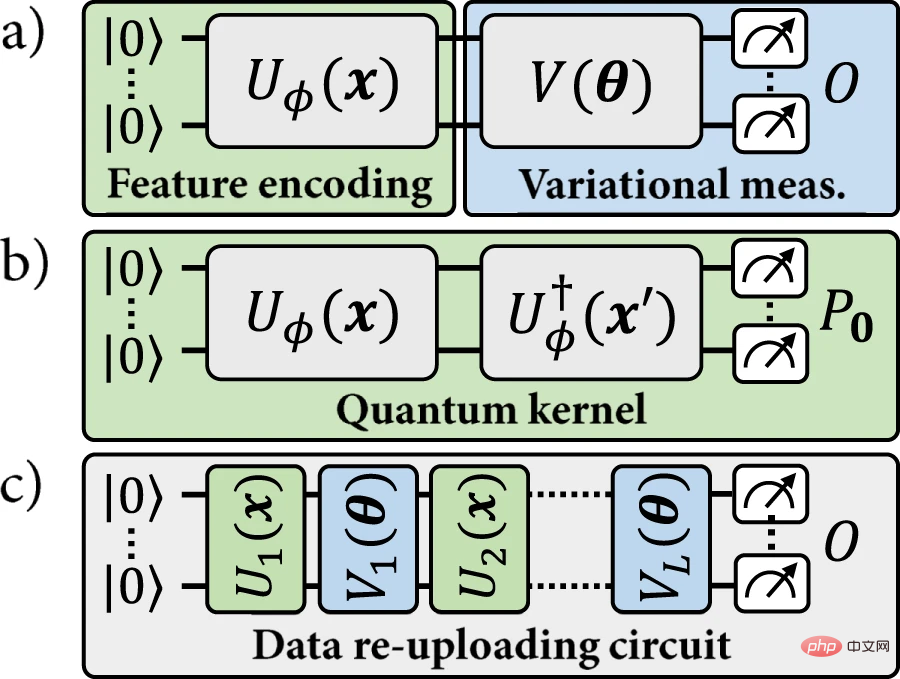
# 図 1: この研究で研究された量子機械学習モデル。 (出典: 論文)

#最近、いわゆるデータ再アップロード モデルが進展しています。データ再アップロード モデルは、明示的モデルの一般化として見ることができます。ただし、この一般化では、特定のデータ点 x が固定エンコード点 ρ(x) に対応しなくなるため、陰的モデルとの対応関係も崩れます。データ再アップロード モデルは厳密には明示的モデルよりも一般的であり、カーネル モデル パラダイムと互換性がありません。これまでのところ、カーネル メソッドを保証したデータ再アップロード モデルから何らかの利点が得られるかどうかは未解決の問題のままです。

この研究では、研究者らは、明示的、暗黙的、およびデータ再アップロード量子モデルのための統一フレームワークを導入します。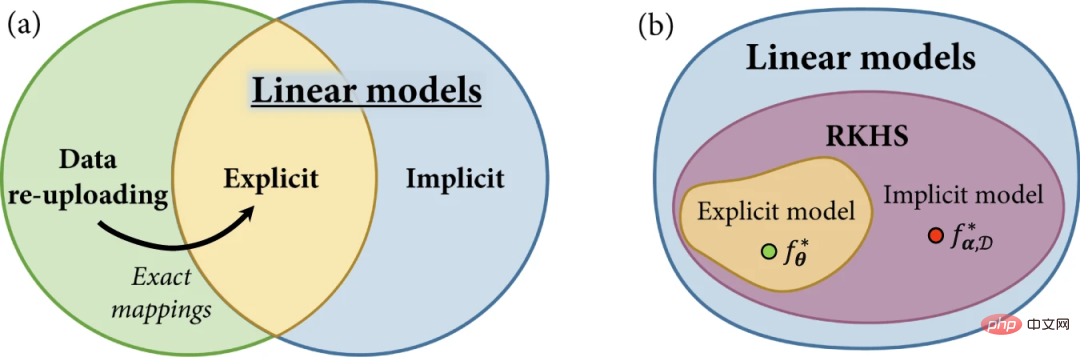

# 図 2: 量子機械学習のモデル ファミリ。 (出典: 論文)

量子学習モデルの統合フレームワーク

最初に線形量子モデルの概念を確認し、量子特徴空間の観点から線形モデルを定義します。明示的モデルと暗黙的モデルについて説明します。次に、データ再アップロード モデルが提示され、明示的モデルの一般化として定義されているものの、より大きなヒルベルト空間の線形モデルによっても実装できることが示されています。

線形量子モデル

以下の図は、データの再アップロードから明示的モデルへのマッピングを実装する方法を視覚的に説明するための例示的な構造を示しています。

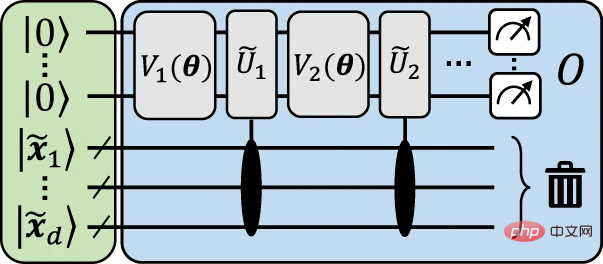
# 図 3: データ再アップロード回路を近似する明示的なモデルの例。 (出典: 論文)

#この構造の背後にある一般的な考え方は、入力データ x を補助量子ビットに有限精度でエンコードし、データ非依存性を使用して再利用できるようにすることです。ユニタリーは、データ エンコーディング ゲートを近似するために使用されます。

次にメイン構造に移ります。これにより、データが再アップロードされ、明示的モデル間の正確なマッピングが行われます。ここでは、前の構造と同様の考え方に基づいて、入力データが補助量子ビットでエンコードされ、その後、データに依存しない操作を使用してエンコード ゲートが作業量子ビットに実装されます。ここでの違いは、測定ベースの量子コンピューティングの一種であるゲート テレポーテーションを使用して、補助量子ビットに直接エンコード ゲートを実装し、必要に応じてそれらを作業量子ビットに (エンタングルメント測定を介して) テレポートして戻すことです。

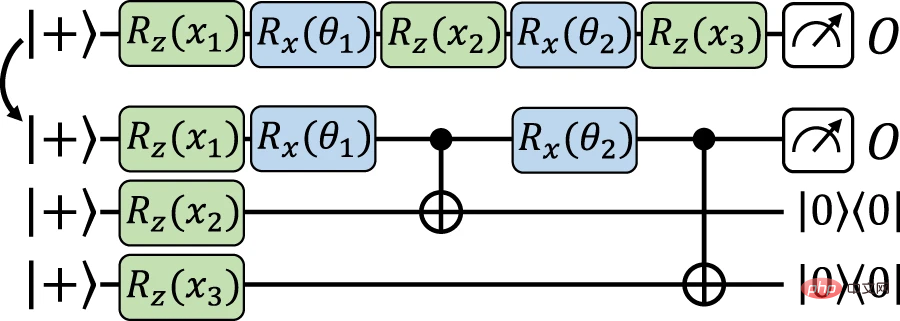
図 4: ゲート テレポーテーションを使用してモデルをデータから同等の明示的なモデルに再アップロードする 正確なマッピング。 (出典: 論文)

#研究者らは、線形量子モデルが陽的モデルと陰的モデルだけでなく、データ再アップロード回路も記述できることを実証しました。より具体的には、データ再アップロード モデルの任意の仮説クラスを、明示的モデルの同等のクラス、つまり、制限されたオブザーバブル ファミリを持つ線形モデルにマッピングできます。

研究者らはその後、暗黙的モデルに対する明示的モデルとデータ再アップロード モデルの利点をより厳密に分析しました。この例では、学習タスクを解決する際の量子モデルの効率が、量子ビットの数と、自明ではない予想損失を達成するために必要なトレーニング セットのサイズによって定量化されます。興味深い学習タスクは、奇数関数と偶数関数を学習することです。

# 図 5: 分離することを学ぶ。 (出典: 論文)

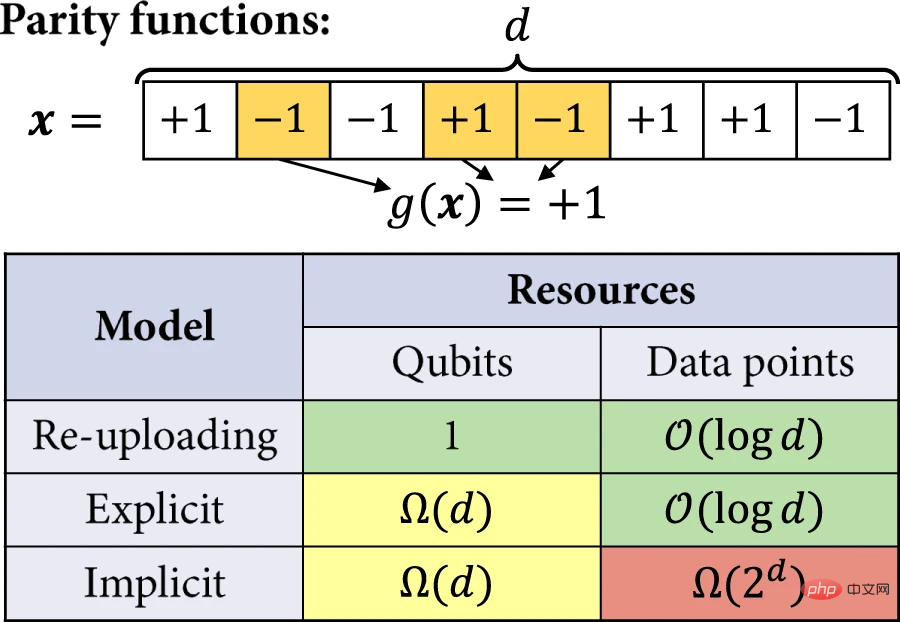
核手法を超えた量子の利点

量子機械学習における主な課題は、この研究で議論されている量子手法が学習に役立つことを示すことです。 (標準的な) 古典的な方法よりも優れた利点を実現できます。

この研究では、Google Quantum Artificial Intelligence の Huang ら (

https://www.php.cn/link/4dfd2a142d36707f8043c40ce0746761 ) ターゲット関数自体を研究することをお勧めします量子モデル生成のための (明示的な) 学習タスクによる。

Huang らと同様に、研究者らは、fashion-MNIST データセットからの入力データを使用して回帰タスクを実行しました。各例は 28x28 のグレースケール画像でした。

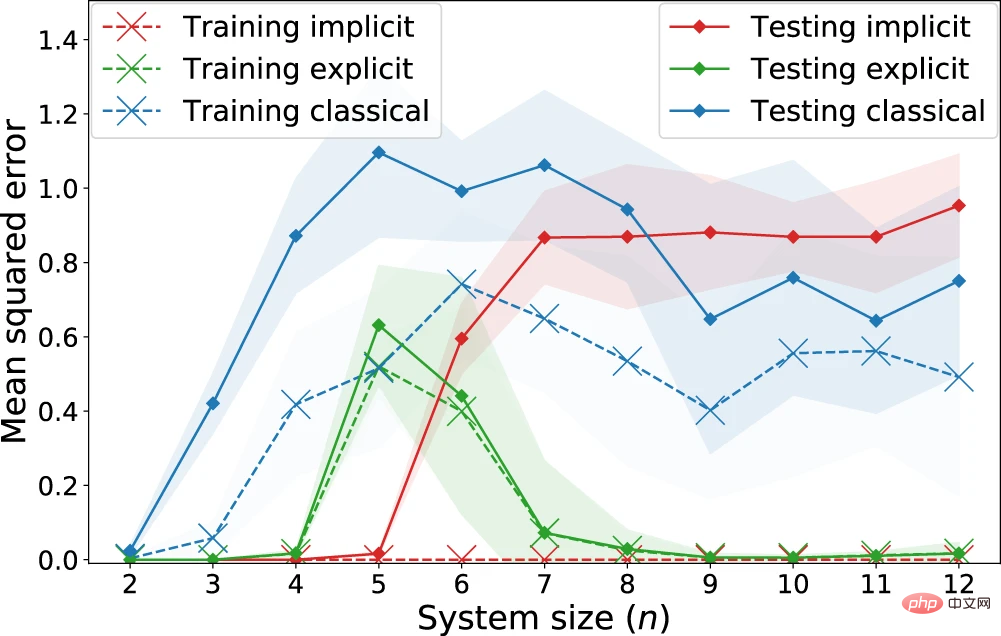
図 6: 「量子カスタマイズ」学習タスクにおける陽的モデル、陰的モデル、古典的モデルのパフォーマンスパフォーマンスへ。 (出典: 論文)

#観察: 陰的モデルは、陽的モデルよりも体系的に低い学習損失を達成します。特に非正規化損失の場合、陰的モデルは学習損失 0 を達成します。一方、期待される損失を表すテスト損失に関しては、n = 7 量子ビットから明確な分離があり、古典的モデルが陰的モデルと競合するパフォーマンスを持ち始めますが、陽的モデルは明らかに両方を上回っています。 。これは、明示的 (またはデータの再アップロード) モデルによってより優れた学習パフォーマンスが隠蔽される可能性があるため、量子優位性の存在を古典モデルと量子カーネル手法との比較のみによって評価すべきではないことを示唆しています。

これらの結果により、量子機械学習の分野についてより包括的な理解が得られ、NISQ メカニズムで実際的な学習上の利点を実現するためのモデルの種類についての視野が広がりました。

研究者らは、異なる量子モデル間に指数関数的な学習分離が存在することを証明するという学習タスクは、奇数関数と偶数関数に基づいており、機械にとって実際に興味深い概念クラスではないと考えています。学ぶ。ただし、下限の結果は、大次元の概念クラス (つまり、多くの直交関数で構成される) を含む他の学習タスクに拡張することもできます。

量子カーネル手法では、必然的にこの次元に線形にスケールする多くのデータ ポイントが必要になります。結果に示されているように、データ再アップロード回路と明示的モデルの制限された式の柔軟性が必要です。多くのリソースを節約する機能。これらのモデルを、いつ、どのようにして、当面の機械学習タスクに合わせて調整できるかを探ることは、依然として興味深い研究方向です。

以上がカーネル手法を超えた量子機械学習、量子学習モデルの統一フレームワークの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。