Pythonの組み込みヒープを実装する方法
- WBOY転載
- 2023-04-28 20:40:131247ブラウズ
1. はじめに
プライオリティ キューとも呼ばれるヒープは完全なバイナリ ツリーであり、その各親ノードの値は、すべての子ノード (の値) 以下である必要があります。配列を使用して実装します。ゼロから数えて、すべての k に対して、 heap[k] があります。比較のために、存在しない要素は無限であるとみなします。ヒープの最も興味深い特徴は、最小の要素が常にルート ノード heap[0] にあることです。
Python のヒープは一般的に最小ヒープであり、多くの教科書の内容とは異なります。ほとんどの教科書では最大ヒープが使用されます。ヒープの表現方法により、ヒープは上から下に格納されます。左から右へ、これは多くの教科書の内容とは異なります。リストは非常に似ているため、ヒープを作成するには、[] に初期化されたリストを使用するか、関数 heapify( を使用してリストをヒープに変換できます) ）。以下は Python のヒープに対する関連する操作です。このことから、Python は実際にヒープをリストとして扱っていることがわかります。
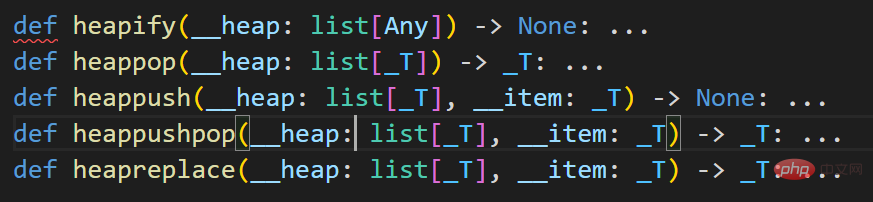
2. ヒープ関連の操作
heapq.heappush(heap, item)
アイテムの値をヒープに追加して保持します。ヒープの不変性。 Python の最小ヒープ機能に従って、関連する要素が自動的に交換されるため、ヒープのルート ノード要素が子ノード要素よりも大きくなることはありません。
元のデータはヒープです
import heapq h = [1, 2, 3, 5, 7] heapq.heappush(h, 2) print(h) #输出 [1, 2, 2, 5, 7, 3]
操作プロセスは次のとおりです:
1. 以下は初期状態
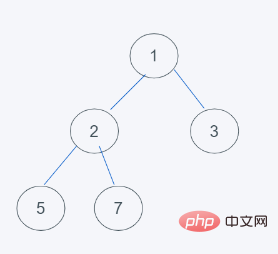
2. 2要素追加後
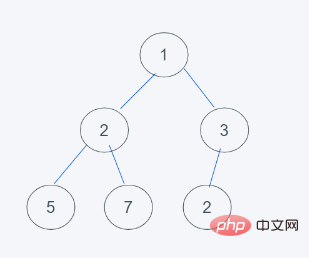
#3. 最小値の特性を満たしていないためheap の場合、3
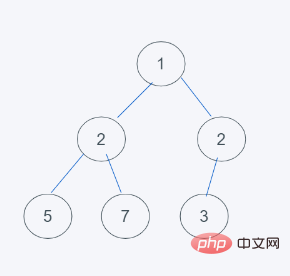
4 と交換されます。最小ヒープの特性に従って交換が終了するため、結果は [1, 2, 3, 5] となります。 , 7, 3]
元のヒープにないデータがあります
import heapq h = [5, 2, 1, 4, 7] heapq.heappush(h, 2) print(h) #输出 [5, 2, 1, 4, 7, 2]
プッシュ操作を実行すると要素が存在しないことがわかります。ヒープ内では、リストの append メソッドに従って要素がデフォルトで追加されます
heapq.heappop( heap)
ヒープを変更せずに、ヒープの最小の要素をポップして返します。 。ヒープが空の場合は、IndexError をスローします。 heap[0] を使用すると、ポップせずに最小の要素のみにアクセスできます。
元のデータはヒープです
import heapq h = [1, 2, 3, 5, 7] heapq.heappop(h) print(h) #输出 [2, 5, 3, 7]
操作プロセスは次のとおりです:
1.初期状態
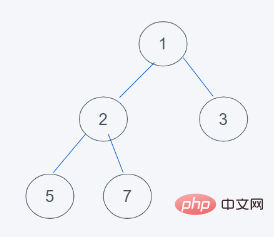
2. ヒープの先頭要素が削除され、最後の要素がヒープの先頭に移動します
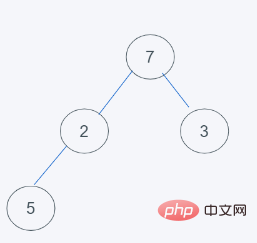
3. 要素は Python の最小ヒープの特性に従って交換されます。7>2 では 7 と 2
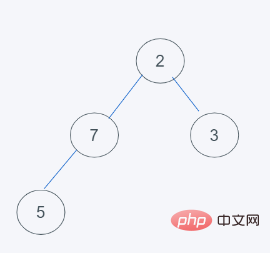
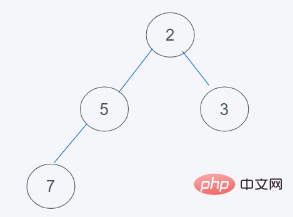
元のデータはヒープではありません
import heapq h = [5, 2, 1, 4, 7] heapq.heappop(h) print(h) [1, 2, 7, 4]
操作プロセスは次のとおりです:
1. 初期状態明らかにヒープの性質に準拠していません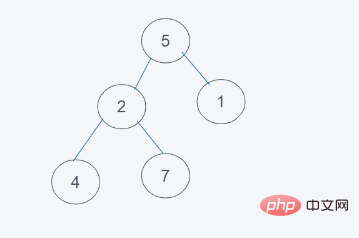
に再配置します
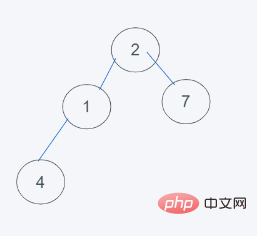
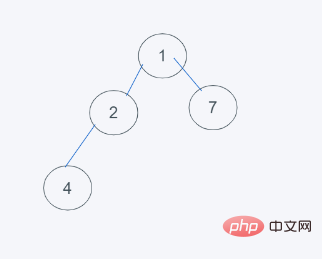
#heapq.heappushpop(heap, item)
アイテムをヒープに入れてから取り出して、ヒープの最小要素。この組み合わせた操作は、最初に heappush() を呼び出してから heappop() を呼び出すよりも効率的に実行されます。ポップされた要素はヒープの先頭または末尾にある必要があることに注意してください。つまり、要素が挿入され、最小の要素が比較される場合、常にヒープの先頭の要素が比較されます。挿入された要素の場合、ヒープの最上位要素以上である場合、ヒープは変更されません。挿入された要素がヒープの最上位要素より小さい場合、ヒープは Python ヒープの最小ヒープ特性に従って処理されます。
元データはヒープです
import heapq h = [1, 2, 3, 5, 7] min_data = heapq.heappushpop(h, 2) print(min_data) print(h) #输出 1 [2, 2, 3, 5, 7]操作手順は以下の通りです
1. 初期状態
##2.要素 2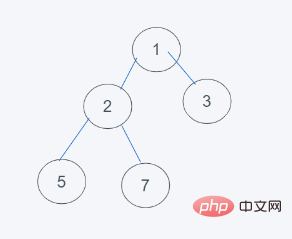
3.删除最小元素，刚好是堆顶元素1，并使用末尾元素2代替
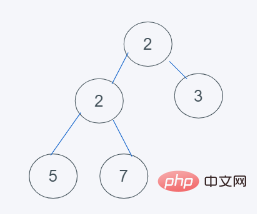
4.符合要求，即结果为[2, 2, 3, 5, 7]
原有数据不是堆
h = [5, 2, 1, 4, 7] min_data = heapq.heappushpop(h, 2) print(min_data) print(h) min_data = heapq.heappushpop(h, 6) print(min_data) print(h) #输出 2 [5, 2, 1, 4, 7] 5 [1, 2, 6, 4, 7]
对于插入元素6的操作过程如下
1.初始状态
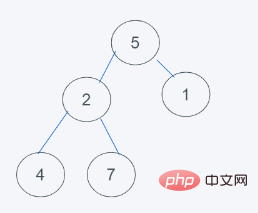
2.插入元素6之后
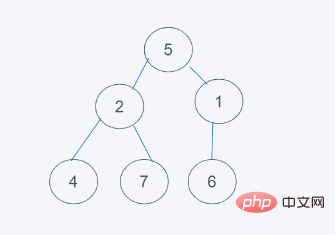
3.发现元素6大于堆顶元素5，弹出堆顶元素5，由堆尾元素6替换
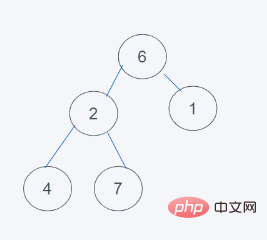
4.依据python的最小堆特性，元素6>元素1且元素6>元素2，但元素2>元素1， 交换6与1
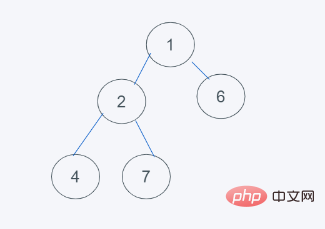
5.符合要求，则结果为[1, 2, 6, 4, 7]
由结果可以看出，当插入元素小于堆顶元素时，则堆不会发生改变，当插入元素大于堆顶元素时，则堆依据python堆的最小堆特性处理。
heapq.heapify(x)
将列表转换为堆。
h = [1, 2, 3, 5, 7] heapq.heapify(h) print(h) h = [5, 2, 1, 4, 7] heapq.heapify(h) print(h) #输出 [1, 2, 3, 5, 7] [1, 2, 5, 4, 7]
会自动将列表依据python最小堆特性进行重新排列。
heapq.heapreplace(heap, item)
弹出并返回最小的元素，并且添加一个新元素item，这个单步骤操作比heappop()加heappush() 更高效。适用于堆元素数量固定的情况。
返回的值可能会比添加的 item 更大。 如果不希望如此，可考虑改用heappushpop()。 它的 push/pop 组合会返回两个值中较小的一个，将较大的值留在堆中。
import heapq h = [1, 2, 3, 5, 7] heapq.heapreplace(h, 6) print(h) h = [5, 2, 1, 4, 7] heapq.heapreplace(h, 6) print(h) #输出 [2, 5, 3, 6, 7] [1, 2, 6, 4, 7]
原有数据是堆
对于插入元素6的操作过程如下：
1.初始状态
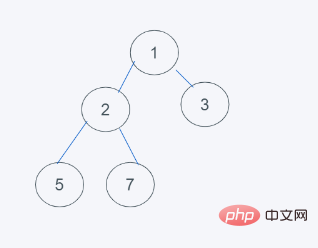
2.弹出最小元素，只能弹出堆顶或者堆尾的元素，很明显，最小元素是1，弹出1，插入元素是6，代替堆顶元素
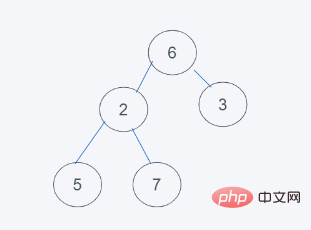
3.依据python堆的最小堆特性，6>2,交换6与2
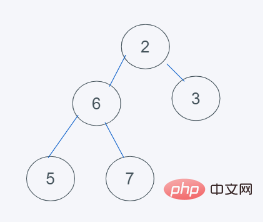
4.依据python堆的最小堆特性，6>5,交换6与5
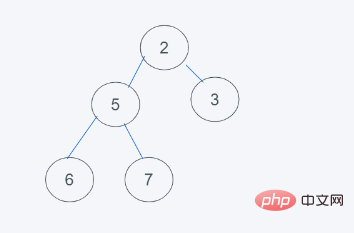
5.符合要求，则结果为[2, 5, 3, 6 ,7]
原有数据不是堆
对于插入元素6的操作过程如下：
1.初始状态
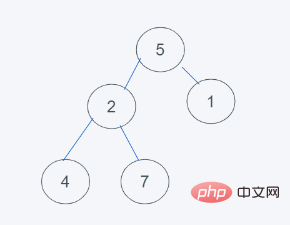
2.对于数据不为堆的情况下，默认移除第一个元素，这里就是元素5，然后插入元素6到堆顶
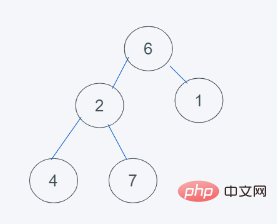
3.依据python的最小堆特性，元素6>1,交换元素6与1
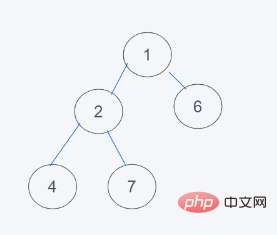
4.符合要求，即结果为[1, 2, 6, 4, 7
heapq.merge(*iterables, key=None, reverse=False)
将多个已排序的输入合并为一个已排序的输出（例如，合并来自多个日志文件的带时间戳的条目）。 返回已排序值的 iterator。注意需要是已排序完成的可迭代对象（默认为从小到大排序），当reverse为True时，则为从大到小排序。
heapq.nlargest(n, iterable, key=None)
从 iterable 所定义的数据集中返回前 n 个最大元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。
等价于: sorted(iterable, key=key, reverse=True)[:n]。
import time
import heapq
h = [1, 2, 3, 5, 7]
size = 1000000
start = time.time()
print(heapq.nlargest(3, h))
for i in range(size):
heapq.nlargest(3, h)
print(time.time() - start)
start = time.time()
print(sorted(h, reverse=True)[:3:])
for i in range(size):
sorted(h, reverse=True)[:3:]
print(time.time() - start)
#输出
[7, 5, 3]
1.6576552391052246
[7, 5, 3]
0.2772986888885498
[7, 5, 4]由上述结构可见，heapq.nlargest与sorted(iterable, key=key, reverse=False)[:n]功能是类似的，但是性能方面还是sorted较为快速。
heapq.nsmallest(n, iterable, key=None)
从 iterable 所定义的数据集中返回前 n 个最小元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。 等价于: sorted(iterable, key=key)[:n]。
import time
import heapq
h = [1, 2, 3, 5, 7]
size = 1000000
start = time.time()
print(heapq.nsmallest(3, h))
for i in range(size):
heapq.nsmallest(2, h)
print(time.time() - start)
start = time.time()
print(sorted(h, reverse=False)[:3:])
for i in range(size):
sorted(h, reverse=False)[:2:]
print(time.time() - start)
#输出
[1, 2, 3]
1.1738648414611816
[1, 2, 3]
0.2871997356414795由上述结果可见，sorted的性能比后面两个函数都要好，但如果只是返回最大的或者最小的一个元素，则使用max和min最好。
3.堆排序
由于在python中堆的特性是最小堆，堆顶的元素始终是最小的，可以将序列转换成堆之后，再使用pop弹出堆顶元素来实现从小到大排序。具体实现如下：
from heapq import heappush, heappop, heapify
def heapsort(iterable):
h = []
for value in iterable:
heappush(h, value)
return [heappop(h) for i in range(len(h))]
def heapsort2(iterable):
heapify(iterable)
return [heappop(iterable) for i in range(len(iterable))]
data = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
print(heapsort(data))
print(heapsort2(data))
#输出
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]4.堆中元素可以是元组形式，主要用于任务优先级
from heapq import heappush, heappop h = [] heappush(h, (5, 'write code')) heappush(h, (7, 'release product')) heappush(h, (1, 'write spec')) heappush(h, (3, 'create tests')) print(h) print(heappop(h)) [(1, 'write spec'), (3, 'create tests'), (5, 'write code'), (7, 'release product')] (1, 'write spec')
上述操作流程如下：
1.当进行第一次push(5, ‘write code’)时
2.当进行第二次push(7, ‘release product’)时，符合堆的要求
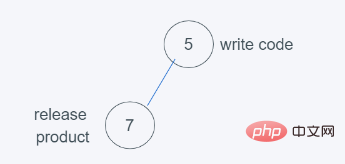
3.当进行第三次push(1, ‘write spec’)时，
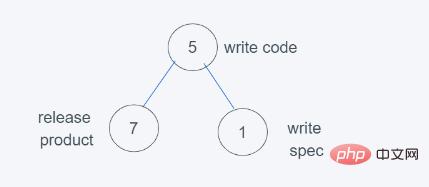
4.依据python的堆的最小堆特性，5>1 ，交换5和1
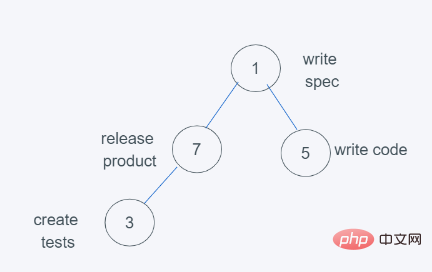
5.当进行最后依次push(3, ‘create tests’)时
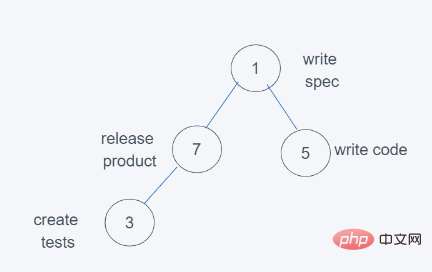
6.依据python堆的最小堆特性，7>3，交换7与3
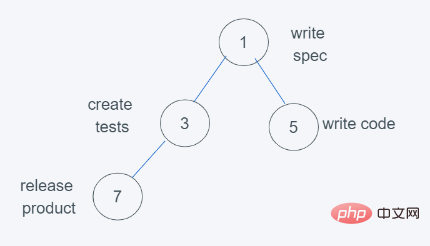
7.符合要求，因此结果为[(1, ‘write spec’), (3, ‘create tests’), (5, ‘write code’), (7, ‘release product’)],弹出元素则是堆顶元素，数字越小，优先级越大。
以上がPythonの組み込みヒープを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。