よく使用される損失関数と Python の実装例

損失関数とは何ですか?

損失関数は、モデルとデータの間の適合度を測定するアルゴリズムです。損失関数は、実際の測定値と予測値の差を測定する方法です。損失関数の値が大きいほど予測は不正確であり、損失関数の値が小さいほど予測は真の値に近づきます。損失関数は、個々の観測値 (データ ポイント) ごとに計算されます。すべての損失関数の値を平均する関数はコスト関数と呼ばれますが、損失関数は 1 つのサンプルに対するものであり、コスト関数はすべてのサンプルに対するものであると理解すると簡単です。

損失関数とメトリクス

一部の損失関数は、評価メトリクスとしても使用できます。ただし、損失関数と指標には異なる目的があります。メトリクスは最終モデルを評価し、さまざまなモデルのパフォーマンスを比較するために使用されますが、損失関数は、作成中のモデルのオプティマイザーとしてモデル構築フェーズ中に使用されます。損失関数は、誤差を最小限に抑える方法についてモデルをガイドします。

つまり、損失関数はモデルがどのようにトレーニングされるかを認識し、測定インデックスはモデルのパフォーマンスを説明します。

損失関数を使用する理由は何ですか?

理由は損失関数の測定値は予測値と実際の値の差であるため、モデルのトレーニング (通常の勾配降下法) の際にモデルの改善のガイドとして使用できます。モデルを構築する過程で、特徴の重みが変化し、予測が良くなったり悪くなったりした場合、損失関数を使用して、モデル内の特徴の重みを変更する必要があるかどうか、および方向を変更する必要があるかを判断する必要があります。変化。

機械学習では、解決しようとしている問題の種類、データの品質と分布、使用するアルゴリズムに応じて、さまざまな損失関数を使用できます。次の図は、私たちが持っている 10 個の損失関数を示しています。コンパイルされた一般的な損失関数:

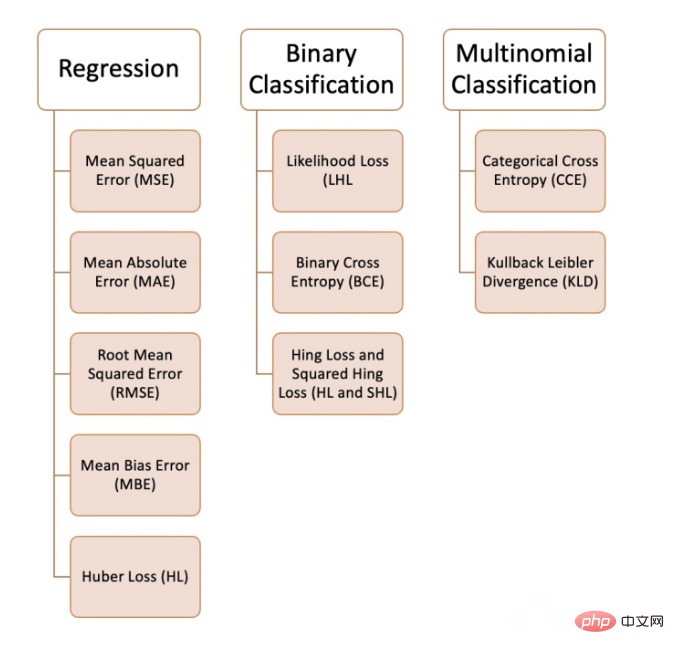
回帰問題

1. 平均二乗誤差 (MSE)

平均二乗誤差は、すべての予測値を指します。と真の値を求め、それらを平均します。回帰問題でよく使用されます。

def MSE (y, y_predicted):
 sq_error = (y_predicted - y) ** 2
 sum_sq_error = np.sum(sq_error)
 mse = sum_sq_error/y.size
 return mse

2. 平均絶対誤差 (MAE)

は、予測値と真の値の間の絶対差の平均として計算されます。データに外れ値がある場合、これは平均二乗誤差よりも優れた測定値となります。

def MAE (y, y_predicted):
 error = y_predicted - y
 absolute_error = np.absolute(error)
 total_absolute_error = np.sum(absolute_error)
 mae = total_absolute_error/y.size
 return mae

3. 二乗平均平方根誤差 (RMSE)

この損失関数は、平均二乗誤差の平方根です。これは、より大きなエラーを罰したくない場合に理想的なアプローチです。

def RMSE (y, y_predicted):
 sq_error = (y_predicted - y) ** 2
 total_sq_error = np.sum(sq_error)
 mse = total_sq_error/y.size
 rmse = math.sqrt(mse)
 return rmse

4. 平均偏差誤差 (MBE)

は平均絶対誤差と似ていますが、絶対値を求めません。この損失関数の欠点は、負の誤差と正の誤差が互いに打ち消し合う可能性があることであるため、研究者が誤差が一方向にしか進まないことがわかっている場合に適用することをお勧めします。

def MBE (y, y_predicted):
 error = y_predicted -y
 total_error = np.sum(error)
 mbe = total_error/y.size
 return mbe

5. フーバー損失

フーバー損失関数は、平均絶対誤差 (MAE) と平均二乗誤差 (MSE) の利点を組み合わせたものです。これは、ハバー損失が 2 つの分岐を持つ関数であるためです。 1 つのブランチは期待値と一致する MAE に適用され、もう 1 つのブランチは外れ値に適用されます。ハバー損失の一般的な機能は次のとおりです:

#ここで

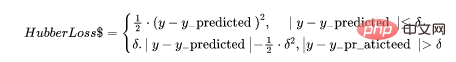
def hubber_loss (y, y_predicted, delta)
 delta = 1.35 * MAE
 y_size = y.size
 total_error = 0
 for i in range (y_size):
erro = np.absolute(y_predicted[i] - y[i])
if error < delta:
 hubber_error = (error * error) / 2
else:
 hubber_error = (delta * error) / (0.5 * (delta * delta))
total_error += hubber_error
 total_hubber_error = total_error/y.size
 return total_hubber_error

二項分類

6. 最尤損失 (尤度損失/LHL)

この損失関数は主に二項分類問題に使用されます。各予測値の確率を乗算して損失値を取得し、関連するコスト関数はすべての観測値の平均となります。クラスが [0] または [1] である二項分類の次の例を考えてみましょう。出力確率が 0.5 以上の場合、予測クラスは [1]、それ以外の場合は [0] になります。出力確率の例は次のとおりです:

[0.3 , 0.7 , 0.8 , 0.5 , 0.6 , 0.4]

対応する予測クラス:

[0 , 1 , 1 , 1 , 1 , 0]

、実際のクラス:

[0 , 1 , 1 , 0 , 1 , 0]

これで、実際のクラスと出力確率が決まります。損失の計算に使用されます。真のクラスが [1] の場合は出力確率を使用し、真のクラスが [0] の場合は 1 の確率を使用します:

((1–0.3)+0.7+0.8+(1–0.5)+0.6+(1–0.4)) / 6 = 0.65

Python コードは次のとおりです:

def LHL (y, y_predicted):
 likelihood_loss = (y * y_predicted) + ((1-y) * (y_predicted))
 total_likelihood_loss = np.sum(likelihood_loss)
 lhl = - total_likelihood_loss / y.size
 return lhl

7. バイナリ クロスオーバー エントロピー (BCE)

この関数は、対数尤度損失を修正したものです。一連の数値を積み重ねると、信頼性は高いが不正確な予測にペナルティが生じる可能性があります。バイナリ クロスエントロピー損失関数の一般式は次のとおりです。

上記の例の値を引き続き使用しましょう。

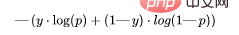
出力確率 = [0.3, 0.7, 0.8, 0.5, 0.6, 0.4]
1. ## 実際のクラス = [0, 1, 1, 0, 1, 0]
2. #(0 . log (0.3) (1–0) . log (1–0.3)) = 0.155

(1 . log(0.7) (1–1) . log (0.3) ) = 0.155
• (1 . log(0.8) (1–1) . log (0.2)) = 0.097
• (0 . log (0.5) (1–0) . log ( 1–0.5) ) = 0.301
• (1 . log(0.6) (1–1) . log (0.4)) = 0.222
• (0 . log (0.4) (1–0) ) .log ( 1–0.4)) = 0.222
• コスト関数の結果は次のようになります:

(0.155 + 0.155 + 0.097 + 0.301 + 0.222 + 0.222) / 6 = 0.192

Python コードは次のとおりです:

def BCE (y, y_predicted):
 ce_loss = y*(np.log(y_predicted))+(1-y)*(np.log(1-y_predicted))
 total_ce = np.sum(ce_loss)
 bce = - total_ce/y.size
 return bce

8、ヒンジ損失と二乗ヒンジ損失 (HL および SHL)

ヒンジ損失は、ヒンジ損失またはヒンジ損失と訳されます。ここでは英語が優先されます。

Hinge Loss主要用于支持向量机模型的评估。错误的预测和不太自信的正确预测都会受到惩罚。所以一般损失函数是：

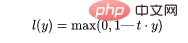
这里的t是真实结果用[1]或[-1]表示。

使用Hinge Loss的类应该是[1]或-1。为了在Hinge loss函数中不被惩罚，一个观测不仅需要正确分类而且到超平面的距离应该大于margin(一个自信的正确预测)。如果我们想进一步惩罚更高的误差，我们可以用与MSE类似的方法平方Hinge损失,也就是Squared Hinge Loss。

如果你对SVM比较熟悉，应该还记得在SVM中，超平面的边缘（margin）越高，则某一预测就越有信心。如果这块不熟悉，则看看这个可视化的例子:

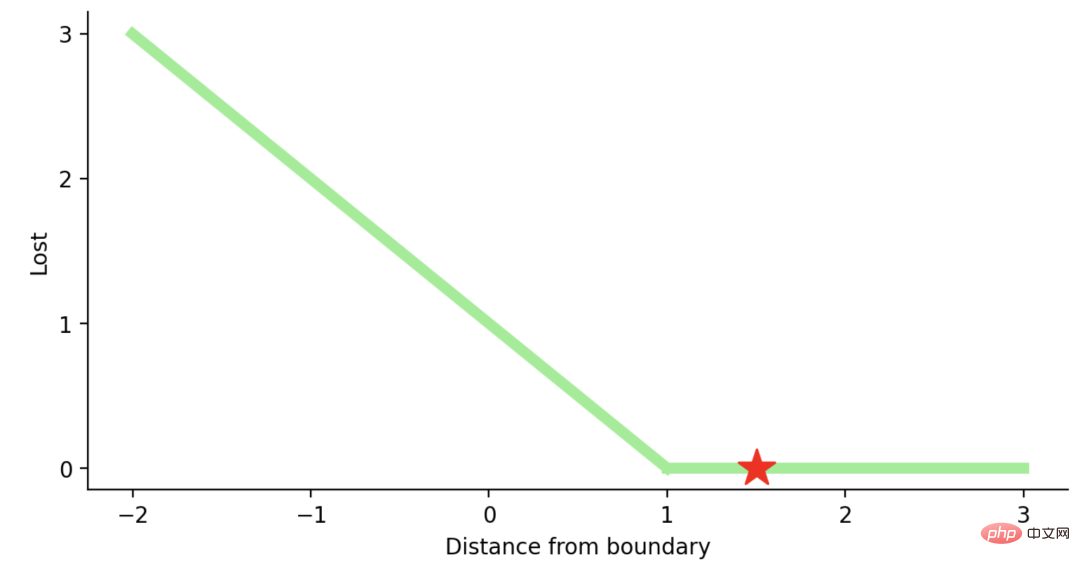
如果一个预测的结果是1.5，并且真正的类是[1]，损失将是0(零)，因为模型是高度自信的。

loss= Max (0,1 - 1* 1.5) = Max (0， -0.5) = 0

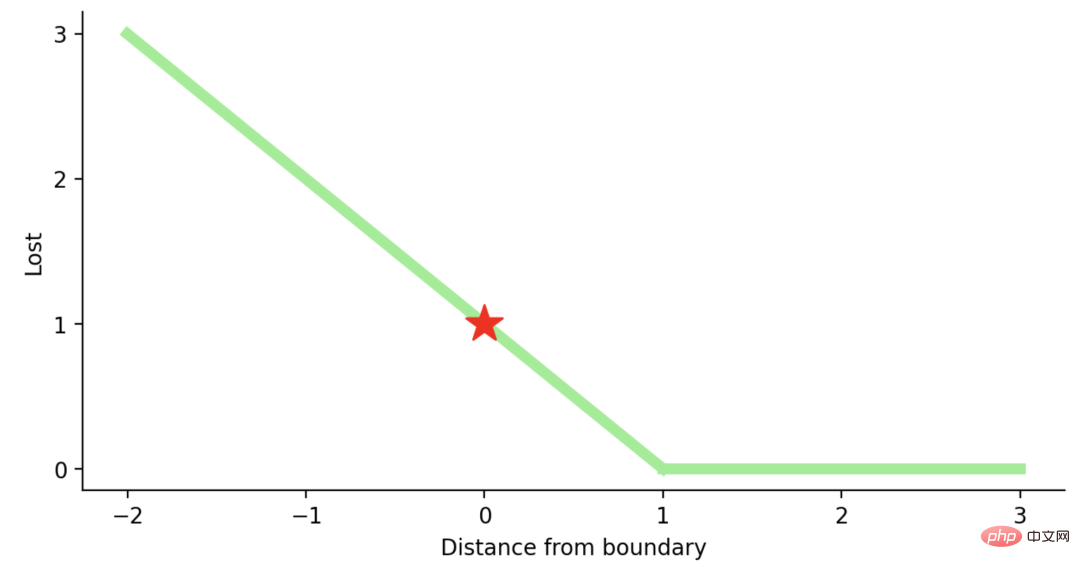
如果一个观测结果为0(0)，则表示该观测处于边界(超平面)，真实的类为[-1]。损失为1，模型既不正确也不错误，可信度很低。

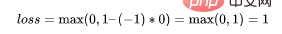
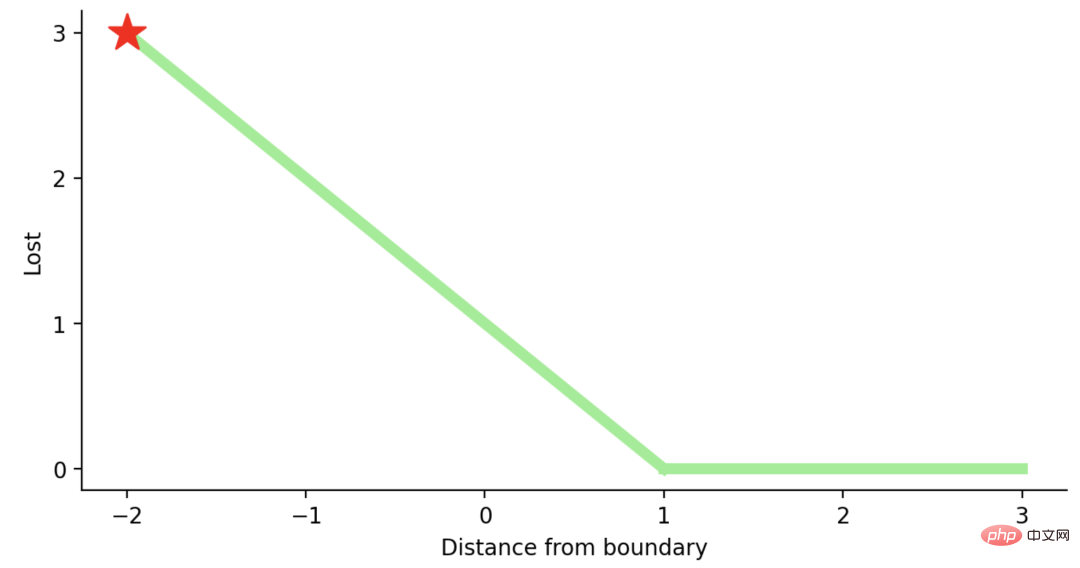
如果一次观测结果为2，但分类错误(乘以[-1])，则距离为-2。损失是3(非常高)，因为我们的模型对错误的决策非常有信心（这个是绝不能容忍的）。

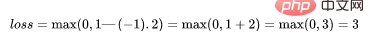
python代码如下：

#Hinge Loss 
def Hinge (y, y_predicted): 
 hinge_loss = np.sum(max(0 , 1 - (y_predicted * y))) 
 return hinge_loss 

#Squared Hinge Loss 
def SqHinge (y, y_predicted): 
 sq_hinge_loss = max (0 , 1 - (y_predicted * y)) ** 2 
 total_sq_hinge_loss = np.sum(sq_hinge_loss) 
 return total_sq_hinge_loss

多分类

9、交叉熵（CE）

在多分类中，我们使用与二元交叉熵类似的公式，但有一个额外的步骤。首先需要计算每一对[y, y_predicted]的损失，一般公式为：

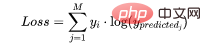
如果我们有三个类，其中单个[y, y_predicted]对的输出是：

这里实际的类3（也就是值=1的部分），我们的模型对真正的类是3的信任度是0.7。计算这损失如下：

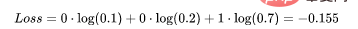
为了得到代价函数的值，我们需要计算所有单个配对的损失，然后将它们相加最后乘以[-1/样本数量]。代价函数由下式给出：

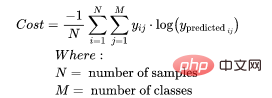
使用上面的例子，如果我们的第二对：

那么成本函数计算如下：

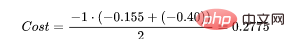
使用Python的代码示例可以更容易理解；

def CCE (y, y_predicted): 
 cce_class = y * (np.log(y_predicted)) 
 sum_totalpair_cce = np.sum(cce_class) 
 cce = - sum_totalpair_cce / y.size 
 return cce

10、Kullback-Leibler 散度 (KLD)

又被简化称为KL散度，它类似于分类交叉熵，但考虑了观测值发生的概率。如果我们的类不平衡，它特别有用。

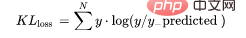
def KL (y, y_predicted): 
 kl = y * (np.log(y / y_predicted)) 
 total_kl = np.sum(kl) 
 return total_kl

以上就是常见的10个损失函数，希望对你有所帮助。

以上がよく使用される損失関数と Python の実装例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。