ホームページ >バックエンド開発 >Python チュートリアル >Python でマジック関数と量子コンピューティング シミュレーションを実装する方法は何ですか?
Python でマジック関数と量子コンピューティング シミュレーションを実装する方法は何ですか?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-04-26 13:22:151785ブラウズ
量子コンピューティング シミュレーションの背景
ProjectQ は、非常にエレガントなオープンソースの量子コンピューティング プログラミング フレームワークであり、そのオリジナルの作成者はスイス連邦研究所のダミアン博士です。テクノロジーとトーマス。この量子コンピューティング プログラミング フレームワークは、量子コンピューティング アプリケーション -> 量子回路コンパイル -> ハミルトニアン シミュレーション -> 量子コンピューティング シミュレーション -> 量子ハードウェア API ドッキング から実装される、非常に包括的な量子コンピューティング プログラミング フレームワークです。 pip を使用したインストールをサポートします: python3 -m pip install projectq --upgrade。
projectq を使用して量子コンピューティングをシミュレートする方法の例を見てみましょう:
[dechin@dechin-manjaro simulator]$ ipython Python 3.8.5 (default, Sep 4 2020, 07:30:14) Type 'copyright', 'credits' or 'license' for more information IPython 7.19.0 -- An enhanced Interactive Python. Type '?' for help. In [1]: from projectq import MainEngine In [2]: from projectq.ops import X In [3]: eng = MainEngine() In [4]: qubits = eng.allocate_qureg(2) In [5]: X | qubits[0] In [6]: from projectq.ops import CX In [7]: CX | (qubits[0], qubits[1]) In [8]: eng.flush() In [9]: print (eng.backend.cheat()[1]) [0j, 0j, 0j, (1+0j)]
この場合、合計 2 量子ビットと、これら 2 ビットの初期状態を割り当てました。これらはすべて |0〉 状態にあり、projectq の出力に対応する振幅ベクトルは [1, 0, 0, 0] になるはずです。このベクトルの 4 つの要素は、それぞれ 4 つの量子状態 00、01、10、および 11 の確率振幅に対応します。特定の状態が測定される確率を計算する必要がある場合は、それに対してモジュロ二乗演算を実行する必要があります。 . :
P(00)=(a00 b00i)(a00−b00i)
確率振幅は複素数 (複素数) であるため、エルミート共役を取得してからドット乗算演算を実行する必要があることに注意してください。
それでは、前述の projectq の使用例に戻りますが、この場合、2 ビットを割り当てた後、最初のビットに対してパウリ行列演算が実行され、CX を演算するためのエンタングルメント ゲートが得られます。ここで、CX(i,j) 量子ゲート演算に対応する演算は次のとおりです: 量子ビット i が |0〉 状態にある場合、演算は実行されません; しかし、量子ビット i が |1〉 状態にある場合、量子ビット j は逆の演算、つまり元の j が |0〉 であれば |1〉 になり、元の j が |1〉 であれば |0〉 になります。これが量子コンピューティングにおける量子もつれの役割であり、実際のハードウェア システムでマルチビット ゲート演算を高品質に実装することは依然として大きな問題です。量子重ね合わせの特性は、量子ビットが |0〉 状態にあることも、|1〉 状態にあることも、あるいは |0〉 と |1〉 の間の中間状態にあることにも反映されます。 |0〉 と |1〉 を確率振幅の形で除算するには: P(0)=(a
0b0i) ⋅(a0−b0i)P(1)=(a
1b1i)&sdot ;(a1−b1i)これらの確率の振幅は、ベクトルの形式で整理できます。
|ε〉 =(a
0b0i,a1 b1i)T最後の要素このベクトルの数は、ビット数が増加するにつれて指数関数的に増加します。ビット数が 41 に増加すると、必要なストレージ メモリ容量は 32TB 以上必要になります。計算プロセス中にすべての確率振幅をメモリにロードする必要があるため、これはハードディスクのストレージ容量とは異なり、メモリだけで 32TB のサイズが必要になることに注意してください。したがって、古典的なコンピューターを使用して量子コンピューティングをシミュレートすることは、実際には非常にリソースを消費する方法です。もちろん、量子コンピューティングシミュレータにはまだ研究価値があり、量子チップの規模や品質を向上させることができない現段階では、シミュレータが重要な役割を果たしています。
Python のマジック関数の実装
読者が Python のマジック関数の詳細かつ包括的な実装について知りたい場合は、この記事の参考リンクから 2 つの優れた記事を入手できます。ここでは、上記の projectq コードの使用例で使用される関数の一部 (__or__ と __str__) にのみ焦点を当て、それらの簡単な再現を作成します。
Python のマジック関数を使用すると、クラスの加算、減算、乗算、除算など、クラスの特別な演算子を定義できます。マジック関数の導入後は、要素を操作する必要はありませんクラス内で個別に作成し、操作をマジック関数でカプセル化できます。最終的な効果は、コード内で演算子を直接使用してさまざまなクラスを操作できることです。たとえば、class1 class2 などの二項演算子をカスタマイズできます。この章では詳しくは紹介しませんが、以下の具体的な使用例やリンク先のブログ投稿を参照してください。
量子状態の定義と実装
最初の章の量子状態ベクトルの導入によると、ここでは単純な量子状態クラスを実装でき、考慮できる量子ビットは 2 つだけです。単純なシステム:
# QubitPair.py
import numpy as np
class QubitPair:
def __init__(self):
self.state = np.array([1, 0, 0, 0], dtype=complex)
def __str__(self):
return str(self.state)この量子状態クラスの定義は非常に単純で、4×1 行列です。ここでは、主にクラスの文字列表現を出力するために使用されるマジック関数 __str__(self) を定義していることを付け加えておきます。たとえば、ここでは量子状態ベクトルを str 形式に直接変換して出力します。次に、カスタム QubitPair クラスを出力すると、現在のクラスに対応する確率振幅の文字列表現が表示されます。
量子ゲート演算の定義と実装
量子ゲート演算については、量子状態ベクトルに作用する行列とみなすことができます。ここでは、まず、定義されたゲート演算の Python を示します。クラスを展開して説明します:
# Operator.py
import numpy as np
class QubitOperator:
"""Pauli rotations and entanglement on qubit-pair"""
def __init__(self, operation=None, theta=0, index=0):
self.index = index
self.name = operation
paulix = np.array([[0, 1], [1, 0]], dtype=complex)
pauliy = np.array([[0, -1j], [1j, 0]], dtype=complex)
pauliz = np.array([[1, 0], [0, -1]], dtype=complex)
cnot = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 0, 1],
[0, 0, 1, 0]])
if operation == 'X' or operation == 'Rx':
self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*paulix
elif operation == 'Y' or operation == 'Ry':
self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliy
elif operation == 'Z' or operation == 'Rz':
self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliz
elif operation == 'CX' or operation == 'CNOT':
self.operation = cnot
def __or__(self, qubitpair):
if self.name == 'CX' or self.name == 'CNOT':
qubitpair.state = np.dot(self.operation, qubitpair.state)
return None
elif self.index == 0:
operation = np.kron(self.operation, np.identity(2))
else:
operation = np.kron(np.identity(2), self.operation)
qubitpair.state = np.dot(operation, qubitpair.state)単位行列とパウリ行列の定義这些是基本的泡利矩阵,这三个两能级体系的泡利矩阵具有非常好的物理性质,如都是酉矩阵且存在特殊的对易关系等: 矩阵指数与旋转门操作 矩阵的指数计算一般采用泰勒级数展开的方法来进行定义: 这里如果我们代入上述介绍的泡利矩阵就会得到这样的结果: CX门操作的定义 在上述提到的所有的量子门操作中,CX是唯一的一个两比特量子门操作,也就是同时作用在两个量子比特上面,其矩阵形式的定义如下所示: 使用魔法函数__or__来实现量子门操作运算 我们首先简单谈一下为什么要用__or__这个魔法函数而不是其他的二元运算符来实现,这点跟开源库ProjectQ是同步的,理由是我们在量子力学中的运算,一般写成如下的形式: |ψt〉=U|ψ0〉 将量子态写成狄拉克符号的形式,中文称为"左矢"和"右矢",英文称之为"bra"和"ket"。因此竖线形式的定义,在形式上会更加契合量子力学的思维,当然,就算是换成其他的符号也是无可厚非的。 在定义了量子态的类和量子门操作的类之后,我们可以写如下所示的一个测试脚本来测试程序的执行效果: 这个程序的测试逻辑为:先定义一个两比特的量子系统,然后对第一个比特执行X门操作,使得其从|0〉态变成|1〉态,再对这两个比特执行纠缠门CX操作,观察其态的变化情况。之后再将第一个比特的状态变回|0〉态,再观察作用CX的态的变化情况,执行结果如下所示: [dechin@dechin-manjaro simulator]$ python3 TestQubits.py 这个结果所展示出来的数字也许比较乱,这是因为在运算过程中的计算精度不足所导致的,这里低于1e-06的数字其实我们可以认为就是0。那么我们从这个结果中可以分析总结出量子态的演变历程: |00〉⇒|10〉⇒|11〉⇒|01〉⇒|01〉 注意:上面的这种写法,其实不太合乎程序语言的逻辑,一般从右到左的方向才是从低位到高位的写法。因此,严格来说写法应该是:|00〉⇒|01〉⇒|11〉⇒|10〉⇒|10〉。 这里我们就完成了基于魔法函数的量子计算模拟的过程,感兴趣的读者可以自行尝试更多的玩法,这里就不进行更多的测试了!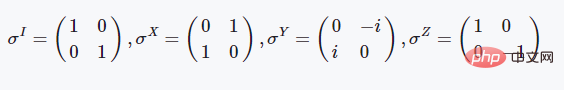
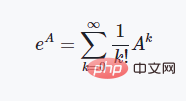
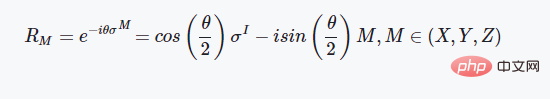

功能测试验证
# TestQubits.py
from QubitPair import QubitPair
from Operator import QubitOperator
if __name__ == '__main__':
qubits = QubitPair()
print ('The initial state is: {}'.format(qubits))
QubitOperator('X', 3.1415926, 0) | qubits
print ('Applying X on the 0th qubit...')
print ('The new state is: {}'.format(qubits))
QubitOperator('CX') | qubits
print ('Applying entanglement on qubits...')
print ('The new state is: {}'.format(qubits))
QubitOperator('X', 3.1415926, 0) | qubits
print ('Applying X on the 0th qubit...')
print ('The new state is: {}'.format(qubits))
QubitOperator('CX') | qubits
print ('Applying entanglement on qubits...')
print ('The new state is: {}'.format(qubits))
The initial state is: [1.+0.j 0.+0.j 0.+0.j 0.+0.j]
Applying X on the 0th qubit...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00-1.j
0.00000000e+00+0.j]
Applying entanglement on qubits...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
0.00000000e+00-1.j]
Applying X on the 0th qubit...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
0.00000000e+00-2.67948966e-08j 0.00000000e+00-2.67948966e-08j]
Applying entanglement on qubits...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
0.00000000e+00-2.67948966e-08j 0.00000000e+00-2.67948966e-08j]
以上がPython でマジック関数と量子コンピューティング シミュレーションを実装する方法は何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

