自動プログラミングNLPモデル技術のレビュー

Copilot、Codex、および AlphaCode: 自己プログラムされたコンピューター プログラムの現状

近年、コード記述の分野でのトランスフォーマーの台頭により、コード記述が驚くほど奥深くなっていることがわかりました。自然言語処理、学習モデル。コンピューター プログラムを作成する能力は、プログラム合成問題と呼ばれることが多く、少なくとも 1960 年代後半から 1970 年代前半にかけて研究されてきました。

2010 年代と 2020 年代、他の分野でのアテンションベースのモデルの成功により、手続き型合成の研究が再び刺激されました。つまり、大規模なシステム向けの数百万または数十の戦略を含む数百ギガバイトのテキストに対する事前トレーニングです。 - 数十億のパラメータを備えたスケール注意ベースのニューラル モデル (トランスフォーマー)。

事前トレーニングされたモデルは、アテンション メカニズムのおかげでメタ学習で優れた機能を実証し、プロンプトを介してテキスト タスクの開発に実際に応用できるようです。ほんの数例 (「ゼロショットまたは少数」と呼ばれます)研究文献の「-ショット学習」）がコンテンツで提供されます。

ディープ NLP モデルに基づく最新の手続き型合成

NLP モデルは、特殊なデータセットを使用してさらにトレーニングし、特定のタスクのパフォーマンスを微調整できます。コードの作成は、このアプリケーションの特に興味深い使用例です。

「あなたの AI ペア プログラマー」として宣伝された GitHub 上の Copilot プロジェクトは、2021 年に開始されたときにかなりの論争を引き起こしました。これは主に、トレーニング データセット内のすべてのパブリック GitHub コードの使用によるものです。指示によると、これらのコード ベースにはコピーレフト ライセンスを持つプロジェクトが含まれており、Copilot 自体がオープン ソースでない限り、Copilot などのプロジェクトでコードを使用することは許可されない可能性があります。

Copilot は、OpenAI 組織と Microsoft Corporation との関係の成果であり、コードトレーニングされたバージョンの GPT-3 に基づいています。 OpenAI によって実証され、その API を通じて利用できるバージョンは Codex と呼ばれます。 Copex を使用した正式な実験の説明は、Chen らが 2021 年に発表した論文で詳しく説明されています。

2022 年初頭、DeepMind も負けじと、独自の手続き的に合成された深層 NLP システムである AlphaCode を開発しました。

新しい挑戦者: AlphaCode

以前の Codex や Copilot と同様、AlphaCode は、コードを書くために設計され、トレーニングされた大規模な NLP モデルです。 Copilot と同様に、AlphaCode は、ソフトウェア エンジニアの生産性ツールとして AlphaCode を使用するために開発されたのではなく、競技プログラミング タスクにおいて人間レベルのプログラミング パフォーマンスに挑戦するために開発されました。

AlphaCode (新しい CodeContests データセットを構成する) のトレーニングと評価に使用されるコンペティション コーディングの課題は、以前のデータセットの難しさと現実世界のソフトウェア エンジニアリングの難しさの間にあります。

競技プログラミング チャレンジ サイトに慣れていない人にとって、このタスクはテスト駆動開発の簡易版に似ています。テキストによる説明といくつかの例を踏まえると、この課題の要点は、一連のテストに合格するプログラムを作成することです (そのほとんどはプログラマーには隠されています)。

理想的には、非表示のテストは包括的である必要があり、すべてのテストに合格することは、特定の問題が正常に解決されたことを意味します。ただし、すべてのエッジケースを単体テストでカバーするのは難しい問題です。プログラム合成の分野への重要な貢献は、実際には CodeContests データセット自体です。DeepMind チームは、偽陽性率 (テストは合格しましたが、問題が発生) を減らすことを目的として、突然変異プロセスを通じて追加のテストを生成するために多大な努力を払ってきました。解決されていない）、陽性率が遅い（テストは合格したが、解決が遅すぎる）。

AlphaCode のパフォーマンスは、コンテスト Web サイト CodeForces の競技プログラミング チャレンジの内容に基づいて評価されます。全体として、競合する (おそらく人間の) プログラマー間の AlphaCode の平均パフォーマンスは「上位 54.3%」でした。

実際には 45.7% のパフォーマンスに相当するため、この指標は少し誤解を招く可能性があることに注意してください。信じられないことに、AlphaCode システムは、すべての隠れたテストに合格するアルゴリズムを作成できます。ただし、注意してください。AlphaCode は、プログラミングの問題を解決するために人間とはまったく異なる戦略を使用します。

人間の競合他社は、以前のバージョンのソリューションを実行して得た洞察を組み込んで、すべてのテストに合格するまで継続的に改善することで、ほとんどのルーチンを解決するアルゴリズムを作成する可能性がありますが、AlphaCode では、より広範なベースのアルゴリズムを採用しています。質問ごとに複数のサンプルを生成し、送信するサンプルを 10 個選択します。

CodeContests データセットでの AlphaCode のパフォーマンスへの大きな貢献は、生成後のフィルタリングとクラスタリングの結果です: 約 1,000,000 個の候補解決策を生成した後、問題の説明に含まれる問題を除去するために候補のフィルタリングを開始します。サンプルテストに不合格となった候補者は、候補者プールの約 99% から除外されます。

著者は、問題の約 10% には、現段階ではすべてのサンプル テストに合格する解決策の候補が存在しないと述べました。

残りの候補は、クラスタリングによって 10 件以下の提出物にフィルタリングされます。つまり、問題の説明に基づいて追加のテスト入力を生成するために別のモデルをトレーニングしました (ただし、これらのテストに対して有効な出力がなかったことに注意してください)。

残りの候補ソリューション (フィルタリング後の数は 1000 未満になる可能性があります) は、生成されたテスト入力の出力に基づいてクラスター化されます。各クラスターから 1 つの候補者が、最大から最小の順に選択されて提出されます。クラスターが 10 個未満の場合、クラスターは複数回サンプリングされます。

フィルタリング/クラスタリングの手順は独特であり、AlphaCode は新しい CodeContests データセットで微調整されていますが、最初は Codex または Copilot とほぼ同じ方法でトレーニングされます。 AlphaCode は、GitHub から大規模に公開されているコード データセット (2021 年 7 月 14 日取得) で最初に事前トレーニングされました。彼らは 5 つのバリアントをトレーニングし、パラメータの数は 2 億 8,400 万から 410 億に増加しました。

AlphaGo シリーズやゲーム StarCraft II をプレイする AlphaStar ロボットと同じ精神で、AlphaCode も、特殊なタスク領域で人間の能力にアプローチするシステムの開発を目的とした研究プロジェクトであり、プロシージャル合成プロセス すぐに使えるユーティリティ プログラムの参入障壁は低くなります。

問題を解決するための実践的なツールの開発という観点から見ると、この分野のロボットの代表的なものは、GPT-3 に準拠した Codex ツールと Copilot ツールです。 Codex は GPT-3 の OpenAI バリアントであり、公開されているコードのコーパスでトレーニングされています。 OpenAI は、論文とともに公開された HumanEval データセットに基づいて、Codex が「docstring to code」形式のタスクで 100 個のサンプルを生成することにより、問題の 70% 以上を解決できると報告しています。

次に、Codex を使用してコードを自動的に生成するプロンプト プログラミング手法を検討します。以下に示すモデルを同時に使用して、ジョン コンウェイのライフ ゲームを開発します。

GitHub Copilot は自動コード補完方式を採用しており、現在のパッケージ化形式は Visual Studio、VSCode、Neovim、JetBrains などの統合開発環境を拡張したものです。 Copilot の Web ページの説明によると、Copilot は、十分にテストされた一連の Python 関数を、指定された説明に従って正常に書き換えることができました。その 57% は HumanEval データ セットに類似しています。

VSCode 用の Copilot 拡張機能の専用ベータ版を使用したテスト作成の自動化など、Copilot の実際の使用例をいくつか見ていきます。

プロンプト プログラミング: Codex を使用した Conway の「Game of Life」の作成

このセクションでは、John Conway の「Game of Life」タスクに基づいたセル オートマトン シミュレーターの作成を紹介します。ルールをハードコーディングせずに、いくつかの変更を加えることで、私たちのプログラムは、本物のようなセル オートマトン ルールのセットをシミュレートできるはずです。

100 個の例を生成し、(手動またはテストの実行によって) 最適な例を選択する代わりに、対話型のアプローチを採用します。 Codex が不適切な解決策を提供した場合、より良い回答を導くために調整を加えます。もちろん、どうしても必要な場合は、Codex が完全に失敗した場合に備えて、コードの変更を続けて動作するサンプルを取得することができます。

現実的な CA (セルラー オートマトン、つまり「セル オートマトン」) を作成します。これは、時間、空間、状態がすべて離散的であり、空間的相互作用と時間的因果関係が局所的であるグリッド ダイナミクス モデルです。複雑なシステムの時空間進化プロセスをシミュレートする機能) シミュレーターの最初のステップは、近傍を計算する関数を提案することです。次の docstring プロンプトを作成し、OpenAI API ライブラリで最大の Codex モデルである code-davinci-001 に提供しました。

# PROMPT<br>import numpy as np<br>def compute_neighborhood(grid: np.array) -> np.array:<br>"""<br>Compute the sum of cell states in the Moore neighborhood<br>for each cell in the input grid.<br>A Moore neighborhood includes 8 cells,<br>diagonally and orthogonally adjacent to, but not including, the center cell.<br>The cells denoted by '1' correspond to the Moore neighborhood for cell a:<br>1 1 1<br>1 a 1<br>1 1 1<br>If cell 'a' is on the edge of the grid,<br>the Moore neighborhood wraps around to the cells on the opposite edge,<br>i.e. grid is on a toroid.<br><br>args:<br>grid, a numpy array with binary values 0 or 1. grid contains the current cell state values<br>Returns:<br><br>neighorhood_grid, a numpy array with integer values from 0 to 8.<br>For each cell (element in grid) in grid, neighborhood_grid should<br>contain the sum of states in that cell's Moore neighborhood<br>"""

上記のコードに、コメント行「# PROMPT」と「」を追加します。 #GENERATED」は、プロンプトがどこで終わるのかを明確にするためのものです。

上記のかなり包括的な docstring プロンプトを注意深く分析しましたか?コーデックスはどのように機能しますか?実際、Codex での最初の試みは次のようになりました:

# GENERATED<br># TODO: implement this function<br>pass

これはおそらく、私たちの小さな実験には良い前兆ではありません。 P 値ハイパーパラメータを調整してより緩やかなカーネル サンプリング (そして願わくばより優れた多様性) を実現した後でも、Codex は上記の質問に対する答えをまだ持っていないようです。

幸いなことに、次のようなものを docstring プロンプトに追加するだけで、Codex はより有望な出力を生成します。

# PROMPT (appended to previous prompt)<br><br>this function is completed and does not include any TODOs<br>"""<br><br># GENERATED<br><br># get the dimensions of the grid<br>n_rows, n_cols = grid.shape<br><br># initialize the output array<br>neighborhood_grid = np.zeros((n_rows, n_cols), dtype=int)<br><br># loop over the grid<br>for i in range(n_rows):<br>for j in range(n_cols):<br><br># get the current cell value<br>cell_val = grid[i, j]<br><br># get the Moore neighborhood of the current cell<br># using the get_neighborhood function<br>neighborhood = get_neighborhood(grid, i, j)<br><br># sum the cell values in the neighborhood<br>neighborhood_sum = np.sum(neighborhood)<br><br># store the sum in the neighborhood grid<br>neighborhood_grid[i, j] = neighborhood_sum<br><br>return neighborhood_grid

もちろん、これはまだあまり良い解決策ではありません。未使用の変数 cell_val が導入され、その作業のほとんどが、追加したばかりの別の関数 get_neighborhood に委譲されます。しかし全体的には、実現可能なスタートのように見える。

次に、上記の get_neighborhood 関数の単純な docstring を作成しました:

def get_neighborhood(grid: np.array, i: int, j: int) -> np.array:<br>"""<br>get_neighborhood is used by compute_neighborhood <br>to return the 3x3 Moore neighborhood for the cell <br>located at coordinates i,j If i,j coordinates are <br>on the edge of the grid (i.e. i or j equal 0, or i == <br>grid.shape[0]-1 or j == grid.shape[1]), the Moore<br>Neighborhood should wrap around to include cells on the<br>opposite edge. In other words the grid can be considered to <br>be the surface of a toroid, like 'Pac-Man'<br><br>args:<br>grid, np.array, this is the current state of<br>the cellular automata grid<br>i, int, this coordinate corresponds to the row<br>j, int, coordinate corresponding to column<br><br>returns:<br>moore_neighborhood - np.array, should always have<br>dimensions 3x3 and<br>contain the Moore neighborhood for the cell at i,j <br>in grid.Because the center cell is not part of the<br>neighborhood, moore_neighborhood[1,1] should always <br>be 0<br>"""<br><br># GENERATED<br><br># get the dimensions of the grid<br>n_rows, n_cols = grid.shape<br><br># initialize the output array<br>moore_neighborhood = np.zeros((3, 3), dtype=int)<br><br># get the coordinates of the Moore neighborhood<br># using the get_neighborhood_coordinates function<br>neighborhood_coords = <br>get_neighborhood_coordinates(i, j, n_rows, n_cols)<br><br># loop over the coordinates<br>for coord in neighborhood_coords:<br># get the cell value at the coordinate<br>cell_val = grid[coord[0], coord[1]]<br><br># store the cell value in the output array<br>moore_neighborhood[coord[0], coord[1]] = cell_val<br><br>return moore_neighborhood

上記のプログラムの出力は実行可能に見えますが、検査した結果、実際には重要な間違いが含まれています。

近傍座標のループでは、グリッドから値を取得するために使用したのと同じ座標を使用して、値をムーア近傍に割り当てます。

Codex にエラーを回避するよう促す明確な方法が見つからなかったので、コードを手動で変更する必要がありました:

# FIXED loop over the coordinates <br>for index, coord in enumerate(neighborhood_coords): <br># get the cell value at the coordinate<br>cell_val = grid[coord[0], coord[1]] <br><br># FIXED store the cell value in the output array<br>moore_neighborhood[index // 3, index % 3] = cell_val<br><br>return moore_neighborhood

さらに、別の関数 get_neighborhood_coowned が前のコードに導入されました。より「トリッキーな」部分を処理します。

次に、関数 get_neighborhood_coodys のプロンプトを作成する必要があります。

# PROMPT <br>def get_neighborhood_coordinates(<br>i: int, j: int, n_rows: int, n_cols: int) -> list:<br>"""<br>get_neighborhood_coordinates is used by get_neighborhood <br>to return the coordinates of the 3x3 Moore neighborhood for<br>the cell located at coordinates i,j If i,j coordinates are on<br>the edge of the grid (i.e. i or j equal 0, or i ==<br>grid.shape[0]-1 or j == grid.shape[1]), the Moore<br>Neighborhood should wrap around to include cells on the<br>opposite edge. In other words the grid can be considered to <br>be the surface of a toroid, like 'Pac-Man'<br><br>args:<br>i, int, this coordinate corresponds to the row<br>j, int, coordinate corresponding to column<br>n_rows, int, number of rows in the grid<br>n_cols, int, number of columns in the grid<br><br>returns:<br>neighborhood_coords - list of tuples, <br>each tuple contains the coordinates<br>of a cell in the Moore neighborhood<br>"""<br><br># GENERATED<br><br># initialize the output list<br>neighborhood_coords = []<br><br># get the coordinates of the Moore neighborhood<br># using the get_neighborhood_coordinates function<br>for row in range(i-1, i+2):<br>for col in range(j-1, j+2):<br># skip the center cell<br>if row == i and col == j:<br>continue<br><br># check if the cell is on the edge of the grid<br># if so, wrap around to the opposite edge<br>if row row = n_rows - 1<br>elif row == n_rows:<br>row = 0<br><br>if col col = n_cols - 1<br>elif col == n_cols:<br>col = 0<br><br># store the cell coordinates<br>neighborhood_coords.append((row, col))<br><br>return neighborhood_coords

这比我们预期的函数式编程深度要深一点（compute_neighborhood调用get_neighborhood，反过来get_neighborhood又调用get_neighborhood_coordinates），但看起来我们终于有了一组函数，可以返回一个邻居和的网格。

还剩下update函数，它对应的docstring提示如下所示：

# PROMPT<br><br>def update_grid(grid: np.array, rules: list) -> np.array:<br>"""<br>update input arg grid according the the Life-like rules<br>contained in input arg rules. rules is a list of lists, <br>with the first element containing a list of 'birth'<br>conditions (cells go from 0 -> 1) and the second element<br>containing a list of 'survival' conditions (cells are<br>unchanged).<br>Cells which have a neighborhood sum that is not in the<br>'birth' (B) or 'survival' (S) rules go to 0. <br><br>This functions uses function compute_neighborhood to compute <br>the neighborhood value for each cell in grid.<br><br>args:<br>grid, np.array. grid contains the cell values (0 or 1)<br> rules, list of lists. rules contains the B/S rules <br> for Life-like cellular automatafor example, to<br> simulate Conway's Life CA, `rules = [[3], [2,3]]`,<br> i.e. B3/S23 Life Without Death has rules<br> B3/S012345678, so `rules = [[3],<br> [0,1,2,3,4,5,6,7,8]]`<br><br>update_grid should raise an Exception if rules contains <br>values greater than 8 (maximum number of live cells in a<br>Moore neighborhood) or less than 0. <br>"""<br><br># GENERATED<br><br># get the dimensions of the grid<br>n_rows, n_cols = grid.shape<br><br># get the neighborhood grid<br>neighborhood_grid = compute_neighborhood(grid)<br><br># loop over the grid<br>for i in range(n_rows):<br>for j in range(n_cols):<br># get the current cell value<br>cell_val = grid[i, j]<br><br># get the neighborhood value for the current cell<br>neighborhood_val = neighborhood_grid[i, j]<br><br># check if the cell is alive<br>if cell_val == 1:<br># check if the cell should die<br>if neighborhood_val not in rules[1]:<br>grid[i, j] = 0<br>else:<br># check if the cell should be born<br>if neighborhood_val in rules[0]:<br>grid[i, j] = 1<br><br>return grid

这看起来是解决上面问题的一种非常合理的方法；尽管我们确实明确建议，如果邻居网格包含错误的值并且在生成的输出中找不到，就会引发异常。

只需进行一些修复：在函数get_neighborhood中进行手动干预，并且尝试给出一些提示，我们就可以成功地设计出一个完全可行的类似生命的细胞自动机模拟器。

上面的代码不是一个特别快的实现方案，但它的质量与程序员在开始使用一种新语言时可能做出的那种“Hello World”尝试相似。值得注意的是，在训练数据集中包含了许多示例，供研究者参考。

在康威的《生命游戏》中，我们可以想象这段程序在微型滑翔机的发展过程中取得的成功。

虽然我们确实通过一组函数完成了CA模拟器的编写，但这种方法对于日常软件工程来说并不是非常有用或现实的开发方式。但另一方面，这并不能阻止像SourceAI这样的初创公司（本质上是OpenAI Codex API的包装商）将其服务宣传为“给每个人创造有价值的定制软件的机会”。

“我们构建了一个独立的系统，可以开发出世界上最熟练的工程师级别的软件。”不过，与Codex交互的确是学习或实践编程的一种潜在有用的方式，尤其是针对CodeSignal、CodeForces或HackerRank等网站的编程问题方面。

接下来，我们将尝试评估Codex/Copilot，以获得自动编写测试和docstring的更现实的使用情形。

任务2：编写测试

对于本例来说，我们选择使用VSCode开发工具的GitHub Copilot扩展来编写测试。

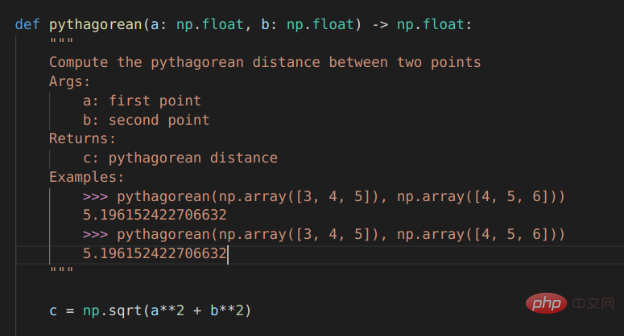
# PROMPT (in VSCode)<br>import numpy as np<br>def pythagorean(a: np.float, b: np.float) -> np.float:<br>"""<br>Use the Pythagorean theorem to comput the hypotenuse for<br>a triangle with side lengths a and b<br><br>args:<br>a, np.float, side of the triangle<br>b, np.float, the other side of the triangle<br><br>returns:<br>c, np.float, the length of the hypotenuse<br>"""<br>c = np.sqrt(a**2 + b**2)<br>return c<br><br>def test_pythagorean():<br><br># GENERATED (Copilot autocomplete)<br>"""<br>Test the pythagorean function<br>"""<br>a = np.array([3, 4, 5])<br>b = np.array([4, 5, 6])<br>c = pythagorean(a, b)<br><br>assert np.allclose(c, np.sqrt(a**2 + b**2))

虽然毕达哥拉斯定理函数可能过于简单，但Copilot建议进行一次合理的测试。如果您运行它，它就会通过。你会注意到，自动完成建议能够正确地获得测试的结构和数字内容。

如果我们想使用自己喜欢的框架以更系统的方式编写测试，该怎么办？不用太担心，因为我们已经使用numpy库和自动微分技术编写了大量的低级学习模型，供给测试者使用。因此，虽然接下来的这个示例不是100%真实地来自真实世界，但效果还是比较贴近真实情况的。

在本例中，我们将使用autograd和numpy以及unittest中的TestCase类设置一个简单的多层感知器前向传递、损失函数和梯度函数进行测试。

#PROMPT<br>import unittest<br>from autograd import numpy as np<br>from autograd import grad<br><br>def forward_mlp(input_x: np.array, <br>weights: list, biases: list) -> np.array:<br>"""<br>compute the forward pass of a multilayer perceptron. <br>The number of layers is equal to the length of the list of<br>weights, which must be the same as the list of biases,<br>biases. <br><br>args:<br>input_x, np.array, input data<br>weights, list of np.arrays, a list of np.array matrices,<br> representing the weights<br>biases: list of np.arrays, a list of biases for each<br> layer<br><br>returns:<br>result, np.array, the output of the network<br>"""<br><br>assert len(weights) == len(biases)<br><br>for layer_index in range(len(weights) - 1):<br>input_x = np.tanh(np.matmul(input_x,<br>weights[layer_index]) + biases[layer_index])<br><br>output = np.matmul(input_x, weights[-1]) + biases[-1]<br>return output<br>def get_loss(input_x: np.array, weights: list, <br>biases: list, target: np.array) -> np.float:<br>"""<br>compute the mean squared error loss for an mlp with weights<br>and biases, with respect to the input data input_x and the<br>target array target.<br><br>args:<br>input_x, np.array, input data<br>weights, list of np.arrays, a list of np.array matrices,<br>representing the weights<br>biases: list of np.arrays, a list of biases for each<br>layer<br>target: np.array, the target values<br><br>returns:<br>loss, np.float, the loss<br>"""<br><br>output = forward_mlp(input_x, weights, biases)<br><br>return np.mean((output - target)**2)<br><br>get_loss_grad = grad(get_loss, argnum=(1,2))<br><br><br>class TestMLP(unittest.TestCase):<br>"""<br>tests for MLP, get_loss, and get_grad_loss<br>"""<br># GENERATED (chosen from Copilot suggestions)<br>def setUp(self):<br>pass<br><br>def test_forward_mlp(self):<br>"""<br>test forward_mlp<br>"""<br><br>input_x = np.array([[1, 2, 3], [4, 5, 6]])<br>weights = [np.array([[1, 2], [3, 4]]), <br>np.array([[5, 6], [7, 8]]), <br>np.array([[9, 10], [11, 12]])]<br>biases = [np.array([[1, 2]]), np.array([[3, 4]]),<br>np.array([[5, 6]])]<br><br>output = forward_mlp(input_x, weights, biases)<br>self.assertTrue(np.allclose(output, <br>np.array([[-0.9, -0.9], [-0.9, -0.9]])))<br><br>def test_get_loss(self):<br>"""<br>test get_loss<br>"""<br>input_x = np.array([[1, 2, 3], [4, 5, 6]])<br>weights = [np.array([[1, 2], [3, 4]]), <br>np.array([[5, 6], [7, 8]]), <br>np.array([[9, 10], [11, 12]])]<br>biases = [np.array([[1, 2]]), np.array([[3, 4]]),<br>np.array([[5, 6]])]<br>target = np.array([[1, 1], [1, 1]])<br><br>loss = get_loss(input_x, weights, biases, target)<br><br>self.assertTrue(np.allclose(loss, 0.5))<br><br>def test_get_loss_grad(self):<br>"""<br>test get_loss_grad<br>"""<br><br>input_x = np.array([[1, 2, 3], [4, 5, 6]])<br>weights = [np.array([[1, 2], [3, 4]]), <br>np.array([[5, 6], [7, 8]]), <br>np.array([[9, 10], [11, 12]])]<br>biases = [np.array([[1, 2]]), np.array([[3, 4]]),  <br>np.array([[5, 6]])]<br>target = np.array([[1, 1], [1, 1]])<br><br>loss_grad = get_loss_grad(<br>input_x, weights, biases, target)<br><br>self.assertTrue(<br>np.allclose(loss_grad[0], <br>np.array([[-0.9, -0.9], [-0.9, -0.9]])))<br>self.assertTrue(<br>np.allclose(loss_grad[1], <br>np.array([[-0.9, -0.9], [-0.9, -0.9]])))<br>self.assertTrue(<br>np.allclose(loss_grad[2],<br>np.array([[-0.9, -0.9], [-0.9, -0.9]])))<br><br># END GENERATED (the final two lines are part of the prompt)<br>if __name__ == "__main__":<br>unittest.main(verbosity=1)

Copilot的建议虽然并不完美，但确实为测试类提供了合理的思路。不过，如果您尝试原封不动地运行代码的话，则不会执行任何测试，更不用说通过测试了。

输入数据和第一个权重矩阵之间存在维度不匹配，数据类型也是错误的（所有数组都是整数数据类型），而且无法使用Autograd梯度函数。

当然，上面这些问题并不是很难解决，如果用3x2矩阵替换权重矩阵列表中的第一个条目，那么前向传播应该可以运行。要使得梯度计算测试顺利进行，或者需要在np.array定义的数字上添加小数点，或者显式定义数组数据类型。

有了这些更改后，测试即可成功执行并失败，但预期值在数字表现方面还不正确。

任务3：自动文档字符串

Copilot有很大潜力的一项任务是自动编写文档，特别是为已经编写的函数填写docstring内容。这方面几乎是比较实用了。

对于毕达哥拉斯定理的示例程序，Copilot运行结果已经非常接近，但它将问题描述为查找两点a和b之间的距离，而不是查找边长c到边长a和边长b的距离。不出所料，随同Copilot一同发行的docstring中的示例也与函数的实际内容不匹配：返回的是一个标量，而不是c的值数组。

Copilot对前向MLP函数的docstrings的建议也很接近，但并不完全正确。

Copilot支持的自动Docstring建议

机器能取代我的工作吗？

对于软件工程师来说，程序合成方面的每一项新进展都可能引发一次经济恐慌。

結局のところ、コンピュータープログラムがプログラマーと同じようにコンピューターをプログラムできるのであれば、機械が「私たちの仕事を奪う」べきということにはならないでしょうか?近い将来、そうなるのでしょうか？

表面的には、答えは「まだ」であるように見えますが、これらのツールがより成熟しても、ソフトウェア エンジニアリングの性質が変わらない可能性が高いという意味ではありません。将来的には、推論を成功させるために高度なオートコンプリート ツールを使用することが、コード フォーマット ツールを使用するのと同じくらい重要になる可能性があります。

Copilot は現在ベータ版であり、使用方法のオプションの数が限られています。同様に、Codex にも OpenAI を通じてベータ版で利用できる API があります。パイロット プログラムの利用規約とプライバシーに関する考慮事項により、このテクノロジーの潜在的な使用例が制限されます。

現在のプライバシー ポリシーに従って、これらのシステムに入力されたコードはモデルの微調整に使用でき、GitHub/Microsoft または OpenAI スタッフがレビューできます。これにより、機密性の高いプロジェクトで Codex または Copilot を使用する可能性が排除されます。

Copilot は、ベースとなる Codex モデルに多くのユーティリティを追加します。必要なコードのスケルトンまたはアウトラインを作成し (単体テスト フレームワークのテストの例を作成するなど)、アウトラインの中央にカーソルを移動すると、賢明な OK オートコンプリートの提案が表示されます。

現時点では、Copilot は、単純なコーディングの実践よりも複雑な問題に対して、正しい完全なコードを提案することはほとんどありませんが、通常は合理的なアウトラインを作成し、手作業での入力を省略できます。

Copilot はクラウドで実行されることにも注意してください。これは、オフラインでは機能せず、オートコンプリートの提案が少し遅いことを意味します。この時点で、Alt ] キーの組み合わせを押すと、候補を切り替えることができますが、選択できる候補が 2 ～ 3 個しかない場合や、選択できる候補が 1 つしかない場合があります。

Copilot がうまく機能する場合、それは実際には少し危険であるのに十分です。単体テストの例で提案されているテストと、ピタゴラス関数について提案されている docstring は、一見すると正しいように見え、おそらく、うんざりしたソフトウェア エンジニアの精査を通過するでしょう。しかし、それらに不可解なエラーが含まれている場合、これは後で問題を引き起こすだけです。

要約すると、Copilot/Codex は、現状ではおもちゃか学習ツールに近いものですが、実際に動作するのは驚くべきことです。ワルツを踊るクマに出会ったら、その踊りの上手さでは感銘を受けることはないと思います。同様に、スマートなコード補完ツールに出会った場合、感動するのは、そのツールが作成するコードの完璧さであってはなりません。

つまり、自動プログラミング NLP モデル テクノロジがさらに発展し、NLP 自動補完ツールを使用するために人間のプログラマーによって行われる多数の調整により、プログラムの主要なキラー アプリケーションが登場する可能性があります。近い将来の合成モデル。

翻訳者紹介

Zhu Xianzhong 氏、51CTO コミュニティ編集者、51CTO エキスパートブロガー、講師、濰坊市の大学のコンピューター教師、フリーランスプログラミング業界のベテラン。初期の頃は、さまざまな Microsoft テクノロジに焦点を当てていました (ASP.NET AJX および Cocos 2d-X に関連する 3 冊の技術書籍を編集しました)。過去 10 年間は、オープンソースの世界に専念してきました (人気のある完全なソースに精通しています)。スタックWeb開発技術）を学び、OneNet/AliOS Arduino/ESP32/Raspberry PiなどのIoT開発技術やScala Hadoop Spark Flinkなどのビッグデータ開発技術について学びました。

元のタイトル: コードを書くための NLP モデル: プログラム合成、著者: ケビン・ヴー

###

以上が自動プログラミングNLPモデル技術のレビューの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。