ホームページ >テクノロジー周辺機器 >AI >スパースモデルの最新の進歩! Ma Yi 氏と LeCun 氏が協力: 「ホワイト ボックス」教師なし学習
スパースモデルの最新の進歩! Ma Yi 氏と LeCun 氏が協力: 「ホワイト ボックス」教師なし学習
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-04-12 08:34:02971ブラウズ
最近、Ma Yi 教授とチューリング賞受賞者の Yann LeCun が共同で ICLR 2023 で論文を発表しました。この論文では、データ拡張、ハイパーパラメータ調整、その他のエンジニアリング設計に頼る必要のない、最小限で解釈可能な教師なし学習方法について説明しています。 SOTA SSL 方式に近いパフォーマンスを実現します。

#紙のリンク: https://arxiv.org/abs/2209.15261
#この方法では、スパース多様体変換を利用し、スパース コーディング、多様体学習、低速特徴分析を組み合わせます。単層の決定論的スパース多様体変換を使用すると、MNIST で 99.3% の KNN トップ 1 精度、CIFAR-10 精度で 81.1% の KNN トップ 1 精度を達成できます。 CIFAR-100 では KNN トップ 1 の精度が 53.2% に達します。
単純なグレースケール強化により、CIFAR-10 と CIFAR-100 のモデルの精度はそれぞれ 83.2% と 57% に達しました。これらの結果により、単純な「ホワイト ボックス」手法と SOTA が大幅に削減されました。方法。
さらに、この記事では、教師なし表現変換を形成する方法について視覚的に説明します。この方法は、潜在埋め込み自己教師あり方法と密接に関連しており、最も単純な VICReg 方法とみなすことができます。

この記事の筆頭著者である Yubei Chen は、ニューヨーク大学のデータ サイエンス センター (CDS) およびメタ基礎人工知能研究 (FAIR) の博士研究員助手です。指導教員はヤン・ルカン教授で、カリフォルニア大学バークレー校のカリフォルニア理論神経科学レッドウッドセンターとバークレー人工知能研究所(BAIR)で博士号を取得し、清華大学で学士号を取得しました。

Ma Yi 教授は、1995 年に清華大学でオートメーションと応用数学の二重学士号を取得し、1997 年にカリフォルニア大学バークレー校で EECS の修士号を取得し、修士号を取得しました。 2000年に数学とEECSで博士号を取得。彼は現在、カリフォルニア大学バークレー校の電気工学およびコンピュータサイエンス学部の教授であり、IEEE フェロー、ACM フェロー、および SIAM フェローでもあります。
Yann LeCun は、光学式文字認識とコンピューター ビジョンで畳み込みニューラル ネットワーク (CNN) を使用した研究で最もよく知られています。彼は畳み込みネットワークの父としても知られており、2019 年には畳み込みネットワークの父としても知られています。 Bengio 氏とヒントン氏は共同で、コンピューター サイエンスの最高賞であるチューリング賞を受賞しました。
最も単純な教師なし学習から始める
過去数年で、教師なし表現学習は大きな進歩を遂げ、データ駆動型マシンでの使用が期待されています。学習における強力なスケーラビリティ。
しかし、学習された表現とは何か、それが教師なしの方法で正確にどのように形成されるのかはまだ不明であり、さらに、これらすべての教師なしの共通原則をサポートするツールのセットがあるかどうかも不明です。表現は依然として不明瞭である。
多くの研究者は、モデルの理解を向上させることの重要性を認識し、SOTA 手法を簡素化し、古典的な手法との接続を確立し、表現を視覚化するためのさまざまな手法を統合するために、いくつかの先駆的な措置を講じてきました。そして、これらの手法を理論的観点から分析し、別の計算理論を開発することを目指しています。第一原理モデルに基づいてデータからシンプルで完全に解釈可能な「ホワイト ボックス」を構築できる理論であり、この理論は理解のための指針も提供できます。人間の脳における教師なし学習の原理。
今回の研究では、研究者らはこの目標に向けてさらに小さな一歩を踏み出し、ディープネットワーク、プロジェクションヘッド、データ拡張、またはその他のさまざまな工学設計を必要としない、最も単純な「ホワイトボックス」教師なし学習モデルの構築を試みました。
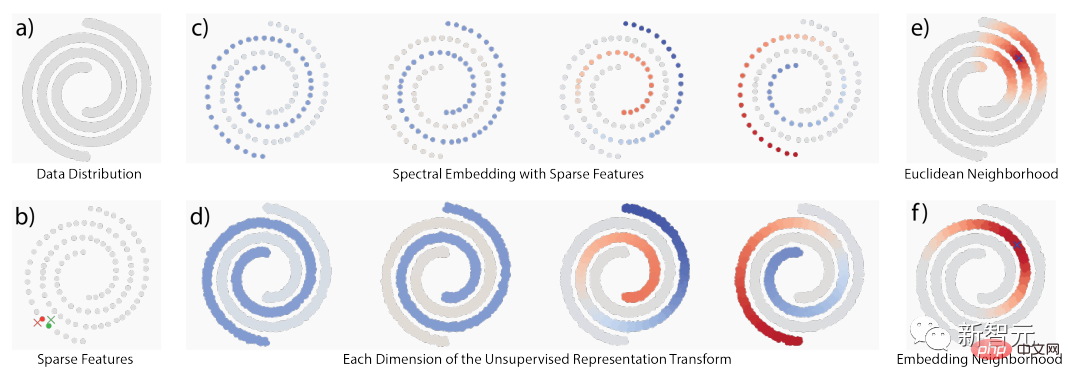
この記事では、スパース性とスペクトル埋め込みという 2 つの古典的な教師なし学習原理、つまり 2 層モデルを使用します。が構築され、いくつかの標準データセットで有意ではないベンチマーク結果が得られました。
実験結果は、スパース多様体変換に基づく 2 層モデルが潜在埋め込み自己教師あり手法と同じ目的を持っており、データを拡張しなくてもパフォーマンスが向上することを示しています。この場合、MNIST では KNN の最高レベル 1 精度の 99.3%、CIFAR-10 では KNN の最高レベル 1 精度の 81.1%、CIFAR-100 では 53.2% の精度を達成しました。
シンプルなグレースケール強化により、CIFAR-10 では 83.2% の KNN トップ 1 精度、CIFAR-100 では 57% の KNN トップ 1 精度をさらに達成しました。
これらの結果は、「ホワイト ボックス」モデルと SOTA 自己教師あり (SSL) モデルの間のギャップを埋めるための重要な一歩を踏み出しました。ギャップを埋めることで、教師なし表現の学習をより深く理解することが可能になり、これはこの理論の実用化に向けた有望な研究ラインでもあります。
#3 つの基本的な質問教師なし (自己教師あり) 再プレゼンテーションとは何ですか
##本質的に、元の信号の非同一変換はすべて表現 (再プレゼンテーション) と呼ぶことができますが、学術コミュニティはそれらの有用な Convert に関心を持っています。
教師なし再プレゼンテーション学習のマクロ目標は、元のデータを新しい空間に変換して、「類似した」ものが互いに近くに配置されるようにする関数を見つけることです。 、新しい空間は折りたたまれて自明であってはなりません。つまり、データの幾何学的またはランダムな構造が保存されなければなりません。
この目標が達成された場合、「異なる」コンテンツは自然に表現空間の遠くに配置されることになります。
類似性はどこから来るのでしょうか?
類似性は主に、1) 時間的共起、2) 空間的共起、3) 元の信号空間における局所的隣接という 3 つの古典的な考え方に基づいています。 )。
基礎となる構造が幾何学的構造である場合、これらの考え方はかなりの部分で重複しますが、構造がランダムな構造である場合、以下に示すように概念的にも異なります。多様体構造と確率的共起構造の間。
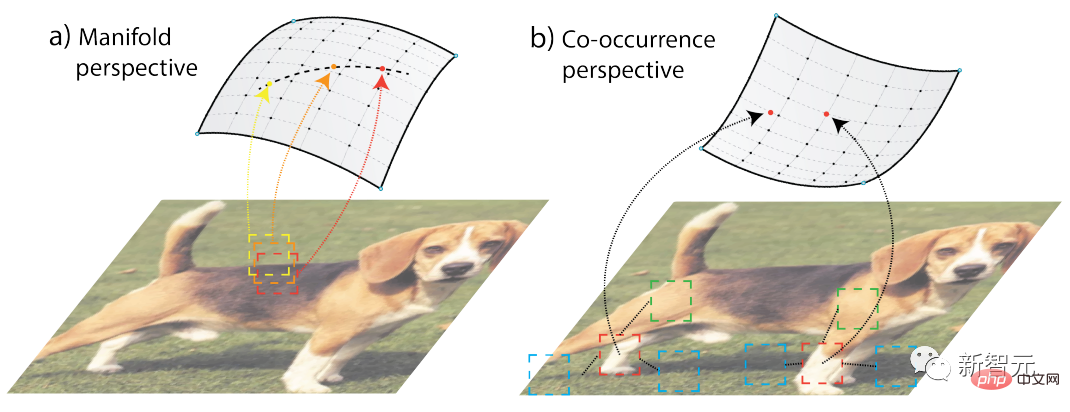
関連研究では、局所性を利用して、2 つの教師なし学習方法を提案しています: 多様体学習と共起統計モデリング、多くのこれらのアイデアのうち、リネージ分解の定式化、または密接に関連する行列分解の定式化に到達するものもあります。
多様学習の考え方は、元の信号空間のローカル近傍のみが信頼できるというものであり、すべてのローカル近傍を包括的に考慮することで、グローバルな幾何学が現れます。 、ローカルにフィットする」(グローバルに考え、ローカルにフィットする)。
対照的に、共起統計モデリングは確率論的な哲学に従います。一部の構造は連続多様体ではモデル化できないため、多様体の哲学を補完するものでもあります。
最も明白な例の 1 つは自然言語からのものです。自然言語では、元のデータは基本的に、単語の埋め込みや「シアトル」や「ダラスの埋め込み」などの滑らかなジオメトリから取得されません。 」は、頻繁に共起しない場合でも似ている可能性がありますが、根本的な理由は、それらが類似した文脈パターンを持っていることです。
確率と多様体の視点は、「類似性」を理解する上で互いに補完的です。類似性の定義があれば、類似した概念を近づけるための変換を構築できます。
#この記事では表現変換を確立する方法を教えてください。基本原則: スパース性と低ランク
一般に、スパース性を使用してデータ空間内の局所性と分解を処理し、サポートを確立できます。その後、低頻度関数が使用されます。サポート上の同様の点に同様の値を割り当てる表現変換を構築します。
このプロセス全体をスパース多様体変換 (スパース多様体変換) と呼ぶこともできます。
以上がスパースモデルの最新の進歩! Ma Yi 氏と LeCun 氏が協力: 「ホワイト ボックス」教師なし学習の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

