信じられない！ Numpy を使用して深層学習フレームワークを開発し、ニューラル ネットワークのトレーニング プロセスを調査する

＃＃＃こんにちは、みんな。

今日は、非常に素晴らしいオープン ソース プロジェクトを共有したいと思います。深層学習フレームワークは Numpy を使用して開発されました。構文は基本的に Pytorch と同じです。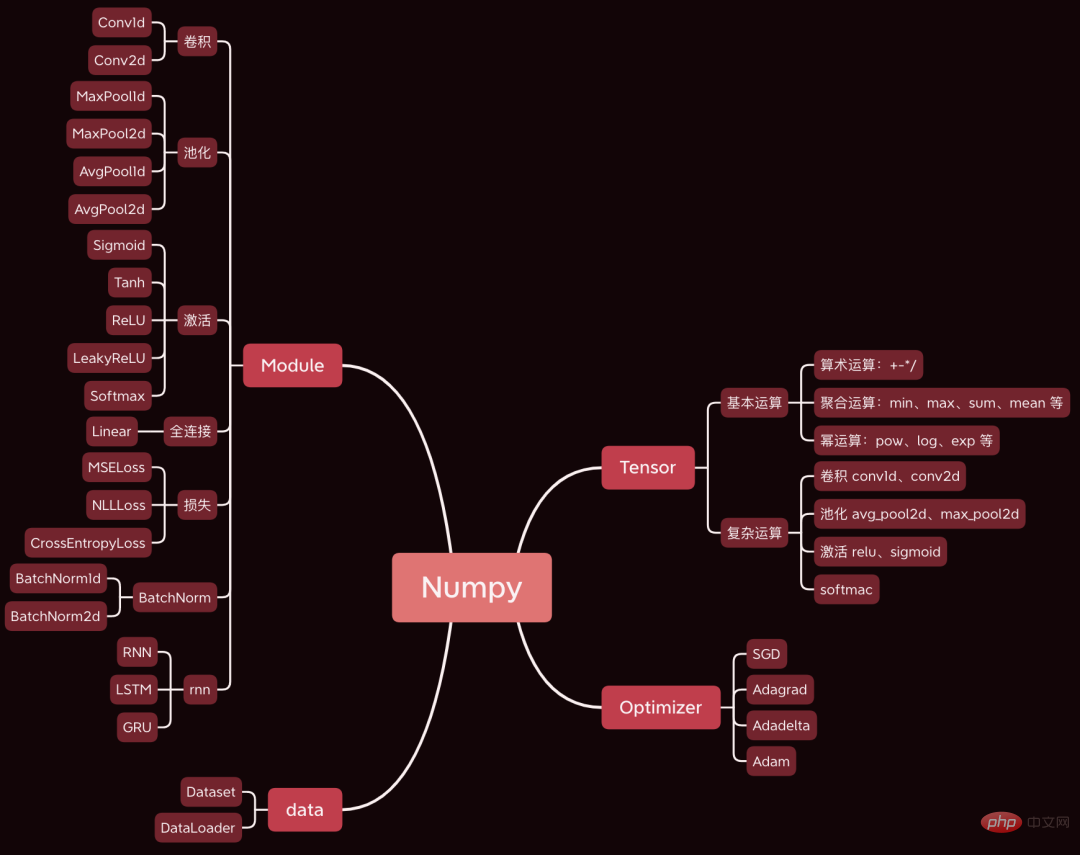

今日は、単純な畳み込みニューラル ネットワークを例として、順伝播、逆伝播、パラメーターの最適化など、ニューラル ネットワークのトレーニング プロセスに含まれる中心的なステップを分析します。 。 ソースコード。

使用したデータセットとコードはパッケージ化されており、それらを入手する方法は記事の最後にあります。

1.準備

まずデータとコードを準備します。

1.1 ネットワークを構築する

まず、フレームワークのソース コードをダウンロードします。アドレス: https://github.com/duma-repo/PyDyNet

git clone https://github.com/duma-repo/PyDyNet.git

LeNet 畳み込みを構築します。ニューラル ネットワーク、3 分類モデルをトレーニングします。

コード ファイルを PyDyNet ディレクトリに直接作成するだけです。

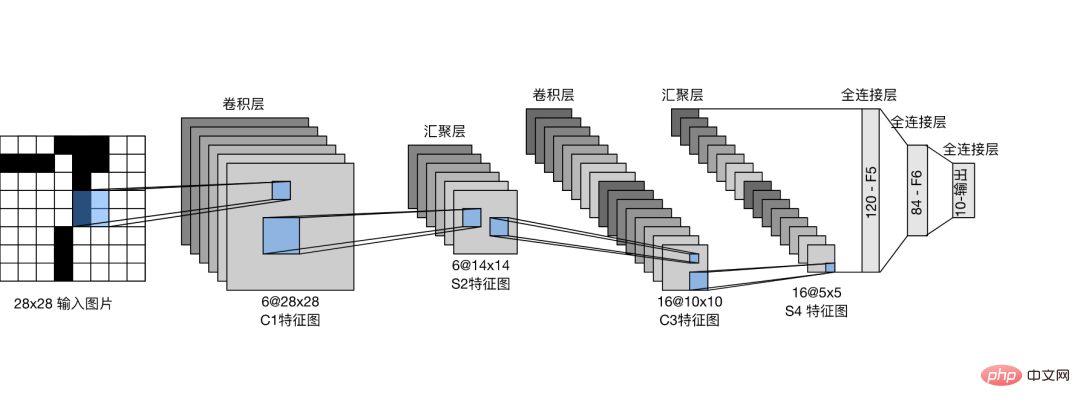
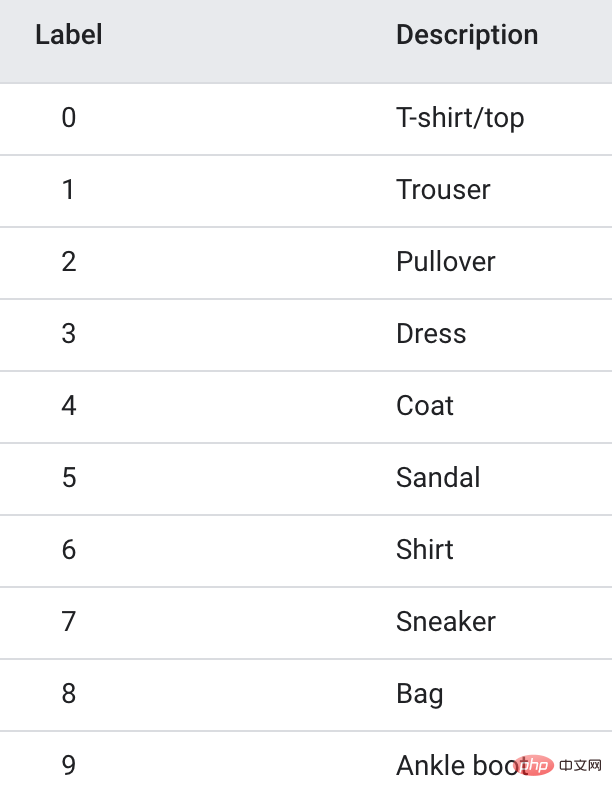
from pydynet import nn

class LeNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, kernel_size=5, padding=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.avg_pool = nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
self.sigmoid = nn.Sigmoid()
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 3)

def forward(self, x):
x = self.conv1(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = self.conv2(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = x.reshape(x.shape[0], -1)

x = self.fc1(x)
x = self.sigmoid(x)
x = self.fc2(x)
x = self.sigmoid(x)
x = self.fc3(x)

return x

ご覧のとおり、ネットワークの定義は Pytorch 構文とまったく同じです。

私が提供したソース コードでは、ネットワーク構造を出力するための summary 関数が提供されています。

1.2 データの準備

トレーニング データは Fanshion-MNIST データ セットを使用します。このデータ セットには、10 カテゴリの写真 (各カテゴリに 6,000 個の画像) が含まれています。

トレーニングを高速化するために、最初の 3 つのカテゴリ (合計 1.8 ワットのトレーニング画像) のみを抽出して 3 分類モデルを作成しました。

1.3 モデルのトレーニング

import pydynet
from pydynet import nn
from pydynet import optim

lr, num_epochs = 0.9, 10
optimizer = optim.SGD(net.parameters(),
lr=lr)
loss = nn.CrossEntropyLoss()

for epoch in range(num_epochs):
net.train()
for i, (X, y) in enumerate(train_iter):
optimizer.zero_grad()
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()

with pydynet.no_grad():
metric.add(l.numpy() * X.shape[0],
 accuracy(y_hat, y),
 X.shape[0])

トレーニング コードも Pytorch と同じです。

次に行うべき重要なことは、モデル トレーニングのソース コードを深く掘り下げて、モデル トレーニングの原則を学ぶことです。

2. train、no_grad、eval

モデルがトレーニングを開始する前に、net.train が呼び出されます。

def train(self, mode: bool = True):
set_grad_enabled(mode)
self.set_module_state(mode)

これにより、grad (gradient) が True に設定され、その後作成される Tensor に勾配を含めることができることがわかります。 Tensor が勾配をもたらした後、それは計算グラフに入れられ、勾配を計算するための導出を待ちます。

no_grad() を使用した次のコード: コード

class no_grad:
def __enter__(self) -> None:
self.prev = is_grad_enable()
set_grad_enabled(False)

は、grad (gradient) を False に設定します。これにより、後で作成された Tensor は計算グラフに配置されなくなります。勾配を計算する必要があるため、推論を高速化できます。

Pytorch で net.eval() が使用されているのをよく目にしますが、そのソース コードも見てみましょう。

def eval(self):
return self.train(False)

ご覧のとおり、train(False) を直接呼び出してグラデーションをオフにし、その効果は no_grad() と似ています。

したがって、通常はトレーニングの前に train を呼び出して勾配をオンにします。トレーニング後、 eval を呼び出して勾配を閉じ、高速な推論を容易にします。

3. 順伝播

カテゴリ確率の計算に加えて、順伝播で最も重要なことは、ネットワーク内のテンソルを順伝播の順序に従って計算グラフに整理することです。 . 目的 バックプロパゲーション中の各テンソルの勾配を計算するために使用されます。

ニューラル ネットワークでは、テンソルはデータを保存するためだけでなく、勾配を計算して保存するためにも使用されます。

最初の層の畳み込み演算を例として、計算グラフの生成方法を確認します。

def conv2d(x: tensor.Tensor,
 kernel: tensor.Tensor,
 padding: int = 0,
 stride: int = 1):
'''二维卷积函数
'''
N, _, _, _ = x.shape
out_channels, _, kernel_size, _ = kernel.shape
pad_x = __pad2d(x, padding)
col = __im2col2d(pad_x, kernel_size, stride)
out_h, out_w = col.shape[-2:]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
col_filter = kernel.reshape(out_channels, -1).T
out = col @ col_filter
return out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

#xx は入力画像であり、グラデーションを記録する必要はありません。カーネルはコンボリューション カーネルの重みであり、勾配を計算する必要があります。

したがって、pad_x = __pad2d(x, padding) によって生成される新しいテンソルにも勾配がないため、計算グラフに追加する必要はありません。

kernel.reshape(out_channels, -1) によって生成されたテンソルは勾配を計算する必要があり、計算グラフに追加する必要もあります。

結合プロセスを見てみましょう:

def reshape(self, *new_shape):
return reshape(self, new_shape)

class reshape(UnaryOperator):
'''
张量形状变换算子，在Tensor中进行重载

Parameters
----------
new_shape : tuple
变换后的形状，用法同NumPy
'''
def __init__(self, x: Tensor, new_shape: tuple) -> None:
self.new_shape = new_shape
super().__init__(x)

def forward(self, x: Tensor)
return x.data.reshape(self.new_shape)

def grad_fn(self, x: Tensor, grad: np.ndarray)
return grad.reshape(x.shape)

reshape 関数は reshape クラス オブジェクトを返します。reshape クラスは UnaryOperator クラスを継承し、 __init__ 関数で呼び出されます. 親クラスの初期化関数。

class UnaryOperator(Tensor):
def __init__(self, x: Tensor) -> None:
if not isinstance(x, Tensor):
x = Tensor(x)
self.device = x.device
super().__init__(
data=self.forward(x),
device=x.device,
# 这里 requires_grad 为 True
requires_grad=is_grad_enable() and x.requires_grad,
)

UnaryOperator クラスは Tensor クラスを継承するため、reshape オブジェクトも tensor です。

UnaryOperator の __init__ 関数では、Tensor の初期化関数が呼び出され、渡された required_grad パラメーターは True です。これは、勾配を計算する必要があることを意味します。

requires_grad 計算コードは is_grad_enable() と x.requires_grad で、is_grad_enable() は train によって True に設定されており、x はコンボリューション カーネルであり、その require_grad も True です。

class Tensor:
def __init__(
self,
data: Any,
dtype=None,
device: Union[Device, int, str, None] = None,
requires_grad: bool = False,
) -> None:
if self.requires_grad:
# 不需要求梯度的节点不出现在动态计算图中
Graph.add_node(self)

最後に、Tensor クラスの初期化メソッドで、Graph.add_node(self) を呼び出して、現在の tensor を計算グラフに追加します。

同様に、requires_grad=True を使用する次のテンソルで一般的に使用される新しいテンソルが計算グラフに配置されます。

畳み込み演算後、計算グラフに 6 つのノードが追加されます。

4. バックプロパゲーション

1 つの順伝播が完了したら、計算グラフの最後のノードから開始して、後ろから前にバックプロパゲーションを実行します。

l = loss(y_hat, y)
l.backward()

順方向ネットワークを通じて層ごとに伝播した後、最終的に損失テンソル l に送信されます。

l を始点として前から後ろに伝播すると、計算グラフの各ノードの勾配が計算できます。

backward のコア コードは次のとおりです。

def backward(self, retain_graph: bool = False):

for node in Graph.node_list[y_id::-1]:
grad = node.grad
for last in [l for l in node.last if l.requires_grad]:
add_grad = node.grad_fn(last, grad)

last.grad += add_grad

Graph.node_list[y_id::-1] は計算グラフを逆順に並べ替えます。

node​是前向传播时放入计算图​中的每个tensor。

node.last​ 是生成当前tensor的直接父节点。

调用node.grad_fn计算梯度，并反向传给它的父节点。

grad_fn​其实就是Tensor的求导公式，如：

class pow(BinaryOperator):
'''
幂运算算子，在Tensor类中进行重载

See also
--------
add : 加法算子
'''
def grad_fn(self, node: Tensor, grad: np.ndarray)
if node is self.last[0]:
return (self.data * self.last[1].data / node.data) * grad

return​后的代码其实就是幂函数求导公式。

假设y=x^2，x​的导数为2x。

5. 更新参数

反向传播计算梯度后，便可以调用优化器，更新模型参数。

l.backward()
optimizer.step()

本次训练我们用梯度下降SGD算法优化参数，更新过程如下：

def step(self):
for i in range(len(self.params)):
grad = self.params[i].grad + self.weight_decay * self.params[i].data
self.v[i] *= self.momentum
self.v[i] += self.lr * grad
self.params[i].data -= self.v[i]
if self.nesterov:
self.params[i].data -= self.lr * grad

self.params​是整个网络的权重，初始化SGD时传进去的。

step​函数最核心的两行代码，self.v[i] += self.lr * grad​ 和 self.params[i].data -= self.v[i]​，用当前参数 - 学习速率 * 梯度​更新当前参数。

这是机器学习的基础内容了，我们应该很熟悉了。

一次模型训练的完整过程大致就串完了，大家可以设置打印语句，或者通过DEBUG的方式跟踪每一行代码的执行过程，这样可以更了解模型的训练过程。

以上が信じられない！ Numpy を使用して深層学習フレームワークを開発し、ニューラル ネットワークのトレーニング プロセスを調査するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。