ホームページ >テクノロジー周辺機器 >AI >AI は数学データベースの問題の 82% を証明できます。新しい SOTA は達成されており、現在も Transformer に基づいています。
AI は数学データベースの問題の 82% を証明できます。新しい SOTA は達成されており、現在も Transformer に基づいています。
- 王林転載
- 2023-04-10 08:51:08939ブラウズ

科学者たちは最近、AI に数学の授業を与えることに夢中になっていると言わざるを得ません。
いいえ、Facebook チームもこの楽しみに参加し、定理の実証を完全に自動化でき、SOTA よりも大幅に優れた新しいモデルを提案しました。
数学の定理が複雑になるにつれて、人間の力だけで定理を証明することはますます困難になることを知っておく必要があります。
したがって、コンピューターを使用して数学の定理を実証することが研究の焦点になっています。
OpenAI は以前、この方向に特化したモデル GPT-f を提案しました。これにより、メタマスの問題の 56% を実証できます。
今回提案された最新の手法では、この数字を82.6%まで高めることが可能です。
同時に、研究者らは、この方法は GPT-f に比べて時間がかからず、コンピューティング消費量を元の 10 分の 1 に削減できると述べています。
今度は AI が数学との戦いに成功すると言えるでしょうか?
それとも Transformer
この記事で提案する手法は、Transformer に基づいたオンライン トレーニング プログラムです。
は、大きく 3 つのステップに分けることができます:
最初の 、数学的証明ライブラリでの事前トレーニング;
2 つ目 、教師付きデータ セットでポリシー モデルを微調整します。
#3 番目 、ポリシー モデルと判断モデルのオンライン トレーニング。
具体的には、検索アルゴリズムを使用してモデルに既存の数学的証明ライブラリから学習させ、さらに多くの問題を促進および証明します。
数学的証明ライブラリには、Metamath、Lean、および自社開発の証明環境の 3 種類が含まれます。
簡単に言えば、これらの証明ライブラリは、通常の数学言語をプログラミング言語に似た形式に変換します。
Metamath のメイン ライブラリは set.mm で、これには ZFC 集合論に基づいた約 38,000 の証明が含まれています。
Lean は、IMO コンテストに参加できる Microsoft の AI アルゴリズムとしてよく知られています。 Lean ライブラリは、同じ名前のアルゴリズムに学部数学の知識をすべて教え、これらの定理の証明を学習させるように設計されています。
この研究の主な目標は、問題を証明するための一連の適切な戦略を自動的に生成できる証明者を構築することです。
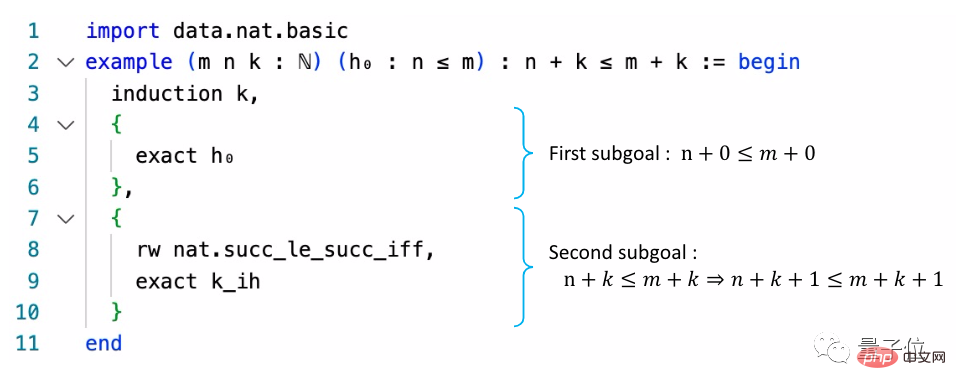
この目的を達成するために、研究者らは、MCTS に基づく非平衡ハイパーグラフ証明探索アルゴリズムを提案しました。
MCTS は、Monte Carlo Tree Search と訳され、ゲーム ツリーの問題を解決するためによく使用され、AlphaGo でよく知られています。
その動作プロセスは、検索空間内でランダムにサンプリングすることによって有望なアクションを見つけ、このアクションに基づいて検索ツリーを拡張することです。
この研究で採用されたアイデアはこれに似ています。
検索証明プロセスは、ゴール g から始まり、メソッドを下方向に検索し、徐々にハイパーグラフに発展します。
空の集合が分岐の下に現れる場合、それは最適な証明が見つかったことを意味します。
最後に、バックプロパゲーションプロセス中に、ノード値とスーパーツリーの総操作数を記録します。
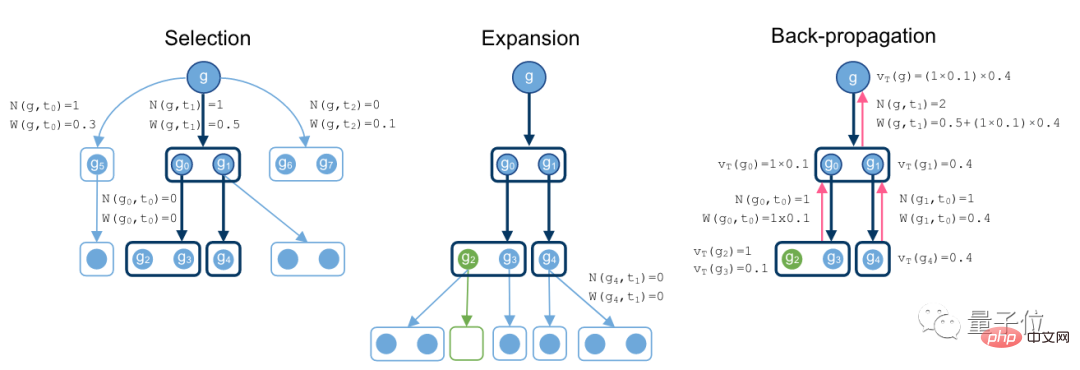
このリンクでは、研究者は戦略モデルと判断モデルを想定しました。
戦略モデルでは、判断モデルによるサンプリングが可能で、証明方法を見つける現在の戦略の能力を評価できます。
検索アルゴリズム全体は、上記の 2 つのモデルを参照として使用します。
これら 2 つのモデルは Transformer モデルであり、重みを共有しています。
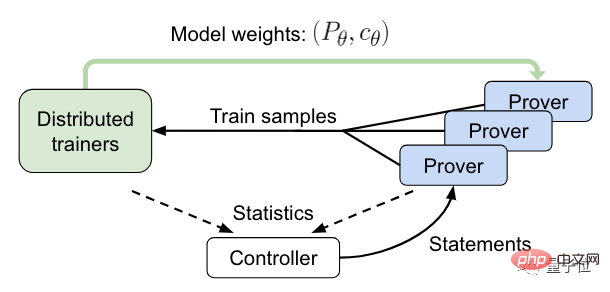
次に、オンライン トレーニングの段階です。
このプロセスでは、コントローラーはステートメントを非同期 HTPS 検証に送信し、トレーニング データと証明データを収集します。
その後、バリデーターはトレーニング サンプルを分散トレーナーに送信し、そのモデルのコピーを定期的に同期します。
実験結果
テストセッションでは、研究者らはHTPSとGPT-fを比較しました。
後者は、OpenAI によって以前に提案された数学的定理推論モデルであり、これも Transformer に基づいています。
結果は、オンライン トレーニング後のモデルがメタマスの問題の 82% を証明できることを示しており、GPT-f の以前の記録である 56.5% をはるかに上回っています。

リーン ライブラリでは、このモデルは定理の 43% を証明できますが、これは SOTA よりも 38% 高いです。以下は、このモデルによって証明された IMO テストの問題です。

#しかし、まだ完璧ではありません。
たとえば、次の質問では、最も単純な方法では質問が解決されませんでしたが、研究者らは、これは注釈のエラーが原因であると述べました。

One More Thing
コンピューターを使用して数学の問題を実証する、4 色定理の証明は、最もよく知られた例の 1 つです。
4 色定理とは、現代数学の 3 つの主要な問題の 1 つで、「どの地図でも、共通の国境を持つ国々を異なる色で着色するために使用できるのは 4 色のみである」というものです。
この定理の実証には多くの計算が必要なため、提案されてから 100 年以内に誰も完全に実証できませんでした。
1976 年まで、イリノイ大学の 2 台のコンピューターで 1,200 時間と 100 億回の判断を行った後、ついに、どんな地図でもマークするには 4 色だけが必要であることを実証することができました。これは数学界全体にセンセーションを巻き起こしました。コミュニティ。
さらに、数学の問題が複雑になるにつれて、定理が正しいかどうかを人力でチェックすることが難しくなります。
最近、AI コミュニティは徐々に数学の問題に焦点を当てるようになりました。
2020 年、OpenAI は、自動定理証明に使用できる数学的定理推論モデル GPT-f を発表しました。
この方法では、テスト セット内の証明の 56.5% を完了でき、当時の SOTA モデル MetaGen-IL を 30% 以上上回っています。
同じ年、Microsoft は IMO テストの問題を作成できる Lean もリリースしました。これは、AI がこれまで見たことのない問題を作成できることを意味します。
昨年、OpenAI が GPT-3 に検証機能を追加した後、数学の問題を行う効果は以前の微調整方法よりも大幅に向上し、小学生のレベルの 90% に達する可能性がありました。
今年 1 月、MIT、ハーバード大学、コロンビア大学、ウォータールー大学の共同研究により、彼らが提案したモデルが高度な数学を実行できることが示されました。
つまり、科学者たちは部分的なテーマである AI を文系と理系の両方にしようと懸命に取り組んでいるのです。
以上がAI は数学データベースの問題の 82% を証明できます。新しい SOTA は達成されており、現在も Transformer に基づいています。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

