ホームページ >バックエンド開発 >Python チュートリアル >Python のデータ構造とアルゴリズム学習の両端キュー
Python のデータ構造とアルゴリズム学習の両端キュー
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2022-04-01 12:09:293171ブラウズ
この記事では、python に関する関連知識を提供します。主に、両端キューの基本概念、両端キューの実装、二重端キューなど、両端キューに関連する問題を紹介します。終了キュー. 終了キューの応用、皆さんのお役に立てれば幸いです。

推奨学習: python チュートリアル
0. 学習目標
両端キューも線形データです構造。制限付き線形テーブルでもありますが、スタックやキューとは異なり、両端キューにはほとんど制限がありません。基本的な演算も線形テーブル演算のサブセットですが、データ型の観点からは、線形テーブルとは大きく異なります。違う。このセクションでは、両端キューの定義とそのさまざまな実装を紹介し、両端キューの実際のアプリケーションをいくつか示します。
このセクションを学習することで、次の内容を習得する必要があります:
- ダブルエンド キューの基本概念とさまざまな実装方法
- double の基本操作の実装と時間の計算量両端キュー
- 両端キューの基本操作を使用して複雑なアルゴリズムを実装する
1. 両端キューの基本概念
1.1両端キューの基本概念
両端キュー (double-end queue, deque) も、挿入と削除が行われる線形リストです。操作はシーケンスの両端に制限されますが、スタックやキューとは異なります。違いは、両端のキューにはほとんど制限がないことです。両端のキューの場合、末尾 (rear) と先頭 (#) の両方が制限されます。 ##front) 要素の挿入と削除を許可します。新しい要素はキューの先頭または末尾に追加できます。同様に、既存の要素はどちらの端からも削除できます。ある意味、両端キューはスタックとキューの組み合わせと考えることができます。
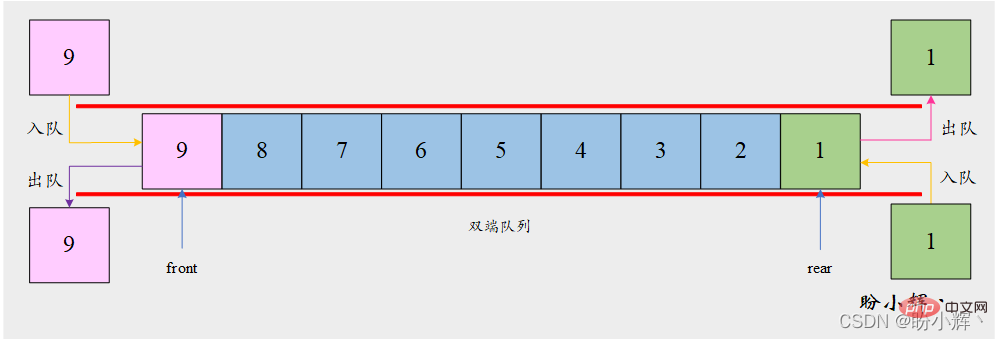
LIFO 原則と制限に従う必要はありません。構造体 FIFO 主演算要素。
1.2 両端キューの抽象データ型
両端キューには要素の追加や削除の他に、初期化、キュー空判定などの補助的な操作もあります。 、およびキューの長さの決定。具体的には、両端キューの抽象データ型は次のように定義されます。基本操作:#2. 両端キューの実装通常のキューと同様に、両端キューにもシーケンシャル ストレージとチェーン ストレージの 2 つのストレージ表現方法があります。 。1. __itit__(): 両端キューを初期化します
空の両端キューを作成します
〜 2. size(): 両端キューに含まれる要素の数 n
を取得して返します 〜 〜 両端キューが空の場合は、整数 0
を返します 〜 〜 3. isempty ():空かどうか判定 終了キュー
要素が両端キューに格納されているか判定
4. addfront(data): 両端キューの先頭に要素を追加
キューの先頭に要素データを挿入します
5. addrear(data):Double 両端キューの最後に要素を追加します
キューの最後に要素データを挿入します
6.removefront (): 両端キューの先頭要素を削除します
先頭要素を削除して返します
7.removerear(): 両端キューの末尾要素を削除します
〜 〜を削除して返しますtail 要素
2.1 シーケンシャル ダブルエンド キューの実装
シーケンシャル キューと同様に、ダブルエンド キューのシーケンシャル ストレージ構造では、連続するストレージ ユニットのセットを使用します。両端キューのデータを順番に格納するためのアドレスであり、キューの先頭から両端キューの末尾までの要素のうち、frontとrearという2つのポインタが存在します。キューの先頭要素とキューの末尾要素の位置をそれぞれ示すために必要です。空の両端キューを初期化する場合、front=rear=0、要素がキューに入るとき、rear は 1 増加し、要素がデキューされるとき、front は増加します。 1 により、空き領域を再利用するために、連続両端キューには末尾リング領域があると仮定し、最後のスペースと最初のスペースは連続したスペースとみなされます (具体的な理由については、 を参照してください) ):
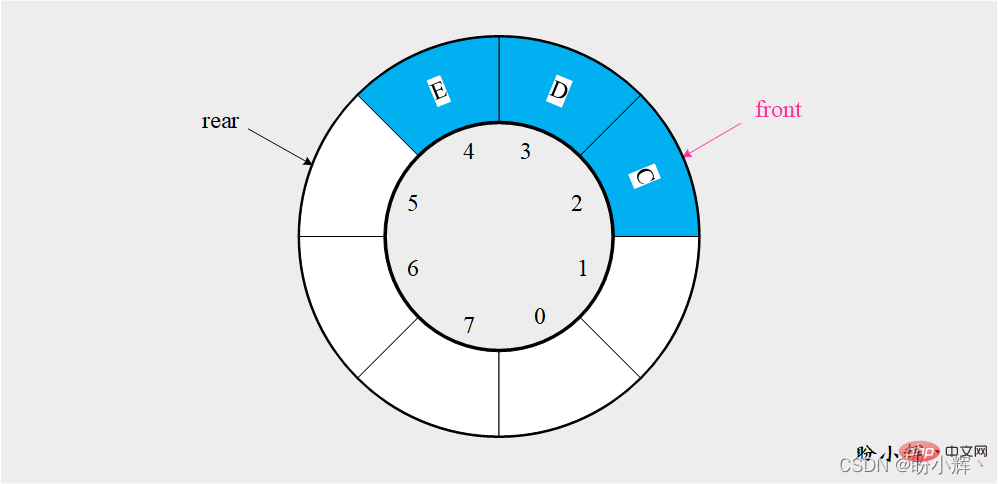
2.1.1 両端キューの初期化
シーケンシャル両端キューの初期化には 4 つの情報が必要です:deque リストが使用されますデータ要素を保存するには、max_size を使用して queue リストの最大長を保存し、front と rear を使用して記録します。それぞれキューの先頭要素と末尾要素。インデックス:
class Deque: def __init__(self, max_size=6): self.max_size = max_size self.deque = [None] * self.max_size self.front = 0 self.rear = 0
2.1.2 両端のキューの長さを確認します
front と rear はヘッドの記録に使用されるため、それぞれ要素と末尾要素 要素のインデックス。これにより、両端キューの長さを簡単に計算できます。同時に、両端キューが循環キューであることを考慮する必要があります (front#) ## は rear より大きい可能性があり、rear-front を直接渡すことはできません。この問題を解決するには、数式計算を使用する必要があります:
Python 実装は以下の通りです。
def size(self): return (self.rear-self.front+self.max_size) % self.max_size
2.1.3 両端キューが空かどうかの判定
両端キューかどうかを簡単に判定できます。front と rear の値に基づいて、キューは空です:
def isempty(self): return self.rear==self.front
2.1.4 両端キューが満杯であることの判断
front と rear の値に従って、両端のキューに空き領域があるかどうかを簡単に判断できます:
def isfull(self): return ((self.rear+1) % self.max_size == self.front)2.1.5 両端キューの先頭と末尾に要素を追加する要素を追加するときは、まず両端キューに空き領域があるかどうかを確認し、次に、ロング シーケンシャル デキューまたは動的シーケンシャル デキューに応じて両端キューのサイズが異なる場合、要素を追加する操作は若干異なります。
[固定長シーケンシャル デキューの要素追加操作]キューがいっぱいの場合、例外がスローされます:
# 注意队头和队尾修改索引的添加元素的不同顺序
def addrear(self, data):
if not self.isfull():
self.deque[self.rear] = data
self.rear = (self.rear+1) % self.max_size else:
raise IndexError("Full Deque Exception")
def addfront(self, data):
if self.isfull():
self.resize()
if self.isempty():
# 当Python のデータ構造とアルゴリズム学習の両端キュー
self.deque[self.rear] = data
self.rear = (self.rear+1) % self.max_size else:
self.front = (self.front - 1 + self.max_size) % self.max_size
self.deque[self.front] = data
[動的シーケンスの両端キューの要素追加操作] 両端キューがいっぱいの場合は、最初に新しいスペースを申請し、次に、追加操作を実行します:
def resize(self): new_size = 2 * self.max_size new_deque = [None] * new_size d = new_size - self.max_size for i in range(self.max_size): new_deque[(self.front+i+d) % new_size] = self.deque[(self.front+i) % self.max_size] self.deque = new_deque self.front = (self.front+d) % new_size self.max_size = new_size # 注意队头和队尾修改索引的添加元素的不同顺序 def addrear(self, data): if self.isfull(): self.resize() self.deque[self.rear] = data self.rear = (self.rear+1) % self.max_size def addfront(self, data): if self.isfull(): self.resize() self.front = (self.front - 1 + self.max_size) % self.max_size self.deque[self.front] = data動的シーケンスの場合 キューと同様に、コピー後のインデックスも考慮する必要があります。そうしないと、使用できない空き領域が生じる可能性があります:
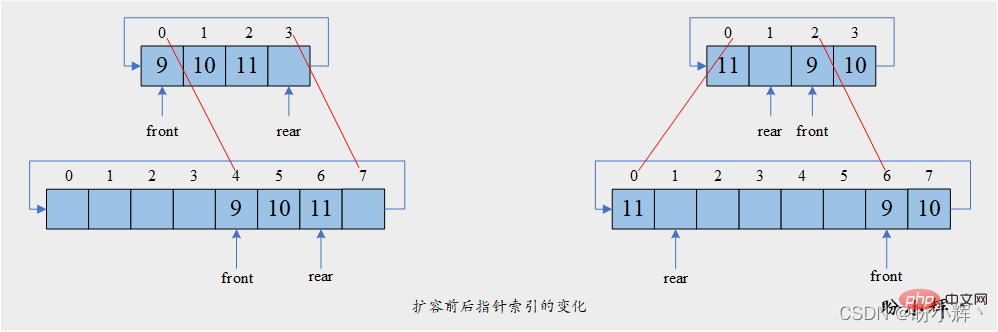
O(1) 。ただし、動的シーケンシャル両端キューがいっぱいの場合は、元の両端キューの要素を最初に新しい両端キューにコピーしてから、新しい要素を追加する必要があります。ただし、シーケンシャル キューの概要を参照してください。 「シーケンス テーブルとその操作の実装」のテーブル追加操作。 #n 要素追加操作の合計時間のため #T(n) および O(n) は正比例するため、その償却時間計算量は考慮できます#O(1)。 2.1.6 キューの先頭または末尾の要素を削除します。
両端キューが空でない場合は、指定された位置にある要素を削除して返します。 end: # 注意队头和队尾修改索引的删除元素的不同顺序
def removefront(self):
if not self.isempty():
result = self.deque[self.front]
self.front = (self.front+1) % self.max_size return result else:
raise IndexError("Empty Deque Exception")
def removerear(self):
if not self.isempty():
self.rear = (self.rear - 1 + self.max_size) % self.max_size
result = self.deque[self.rear]
return result else:
raise IndexError("Empty Deque Exception")
2.2 連鎖両端キューの実装
両端キューの別のストレージ表現は、連鎖ストレージ構造を使用することです。多くの場合、連鎖両端キューと呼ばれます。addfront
操作とaddrear 操作は、それぞれリンク リストの先頭と末尾に要素を挿入することによって実装されます。一方、 Removefront 操作と removerear 操作はそれぞれ、先頭と末尾からノードを削除することによって実現されます。末尾のノードを削除する時間の複雑さを軽減するために、二重リンク リストに基づいて両端キューが実装されます。
2.2.1 両端キュー ノード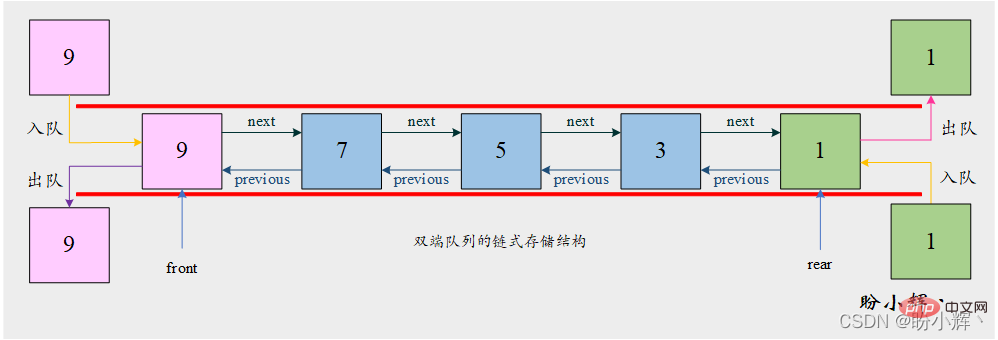
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
def __str__(self):
return str(self.data)
2.2.2 両端キューの初期化 両端キューの初期化関数では、先頭ポインタを front
、末尾ポインタをrear にします。 両方とも None を指し、両端のキューの長さを初期化します。
class Deque: def __init__(self): self.front = None self.rear = None self.num = 0
2.2.3 両端のキューの長さの確認 num
の値を返して、両端のキューの長さを確認します。キューの長さによって、それが空の両端のキューであるかどうかを簡単に判断できます:def size(self): return self.num
2.2 .5 要素の追加 両端のキューに要素を追加する場合、キューの最後または先頭に新しい要素を挿入できるため、rear および を変更する必要があります。 front
ポインタ、およびノードのnext
およびprevious
ポインタも変更します; 要素を追加する場合 前の両端キューは空なので、それに応じて処理する必要があります:def addrear(self, data): node = Node(data) # 如果添加元素前Python のデータ構造とアルゴリズム学習の両端キュー为空,则添加结点时,需要将front指针也指向该结点 if self.front is None: self.rear = node self.front = node else: node.previous = self.rear self.rear.next = node self.rear = node self.num += 1 def addfront(self, data): node = Node(data) # 如果添加元素前Python のデータ構造とアルゴリズム学習の両端キュー为空,则添加结点时,需要将rear指针也指向该结点 if self.rear is None: self.front = node self.rear = node else: node.next = self.front self.front.previous = node self.front = node self.num += 1
2.2.6 删除元素
若Python のデータ構造とアルゴリズム学習の両端キュー不空,可以从删除队头或队尾元素并返回,删除操作需要更新队头指针 front 以及尾指针 rear,同时也要修改结点的 next 和 previous 指针,若出队元素尾队中最后一个结点,还需要进行相应处理:
def removefront(self):
if self.isempty():
raise IndexError("Empty Queue Exception")
result = self.front.data
self.front = self.front.next
self.num -= 1
if self.isempty():
self.rear = self.front else:
# 若删除操作完成后,Python のデータ構造とアルゴリズム学習の両端キュー不为空,将 front 指针的前驱指针指向 None
self.front.previous = None
return result
def removerear(self):
if self.isempty():
raise IndexError("Empty Queue Exception")
result = self.rear.data
self.rear = self.rear.previous
self.num -= 1
if self.isempty():
self.front = self.rear else:
# 若删除操作完成后,Python のデータ構造とアルゴリズム学習の両端キュー不为空,将 rear 指针的后继指针指向 None
self.rear.next = None
return result
2.3 Python のデータ構造とアルゴリズム学習の両端キュー的不同实现对比
Python のデータ構造とアルゴリズム学習の両端キュー的不同实现对比与栈的不同实现类似,可以参考《栈及其操作实现》。
3. Python のデータ構造とアルゴリズム学習の両端キュー应用
接下来,我们首先测试上述实现的Python のデータ構造とアルゴリズム学習の両端キュー,以验证操作的有效性,然后利用实现的基本操作来解决实际算法问题。
3.1 顺序Python のデータ構造とアルゴリズム学習の両端キュー的应用
首先初始化一个顺序Python のデータ構造とアルゴリズム学習の両端キュー deque,然后测试相关操作:
# 初始化一个最大长度为5的Python のデータ構造とアルゴリズム学習の両端キューdq = Deque(5)print('Python のデータ構造とアルゴリズム学習の両端キュー空?', dq.isempty())for i in range(3):
print('队头添加元素:', 2*i)
dq.addfront(2*i)
print('队尾添加元素:', 2*i+1)
dq.addrear(2*i+1)print('Python のデータ構造とアルゴリズム学習の両端キュー长度为:', dq.size())for i in range(3):
print('队尾删除元素:', dq.removerear())
print('队头删除元素:', dq.removefront())print('Python のデータ構造とアルゴリズム学習の両端キュー长度为:', dq.size())
测试程序输出结果如下:
Python のデータ構造とアルゴリズム学習の両端キュー空? True队头添加元素: 0队尾添加元素: 1队头添加元素: 2队尾添加元素: 3队头添加元素: 4队尾添加元素: 5Python のデータ構造とアルゴリズム学習の両端キュー长度为: 6队尾删除元素: 5队头删除元素: 4队尾删除元素: 3队头删除元素: 2队尾删除元素: 1队头删除元素: 0Python のデータ構造とアルゴリズム学習の両端キュー长度为: 0
3.2 链Python のデータ構造とアルゴリズム学習の両端キュー的应用
首先初始化一个链Python のデータ構造とアルゴリズム学習の両端キュー queue,然后测试相关操作:
# 初始化新队列dq = Deque()print('Python のデータ構造とアルゴリズム学習の両端キュー空?', dq.isempty())for i in range(3):
print('队头添加元素:', i)
dq.addfront(2*i)
print('队尾添加元素:', i+3)
dq.addrear(2*i+1)print('Python のデータ構造とアルゴリズム学習の両端キュー长度为:', dq.size())for i in range(3):
print('队尾删除元素:', dq.removerear())
print('队头删除元素:', dq.removefront())print('Python のデータ構造とアルゴリズム学習の両端キュー长度为:', dq.size())
测试程序输出结果如下:
Python のデータ構造とアルゴリズム学習の両端キュー空? True队头添加元素: 0队尾添加元素: 3队头添加元素: 1队尾添加元素: 4队头添加元素: 2队尾添加元素: 5Python のデータ構造とアルゴリズム学習の両端キュー长度为: 6队尾删除元素: 5队头删除元素: 4队尾删除元素: 3队头删除元素: 2队尾删除元素: 1队头删除元素: 0Python のデータ構造とアルゴリズム学習の両端キュー长度为: 0
3.3 利用Python のデータ構造とアルゴリズム学習の両端キュー基本操作实现复杂算法
[1] 给定一字符串 string (如:abamaba),检查其是否为回文。
使用Python のデータ構造とアルゴリズム学習の両端キュー可以快速检查一字符串是否为回文序列,只需要将字符串中字符依次入队,然后从Python のデータ構造とアルゴリズム学習の両端キュー两端依次弹出元素,对比它们是否相等:
def ispalindrome(string): deque = Deque() for ch in string: deque.addfront(ch) flag = True while deque.size() > 1 and flag: ch1 = deque.removefront() ch2 = deque.removerear() if ch1 != ch2: flag = False return flag
验证算法有效性:
print('abcba是否为回文序列:', ispalindrome('abcba'))print('charaahc是否为回文序列:', ispalindrome('charaahc'))
结果输出如下:
abcba是否为回文序列: True charaahc是否为回文序列: False
推荐学习:python教程
以上がPython のデータ構造とアルゴリズム学習の両端キューの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

