バイナリツリートラバーサルと論理演算方法の詳細な説明
- 醉折花枝作酒筹転載
- 2021-07-26 17:43:341737ブラウズ
まず第一に、二分木は木の最も典型的な応用であるため、私たちの研究の主な内容は二分木であることをまだ説明する必要があります。必ず学ばなければならない内容。

まず、ツリーの操作を学ぶ前に、ツリーの操作の中心は「走査」であることを理解する必要があります。なぜそんなことを言うのですか?スタックやキューとは異なり、ツリー構造は実際には 1 次元ではなく、枝があり、さまざまな角度があり、さらに重要なことに、階層の概念があります。
1 次元空間にあるものは、私たちの共通の「線」であり、長さのみで高さはなく、この長さが唯一の次元です。スタックとキューは明らかに 1 次元です。ツリーは異なりますが、階層の概念により「高さ」、つまり 2 次元の概念にアップグレードされています。前回の記事で紹介した名詞の束と同じように、木の高さ(奥行き)という概念があります。
ツリーを走査できるようになったら、走査に基づいてツリーのノードに対して追加、削除、変更などの操作を行うことができます。これらの基本的な論理操作はすべて走査に基づいています。上記をよく考えてください。スタックとキューについてですが、実はそれらの論理演算もトラバーサルから始まるのではないでしょうか?ポップするかスタックに入るか、デキューするかエンキューするかにかかわらず、私たちはすべて固定トラバーサル ルール (FILO、FIFO) に基づいています。
二次元のものは、それをどう横断するかがポイントになります。 1 次元のデータ構造を順番に走査するだけで済みますが、2 次元のデータ結果は単純に 1 つずつ順番に走査することはできません。これは、ノード間に階層関係があるためです。したがって、ノードに階層関係がない場合は、現在のデータ構造を考慮する必要があります。子ノード、トラバーサル操作中に何をすべきでしょうか?
幸いなことに、私たちは巨人の肩の上に立つことでこの知識を学びます。多くの先輩が非常に簡単なツリートラバース方法をいくつかまとめてくれています。まずは本題から外して、ツリーの構築方法を見てみましょう。これは、前の記事で示したバイナリ ツリーです。
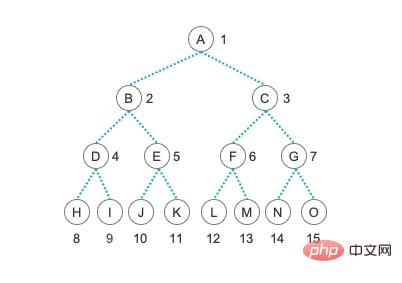
バイナリ ツリーの連鎖ストレージ構造
バイナリ ツリーの連鎖ストレージの使用は、非常にシンプルで非常に視覚的です。皆さん、バイナリの逐次ストレージを片付けましょう。というのは、次の記事で、シーケンシャル ストレージがどのような状況で使用されるかを説明するからです。
class BiTree
{
public $data;
public $lChild;
public $rChild;
}実際、チェーン ストレージでは、ノードを 1 つずつ使用してツリーを保存します。各バイナリ ツリー ノードには、データ属性であるデータ フィールドがあります。他の 2 つの属性は、2 つのフォークされたポインター、つまりこのノードの左側の子ノード lChild と右側の子ノード rChild とみなすことができます。
スタックとキューの比較は、次のノードを左右の子ノードに置き換えただけであり、本質的にはスタックとキューと大きな違いはありません。率直に言うと、データ構造の観点から見ると、私たちは依然として 2 次元の概念を表すために 1 次元のストレージを使用しており、この概念の変換には、概念的な理解の観点から始める必要があります。
二分木の構築
// 建立二叉树
function CreateBiTree($arr, $i)
{
if (!isset($arr[$i])) {
return null;
}
$t = new BiTree();
$t->data = $arr[$i];
$t->lChild = CreateBiTree($arr, $i * 2);
$t->rChild = CreateBiTree($arr, $i * 2 + 1);
return $t;
}このような簡単な方法で、連鎖二分木の構築を完了することができます。皆さん、注意して見てください。この単純なツリー構築操作には、実際には多くの謎が含まれています:
配列を使用してツリーの各ノードを順番に表します。たとえば、「A」と入力します。順に、B、C、D、E... (ツリーの順次ストレージで再度確認します)
割り当ての内容は、現在のデータです。 $i 添字、左右の子に値を代入する際に再帰的な操作が行われたことに注意してください
スタックを学習する際、「再帰」がスタックであることを学習しました-type 操作なので、このコードではスタックの形式でツリーを構築します
毎回 i 2 と i 2 1 に気づきましたか?バイナリ ツリーのプロパティを確認してください。 5
最後に、このメソッドがリンク ツリー構造を正常に構築できるかどうかをテストします。
$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O']; $tree = CreateBiTree($treeList, 1); print_r($tree); // BiTree Object // ( // [data] => A // [lChild] => BiTree Object // ( // [data] => B // [lChild] => BiTree Object // ( // [data] => D // [lChild] => BiTree Object // ( // [data] => H // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => I // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => E // [lChild] => BiTree Object // ( // [data] => J // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => K // [lChild] => // [rChild] => // ) // ) // ) // [rChild] => BiTree Object // ( // [data] => C // [lChild] => BiTree Object // ( // [data] => F // [lChild] => BiTree Object // ( // [data] => L // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => M // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => G // [lChild] => BiTree Object // ( // [data] => N // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => O // [lChild] => // [rChild] => // ) // ) // ) // )
印刷内容は非常に明確である必要がありますね。ノード A には、左右に 2 つの子ノード、つまり B と C があります。ノード B には、左右に 2 つの子ノード、つまり D と E があります。最終的な構造は、上記の二分木図の構造とまったく同じです。ここでは、渡された配列の最初の要素、つまり添字が 0 のデータを空にし、2 番目の要素、つまり要素から始まるツリーを構築するという事実にも注意する必要があります。下付き文字が 1 の場合。これは、バイナリ ツリーのプロパティ 5 を直感的かつ便利に使用して、このツリーを迅速に構築できるようにするためでもあります。
二叉树的遍历
说完二叉树的建树了,其实我们就已经接触到了一种二叉树的遍历形式。注意看我们建树方法中的代码,我们是先给结点的 data 赋值,然后建立这个结点的左、右孩子结点,并为它们赋值后再继续使用同样的操作一路建立完成所有的结点。现在,我们将这个操作反过来,不是建立结点,而是读取这些结点的内容,先读取结点的内容,然后再读取这个结点左右孩子结点的内容,这就是“先序遍历”。
先序遍历
/**
* 前序遍历
*/
function PreOrderTraverse(?BiTree $t)
{
if ($t) {
echo $t->data, ',';
PreOrderTraverse($t->lChild);
PreOrderTraverse($t->rChild);
}
}
PreOrderTraverse($tree);
// A,B,D,H,I,E,J,K,C,F,L,M,G,N,O,是不是很神奇?就连建树我们竟然也使用的是同一种遍历的方法,可以看出对于二叉树这种复杂的数据结构来说,遍历的重要作用了吧。
大家可以看一个遍历读取出来的结点顺序,貌似和我们输入的顺序不一样呀!没错,先序遍历是通过递归,先按一个方向走到底,当这个结点没有子结点之后,通过递归栈的特性再向上弹出。并且在遍历孩子结点之前先输出当前这个结点的内容。注意,这一句话很重要!所以我们的顺序就是 A,B,D,H ,当 H 没有子结点之后,我们就回到父结点 D 再进入它的右子结点 I ,具体顺序可以参考下图:
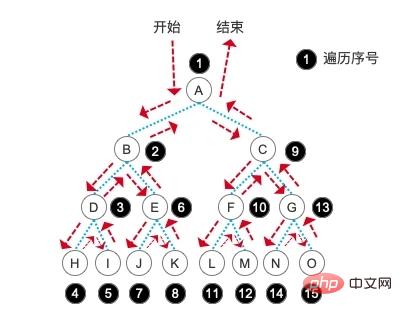
我们代码中的先序遍历和先序建树的结点顺序是完全不一样的,这一点也是要搞清楚的。建树的过程我们根据二叉树的 性质5 直接为它指定了数据下标。而在遍历过程中则是一个结点一个结点的去扫描遍历整颗树的。
中序遍历
顾名思义,中序遍历其实就是在遍历完左孩子结点之后再输出当前这个结点的内容,所以我们只需要微调先序遍历的代码即可。
/**
* 中序遍历
*/
function InOrderTraverse(?BiTree $t)
{
if ($t) {
InOrderTraverse($t->lChild);
echo $t->data, ',';
InOrderTraverse($t->rChild);
}
}
InOrderTraverse($tree);
// H,D,I,B,J,E,K,A,L,F,M,C,N,G,O,中序遍历的步骤就是我们会直接先走到最左边的子结点,当遇到最后一个结点时,输出内容,也就是图中的 H 结点,接着回到它的父结点 D 结点,这时根据中序的原理输出 D ,再进入它的右孩子结点并输出 I 。
D 结点的子树及它本身遍历完成后,返回 D 结点的上级结点 B 结点,输出 B ,然后进入 B 结点的右孩子结点 E 。再次进入到 E 的最左孩子结点 J ,然后参考 D 结点的遍历形式完成整颗树的遍历。具体顺序参考下图:
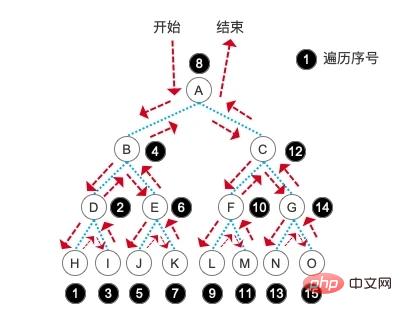
后序遍历
在学习了先序和中序之后,从名字就可以看出来后序就是在遍历完一个结点的左右孩子之后最后输出这个结点的内容,代码当然也是简单地微调一下就可以了。
/**
* 后序遍历
*/
function PostOrderTraverse(?BiTree $t)
{
if ($t) {
PostOrderTraverse($t->lChild);
PostOrderTraverse($t->rChild);
echo $t->data, ',';
}
}
PostOrderTraverse($tree);
// H,I,D,J,K,E,B,L,M,F,N,O,G,C,A,具体原理就不详细说明了,相信在学习了先序和中序之后,你一定能马上想明白后序遍历到底是什么意思了。直接上图:
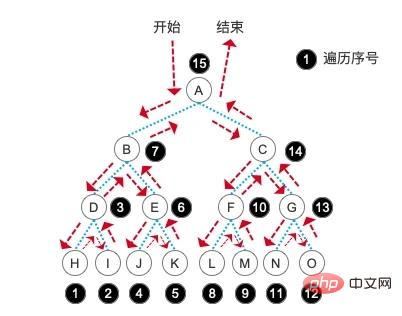
层序遍历
最后,我们要讲的就是层序遍历。既然有“层”这个关键字了,相信大家马上就能联想到,是不是一层一层地去遍历啊!没错,层序遍历就是这个意思,我们按照树的层次,一层一层地输出相应的结点信息。需要注意的,在这里我们会用到队列,而不是栈了。
/**
* 层序遍历
*/
$q = InitLinkQueue();
function LevelOrderTraverse(?BiTree $t)
{
global $q;
if (!$t) {
return;
}
EnLinkQueue($q, $t);
$node = $q;
while ($node) {
$node = DeLinkQueue($q);
if ($node->lChild) {
EnLinkQueue($q, $node->lChild);
}
if ($node->rChild) {
EnLinkQueue($q, $node->rChild);
}
echo $node->data, ',';
}
}
LevelOrderTraverse($tree);
// A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,InitLinkQueue() EnLinkQueue() 、 EnLinkQueue() 这些都是我们之前学习队列的时候所写的对于队列的逻辑操作方法。是不是很开心呀,之前的知识又用上了。层序遍历的核心思想就是运用队列的概念,遇到一个结点,就把这个结点入队,然后判断它是否有子结点,然后相继把子结点入队。
每遍历一个结点,就把队首的结点出队,这样就完成了按树的层次遍历的能力。文字说明还是太抽象,我们还是通过图片来展示这一过程:
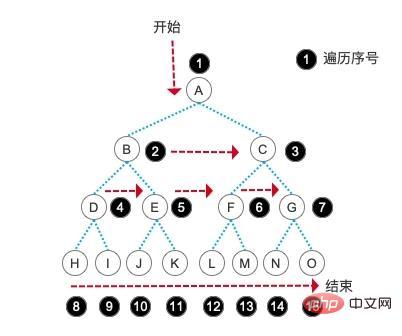
大家有没有发现,层序遍历的输出结果就和我们建树时的数组顺序完全相同了。很好玩吧,所以说代码的世界总是有无穷的乐趣等着我们去发现哦!
总结
今天的内容有没有懵圈?如果懵圈了就多找资料好好研究一下,先序、中序、后序都是利用栈来进行树的结点遍历的,而层序遍历则是利用了队列。一环套一环呀,前面学习的内容都派上用场了吧!不过这只是个开始,在学习图的时候,我们会在深度遍历和广度遍历中再次看到栈和队列的身影,它们可都是亲戚哦。
这四种遍历方式在考试和面试中也是经常出现的,不管是它们的原理还是画图或者是根据图形来写出各种遍历的顺序,都是非常常见的考核内容,所以大家在这篇文章入门的基础上还是要更加深入的去根据一些教材来深入的理解这几种遍历,熟练的掌握它们。
测试代码:
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.2二叉树的遍历及逻辑操作.php
推荐学习:php视频教程
以上がバイナリツリートラバーサルと論理演算方法の詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

