3 分で木と二分木について学ぶ

コンピュータの分野では、私たちが毎日扱う[フォルダー]やデータベースに保存されるデータはすべてツリーの典型的な応用例です。今日は、ツリーとバイナリ ツリーのより理論的な定義と、それらの属性と特徴の一部について学びます。

ツリー

実際の上記の例から、ツリー構造がその特性の一部を要約できることがわかります。

ツリー (ツリー) は N (N>0) 個のノードの有限集合であり、空のツリー (N=0) または空ではないツリー T のいずれかです。

この定義では、2 つの問題を明確にする必要があります。第一に、ツリーにはノードが必要です。第二に、ノードの数に応じて、空のツリーと空ではないツリーの 2 つのタイプに分類できます。 。ただし、これは最も基本的な定義にすぎず、いくつかの特性があります。

ルートと呼ばれるノードは 1 つだけあります。

つまり、このツリーは、ツリーのルートと同じ特定のノードから拡張する必要があります。そこから外側に枝分かれし始めます。

ルート ノードを除いて、残りのノードは m ( m > 0 ) 個の互いに素な有限集合 T1、T2...、Tm に分割でき、それぞれはそれ自体がツリーであり、サブツリーと呼ばれます。ルート (サブツリー)

この段落は理解しにくいかもしれませんが、実際には、単刀直入に言うと、各ノードは上位ノードを 1 つだけ持ち、複数の上位ノードを持つことはできません。同様に、水平ノード間に接続はできませんが、複数の下位ノードを持つことができます。

ツリーの定義に関しては、以下の図を参照してください。

#上の図は、標準ツリーと非標準ツリーがどのようなものかを単にリストしたものです。このうち

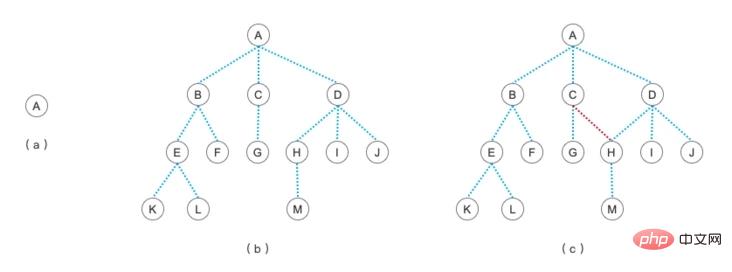
• #(a) はルートノードが 1 つだけの木であり、ノードが 1 つあれば木構造と言えます

• (b) は標準のツリー構造

• (c) です。C ノードと H ノードの間に接続線があることに注意してください。これはツリーではありません。ノード上位ノードを 1 つだけ持つことができるツリーをツリーと呼びます。これは実際に将来学習することになります [図]

#ツリーの関連用語

#スタックのプッシュ (プッシュ) とポップ、キューのエンキューとデキューに比べて、ツリーの関連用語ははるかに複雑です。何はともあれ、最初にこれらの用語を覚えておかなければ、後で説明する内容で使用される用語によってさらに混乱するだけです。しかし、その場では思い出せなくても、最初に大まかな印象を覚えておき、学習の途中で出会ったときにもう一度復習することで、より印象が深くなります。 。

ノード: ノードには、一連のデータ、または他のノードを指す分岐が含まれる場合があり、分岐が分岐する場所とみなすことができます。 、B、C、D、E などはすべてノードの次数です。

• : ノードが所有するサブツリーの数はノードの次数と呼ばれ、実際にはノードの次数です。子ノードの数が次数です。図 (b) では、ノード C の次数は 1、ノード D の次数は 3 です。ツリー: ツリー内の各ノードの次数 ノードの次数の最大値は、最も多くの子ノードを持つ次数であり、これがツリーの次数になります (b) 図のツリーの次数は 3
です

• Leaves: Degree ノードは 0、つまり子ノードのないノード (b) 図中の K、L、F、G、M、I、J は次数の葉ノードです。このツリー

• 親と子: ノードの子ノードはその子であり、これらの子ノードの場合、現在のノードはその親です。 D は H 、 I、 J であり、 H、I、J の親は D

• レベルです。ルート ノードから数えて、ルート ノードが最初のレベルであり、ルート ノードの子は 2 番目のレベルです。など、(b) 図の G ノードのレベルは 3、(a) 図のすべてのレベルは 1

• のみです。ツリーの (高さ): 現在のツリー ツリーの最大レベルは、明らかに、(b) グラフの深さは 4

• 兄弟、先祖、子孫: 兄弟ノードは次のとおりです。これらのノードの親は同じノードです; 祖先ノードはルート ノードから指定されたノードに向かう途中に通過するすべてのノードです; 子孫は特定のノードからターゲット ノードに向かう途中にあるすべてのノードです。 (b) 図では、E と F は兄弟、E の先祖は A と B、E の子孫は K または L

• いとこです。すべて同じレベルにあり、親が異なります。また、図 (b) では、G のいとこは E と F であり、H、I、J もそのいとこです
二分木

• ツリーの概念をある程度理解したら、データ構造とアルゴリズムについてもさらに別の概念を学習します。ツリーの最も重要な形式であるバイナリ ツリーです。

一般に、ツリーの形状は常に変化する可能性があります。たとえば、あるノードには 3 つの子ノードがあり、別のノードには 300 の子ノードがある場合があります。このようなルールのないツリーは実際には操作が非常に面倒ですが、バイナリ ツリーの定義ははるかに単純です。ツリーのプロパティに加えて、もう 1 つのコンテンツもあります。バイナリ ツリーの各ノードには、最大で次の内容があります。 2 つの子ノード。つまり、バイナリ ツリー全体の次数は 2 でなければならず、すべてのノードの次数が 2 を超えることはありません。なぜ二分木が操作しやすいのかについては、次章の二分木の性質で詳しく説明します。すべてのツリー構造は、特定の規則的な変形を通じてバイナリ ツリーに変換できます。

また、図を使用してバイナリ ツリーとは何かを示します。



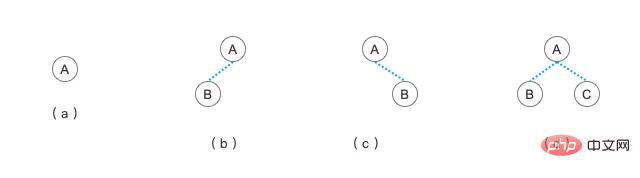
バイナリ ツリーでは、左側の子ノードとその子孫は、現在のノードの左側のサブツリーと見なすことができます。右ノードとその子孫ノードは、現在のノードの右サブツリーとみなすこともできます。ノードの子ノードに応じて、上図に示すようにいくつかの二分木形式が存在します。

• #(a) ツリーはノードが 1 つだけあるツリーであり、ノードが 1 つだけある二分木とも言えます。

• # #(b) ツリーは左ノードが 1 つだけある二分木です

• (c) ツリーは右ノードが 1 つだけある二分木です

• (d ) ツリーは左右 2 つのノードを持つ二分木です

二分木のプロパティ

プロパティ 1 : バイナリ ツリーの i 番目のレベルに最大 2i-1 個のノードがあります (i >= 1)

プロパティ 2: 深さ k のバイナリ ツリーには最大 2k - 1 個のノードがあります (k >= 1)

プロパティ 3: 任意の二分木 T について、終端ノードの数が n0 で、次数 2 のノードの数が n2 の場合、n0 = n2 1

プロパティ 4: n 個のノードを持つ完全なバイナリ ツリーの深さは log2n 1

プロパティ 5: n 個のノードを持つ完全なバイナリ ツリー (その深さは log2n 1) のノードが層順に番号付けされている場合 (最初の層から log2n 1 層まで、各層は左から右へ）、任意のノード i (1

If i = 1 の場合、ノード i はバイナリ ツリーのルートであり、親はありません。i > 1 の場合、その親はノード i / 2
1. 2i > n の場合、ノード i には親がありません。左の子はありません (ノード i はリーフ ノード点です); それ以外の場合、その左の子はノード 2i
2. If 2i 1 > n、ノード i には右の子はありません; それ以外の場合、その右の子はノード 2i です1

二分木の上記 5 つの性質の数学的証明については詳しく説明しませんが、結局のところ、この連載記事の目的は、データ構造とその本質を誰もが学ぶことです。アルゴリズムを単純かつ大雑把に直接使用するのではなく、単純な例を通してアルゴリズムを理解します。証明を導き出すために数式が使用され、その後、画像上で直接計算するだけで済みます。

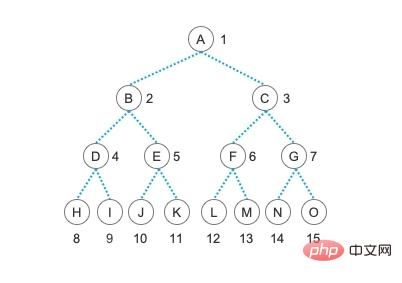
• プロパティ 1 の場合、式によれば、現在のバイナリ ツリーは 3 番目のレベルに最大 23-1 個のノードしか持つことができません。つまり、4 つのノードです。 4 番目のレイヤーには最大でも 24-1、つまり 23 = 8 ノードしか存在できません。

• プロパティ 2 の場合、現在のピクチャのツリーの深さは 4 です。つまり、最大 24 - 1 = 15 個のノードが存在します。

• プロパティ 3 については、まず次数 2 のノードの数を数えます。この図では、次数 2 のノードの数を数えます。 2 7 つの点、つまり A、B、C、D、E、F、G があります。第 4 レベルのノードには子ノードがありません。つまり、それらはすべて 0 度であり、終端ノードとも呼ばれます。ポイント (葉ノード）、これらのノードの数は合計 8 です。ここで、n2 = 7 になります。プロパティの式によれば、n0 = n2 1 = 7 1 = 8

• グラフ内のノードの数は 15 で、プロパティの式を適用すると次のようになります。 log2n 1 = log215 1 = 3.91 (切り捨て) 1 = 3 1 = 4 から 4 を取得できます。現在のツリーの深さは 4 で、プロパティ 4 とプロパティ 2 は相補的なものとみなすことができます。
  プロパティ 5 については、各ノードの端にある番号に注目してください (例として E ノードを選択します)。 E ノードは現在 5 なので、その親は 5 / 2 = 2 (切り捨て) です。E の左の子は 2i (2*5=10)、E の右の子は 2i 1 (つまり 2) です。 *5 1 = 11; プロパティ 5 の定義はより抽象的で、バイナリ ツリー全体を対象とした説明にリーフ ノードを使用していますが、実際には意味はここで説明したものと同じです。他のノードと。プロパティ 5 は、後で説明するバイナリ ツリーを格納するためのシーケンシャル構造の使用にとって非常に重要です。

• バイナリ ツリーのこれら 5 つのプロパティとその意味を必ずマスターして覚えてください。これは、後の学習で、バイナリ ツリーの順序、チェーン ストレージ構造、またはバイナリ ツリーの走査は、上記の 5 つのプロパティの内容にさらされる可能性があります。これらは二分木学習における最も基本的な魂であると言えます。

Forest

最後に、「Forest」とは何かを簡単に理解しましょう。複数の木が集まって「森」を形成します。上の二分木の説明図のように、(a)(b)(c)(d)をまとめて全体として見ると「森」ですが、この「森」の中に(a) (b) (c) (d) これら 4 つの木。

森の中の木の間にはつながりがありません。森を操作したり横断したりする場合、多くの場合、森を木に変換します。特定のアルゴリズムや手順は学習の焦点では​​ないため、誰でも理解できますが、より深く学習したい学生は、関連するコンテンツを検索したり、関連する教科書を参照したりできます。

まとめ

積み木からツリーの後ろに並んでいるとき、突然大きな一歩を踏み出したと感じませんか?少し混乱していますか？関係ありませんが、今日の内容は実際には基礎的な理論的な内容です。理解できる場合は理解して、理解できない場合は勉強を続けてから、今日の概念を見てください。

学習とは、常に進歩のプロセスを繰り返すことではなく、もちろん、すべては基礎に基づいていなければなりません。ツリーのデータ構造と簡単なトラバーサル アルゴリズムを理解したら、もう一度これらの概念を深く理解し、暗記してください。一般面接でのツリーに関する質問は問題外になると思います。一緒に頑張りましょう!

推奨学習: php ビデオ チュートリアル

以上が3 分で木と二分木について学ぶの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。