二分木に似たグラフの幅優先走査とは何ですか?
- 青灯夜游オリジナル
- 2020-08-29 16:44:3222661ブラウズ
グラフの幅優先走査は、二分木のレイヤーごとの走査に似た水平優先走査です。幅優先トラバーサルは、ルート ノードから開始してツリーの幅に沿って検索およびトラバースします。つまり、階層的にトラバースします。各レイヤーは上から下に、各レイヤー内で左から右 (または右) に順番にアクセスされます。左) ノードにアクセスするには、1 つのレベルにアクセスした後、アクセスできるノードがなくなるまで次のレベルに入ります。

1. はじめに
ツリー トラバーサルと同様に、グラフ トラバーサルもグラフ内の特定の点から開始され、次に従ってグラフをトラバースします。特定の方法で、グラフ内のすべての頂点を 1 回だけ訪問します。
しかし、グラフの走査はツリーよりも複雑です。グラフ内の頂点は他の頂点に隣接している可能性があるため、繰り返しの訪問を避けるために、グラフの走査中に訪問した頂点を記録する必要があります。
さまざまな検索パスに応じて、グラフ走査の方法を幅優先検索と深さ優先検索の 2 つのタイプに分けることができます。
2. グラフの基本概念
2.1. 無向グラフと無向グラフ
頂点ペア (u, v) は順序付けされていません、つまり (u, v )と (v, u) は同じ側です。通常は一対の括弧で表されます。
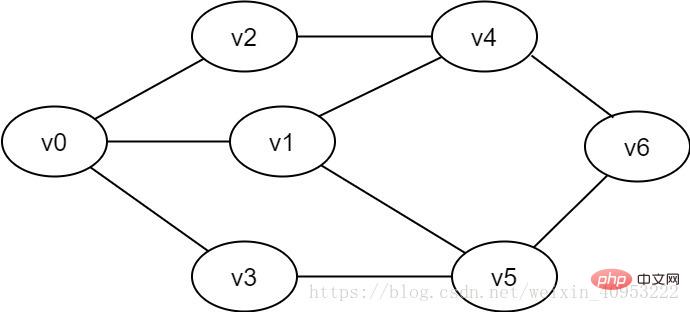
図 2-1-1 無向グラフの例
頂点ペア
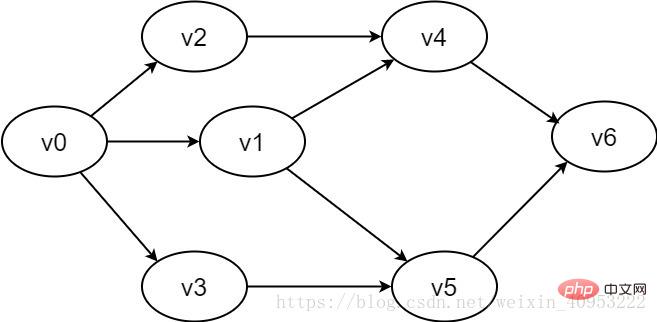
#図 2-1-2 有向グラフの例
##2.2 .Quanhe.net
グラフの各エッジには、エッジの重みと呼ばれる特定の意味を持つ値が含まれる場合があります。この種の重み付きグラフはネットワークと呼ばれます。 2.3. 接続されたグラフと接続されていないグラフ接続されたグラフ: 無向グラフ G では、頂点 v から頂点 v' へのパスがある場合、v と v' が表されます。つながること。グラフ内の任意の 2 つの頂点 v、v'∈V、および v と v' が接続されている場合、G は接続されたグラフであると言われます。上の 2 つのグラフは両方とも接続されたグラフです。 切断グラフ: 無向グラフ G の v と v' の間に切断がある場合、G は切断グラフと言われます。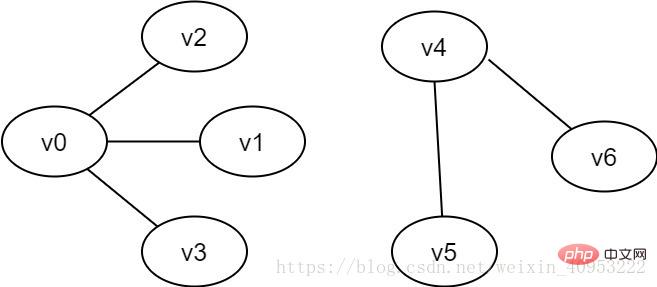
図 2-3 接続されていないグラフの例
3. 幅優先検索
3.1. アルゴリズムの基本的な考え方
幅優先検索は、ツリーの階層横断プロセスに似ています。キューを利用して実装する必要があります。図 2-1-1 に示すように、v0 から v6 までのすべての頂点をトラバースしたい場合は、v0 を最初のレイヤーとして、v1、v2、および v3 を 2 番目のレイヤーとして、v4 と v5 を 3 番目のレイヤーとして設定できます。および v6 4 番目のレイヤーでは、各レイヤーの各頂点が 1 つずつ走査されます。
具体的なプロセスは次のとおりです:
1. 準備: 訪問頂点を記録するために訪問配列を作成します; 各層の頂点を保存するキューを作成します; 初期化 図 G.
2. 図の v0 から訪問を開始し、visited[v0] 配列の値を true に設定し、v0 をキューに追加します。
3. キューが空でない限り、次の操作を繰り返します:
(1) u をチームの先頭にポイントしてキューから抜けます。
(2) u のすべての隣接する頂点 w を順番にチェックし、visited[w] の値が false の場合は、w を訪問し、visited[w] を true に設定して、w をキューに追加します。
3.2. アルゴリズムの実装プロセス
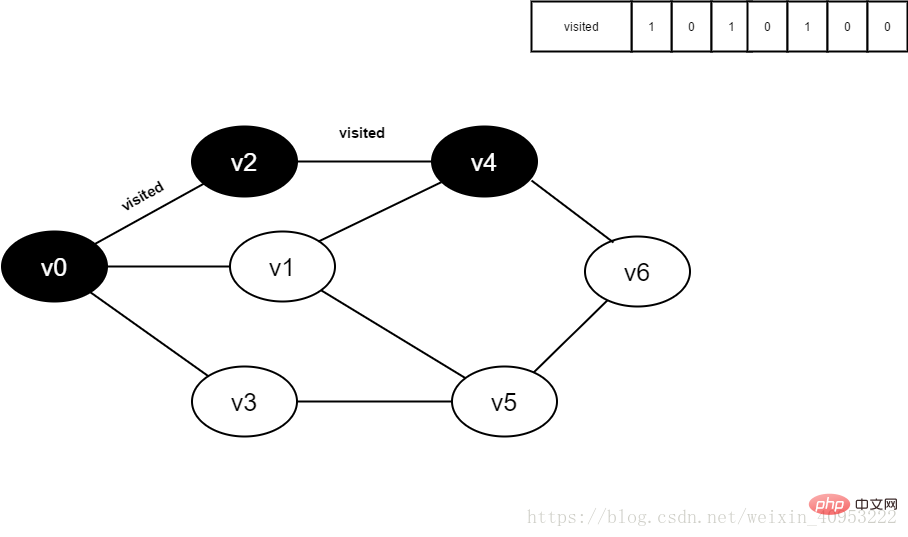
白はまだ訪問されていないことを意味し、灰色はこれから訪問されることを意味し、黒は訪問されたことを意味します。
visited 配列: 0 は訪問されていないことを意味し、1 は訪問されたことを意味します。
キュー: 要素はキューの先頭から出てきて、要素は最後尾から入ります。
1. 最初は、すべての頂点が訪問されておらず、訪問された配列は 0 に初期化され、キューには要素がありません。
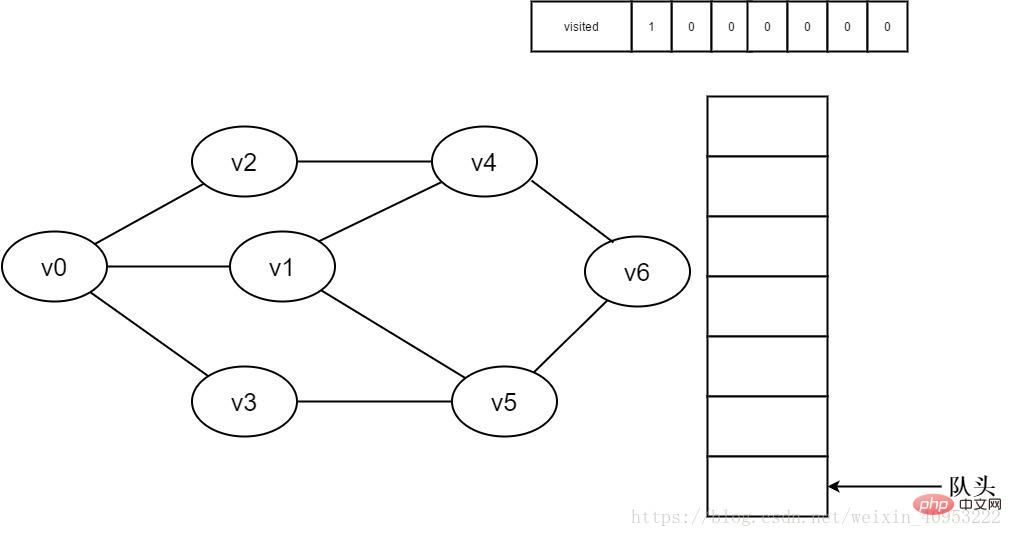
#図 3-2-1
#2. Vertex v0 はまもなくリリースされます。訪問される。
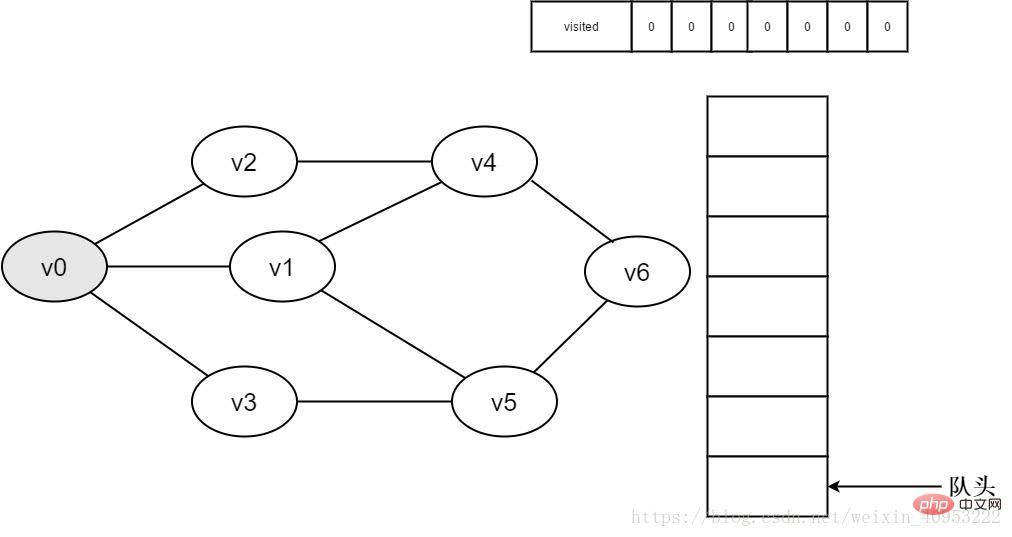
図 3-2-2
3. 頂点 v0 にアクセスし、訪問した場所[0 ]の値は1であり、同時にv0がキューに追加されます。
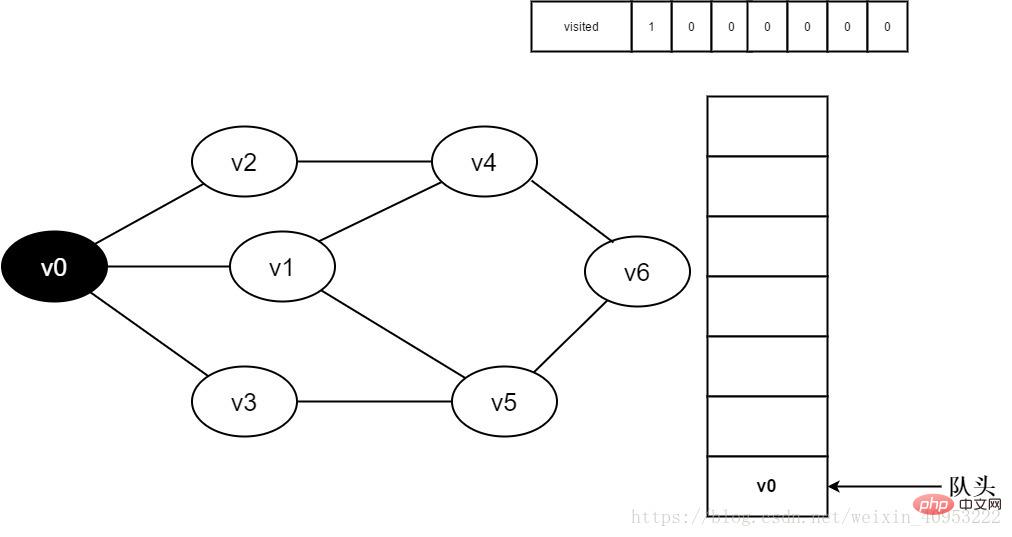
#図 3-2-3
4. v0 をデキューし、v0 の隣接ポイント v2 にアクセスします。 Visited[2] を決定します。visited[2] の値が 0 であるため、v2 を訪問します。
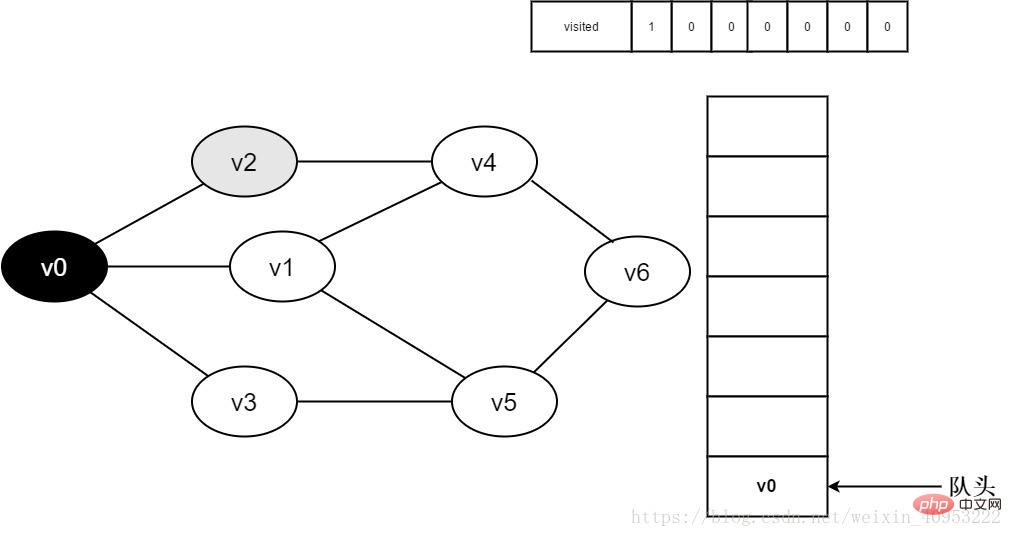
図 3-2-4
5. Visited[2] を 1 に設定し、v2 チームに参加する。
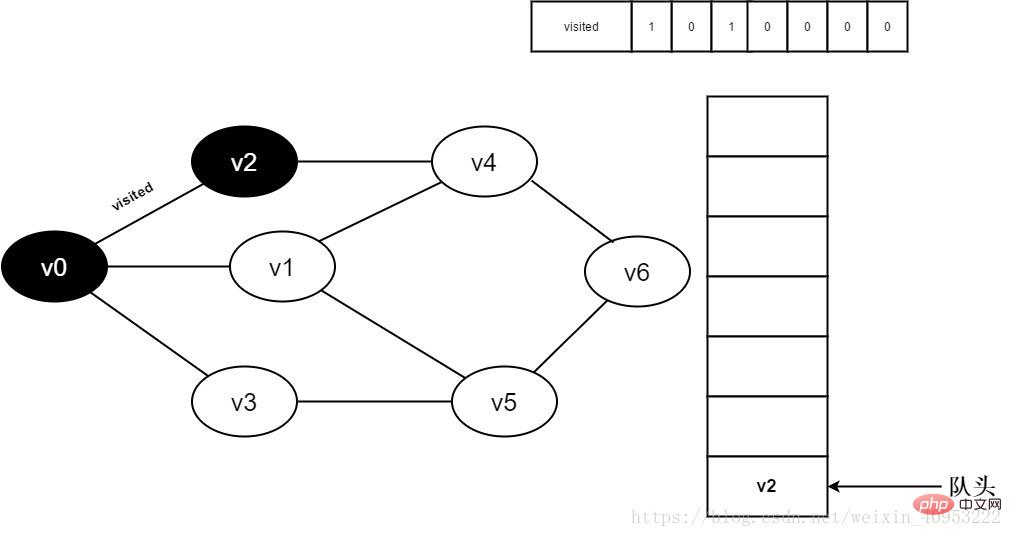
#図 3-2-5
6. v0 隣接ポイント v1 にアクセスします。 Visited[1] を決定します。visit[1] の値が 0 であるため、v1 を訪問します。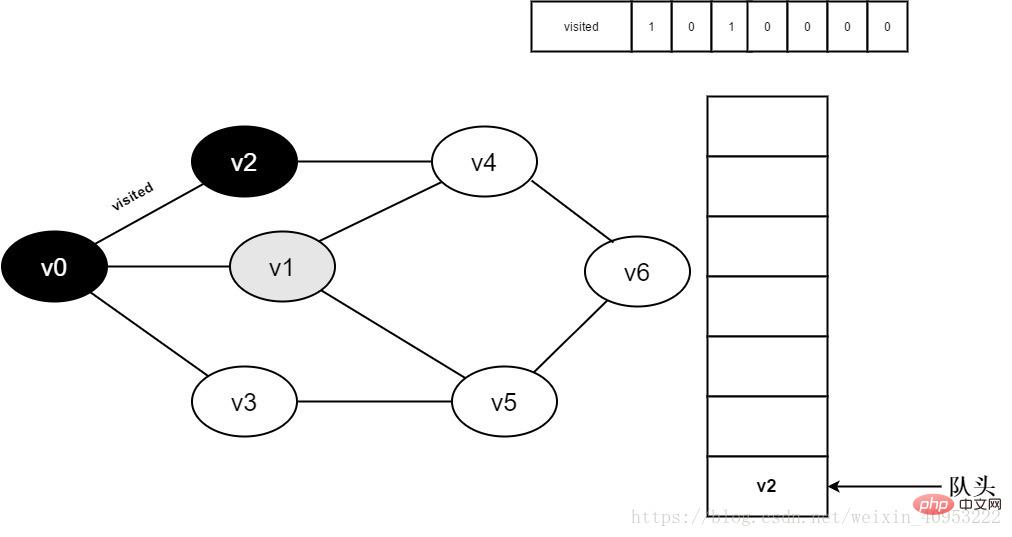
図 3-2-6
7. Visited[1] を 0 および v1 に設定します。 チームに参加する。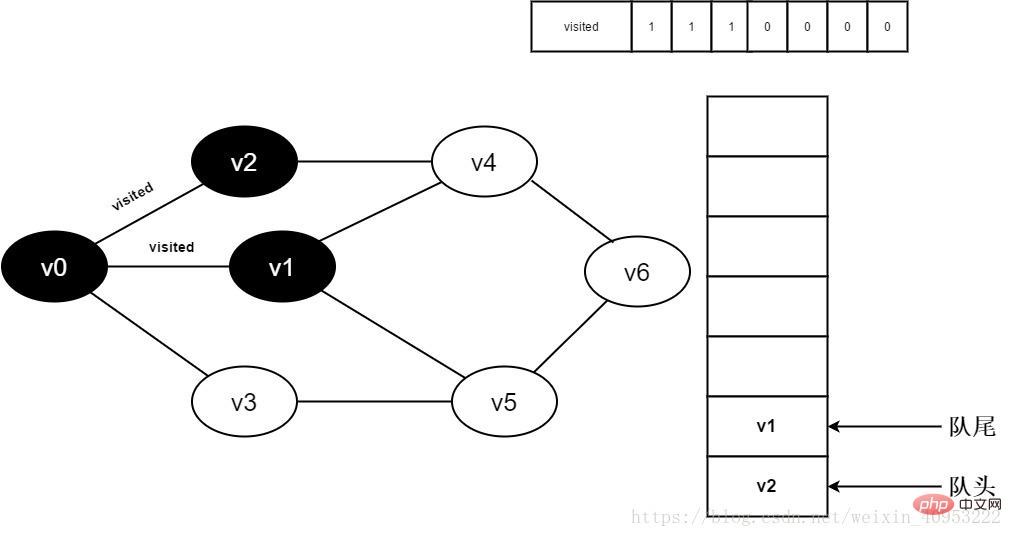
図 3-2-7
8. 裁判官は [3] を訪問しました。値が 0 であるため、アクセスします。 v3. Visited[3] を 0 に設定し、v3 をキューに入れます。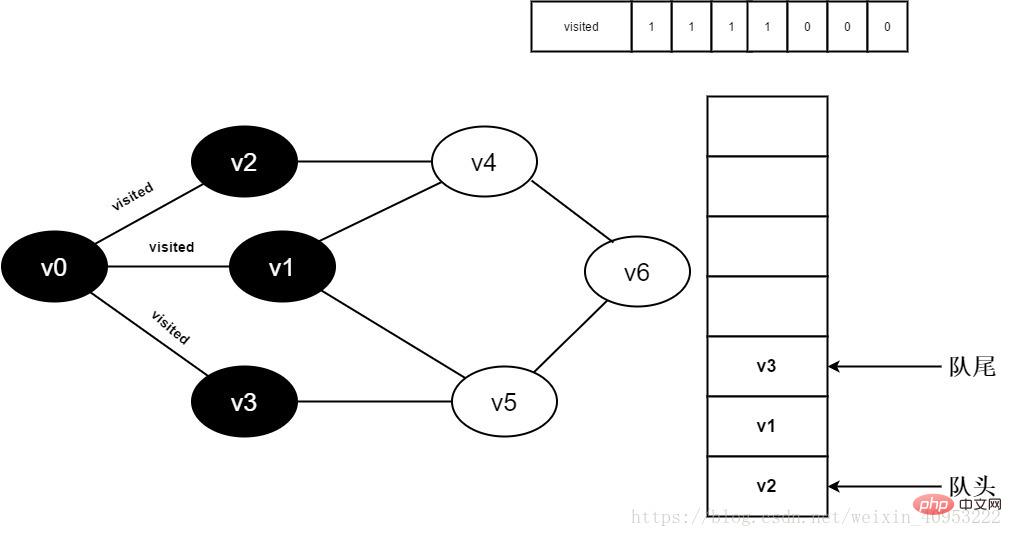
図 3-2-8
9.v0 のすべての隣接ポイントが訪問されました。ヘッド要素 v2 をデキューし、v2 のすべての隣接ポイントへのアクセスを開始します。 v2 隣接点 v0 から訪問を開始し、訪問[0]と判断します。値が 1 であるため、訪問は実行されません。 v2 に隣接するポイント v4 への訪問を続けます。訪問[4]と判断します。その値は 0 であるため、以下に示すように v4 に訪問します。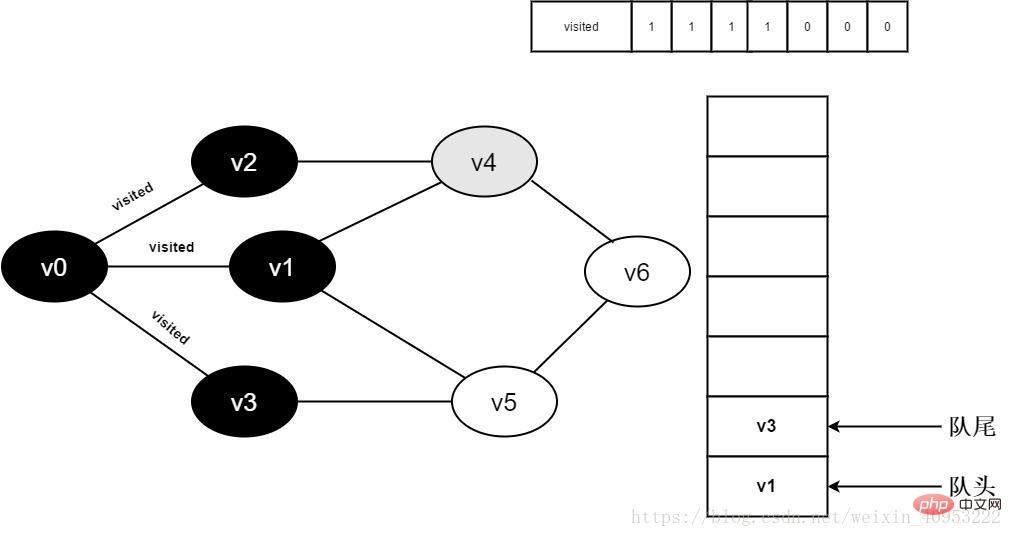
図 3-2-9
10. Visited[4] を 1 に設定し、v4 をキューに追加します。
図 3-2-10
11.v2 のすべての隣接ポイントが訪問されました。ヘッド要素 v1 をデキューし、v1 のすべての隣接ポイントへのアクセスを開始します。 v1 の隣接ポイント v0 への訪問を開始します。visited[0] の値が 1 であるため、訪問は実行されません。 v1 に隣接するポイント v4 への訪問を続けます。visited[4] の値が 1 であるため、訪問は実行されません。 v1 に隣接するポイント v5 への訪問を続けます。visited[5] の値は 0 であるため、以下に示すように v5 にアクセスします。
図 3-2-11
12. Visited[5] を 1 に設定し、v5 をキューに追加します。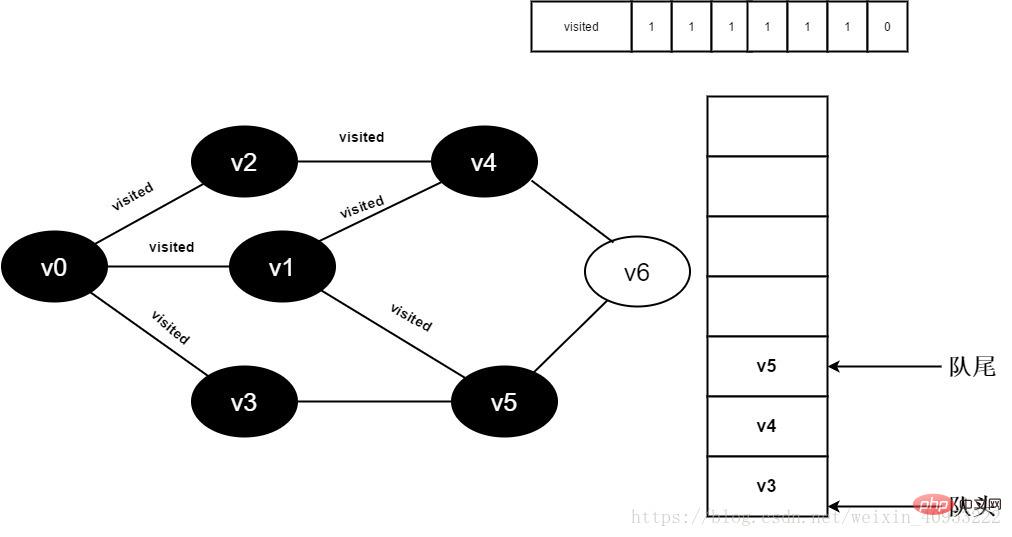
図 3-2-12
13.v1 のすべての隣接ポイントが訪問され、チーム v3 はキューをデキューし、v3 のすべての隣接ポイントへのアクセスを開始します。 v3 隣接ポイント v0 への訪問を開始します。visited[0] 値が 1 であるため、訪問は実行されません。 v3 隣接ポイント v5 への訪問を続けます。visited[5] の値は 1 であるため、訪問は実行されません。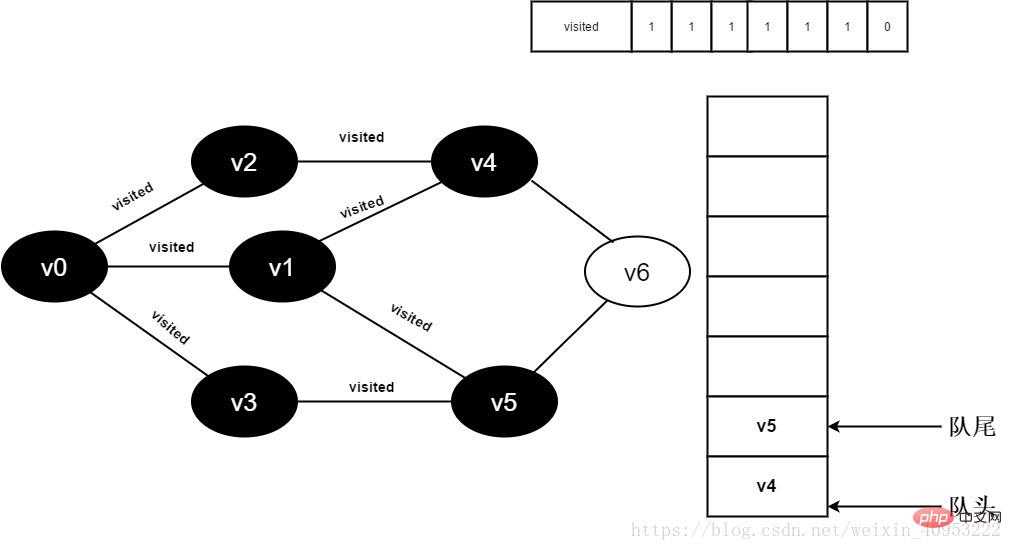
図 3-2-13
14.v3 のすべての隣接ポイントが訪問され、ヘッド要素 v4 がデキューされ、v4 のすべての隣接ポイントへのアクセスが開始されます。 v4 の隣接ポイント v2 の訪問を開始します。visited[2] の値が 1 であるため、訪問は実行されません。 v4 の隣接ポイント v6 への訪問を続けます。visited[6] の値は 0 であるため、以下に示すように v6 にアクセスします。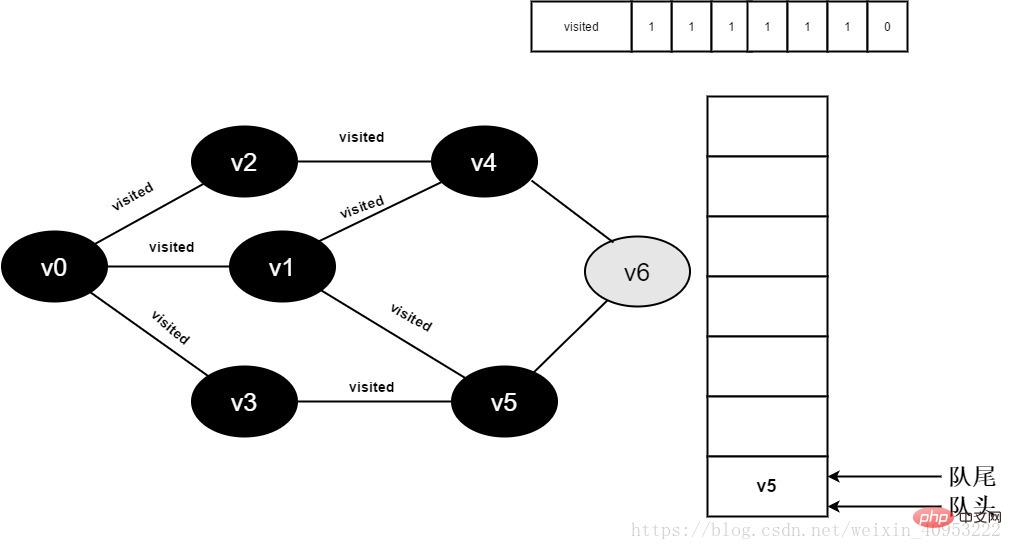
図 3-2-14
15. Visited[6] の値を 1 に設定し、v6 をキューに追加します。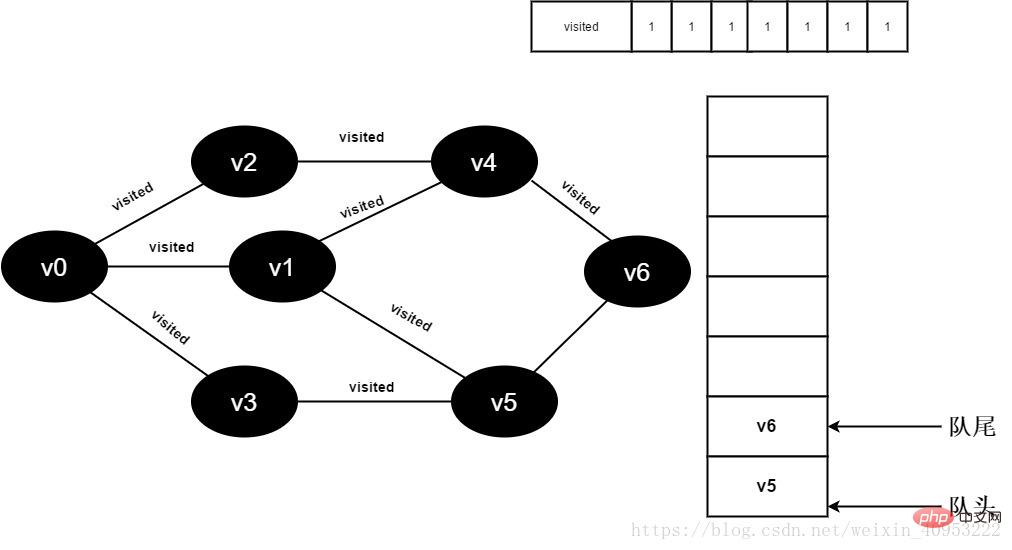
図 3-2-15
16.v4 のすべての隣接ポイントが訪問されました。 v5 がデキューされ、v5 のすべての隣接ポイントへのアクセスが開始されます。 v5 隣接ポイント v3 への訪問を開始します。visited[3] の値が 1 であるため、訪問は実行されません。 v5 隣接ポイント v6 への訪問を続けます。visited[6] の値は 1 であるため、訪問は実行されません。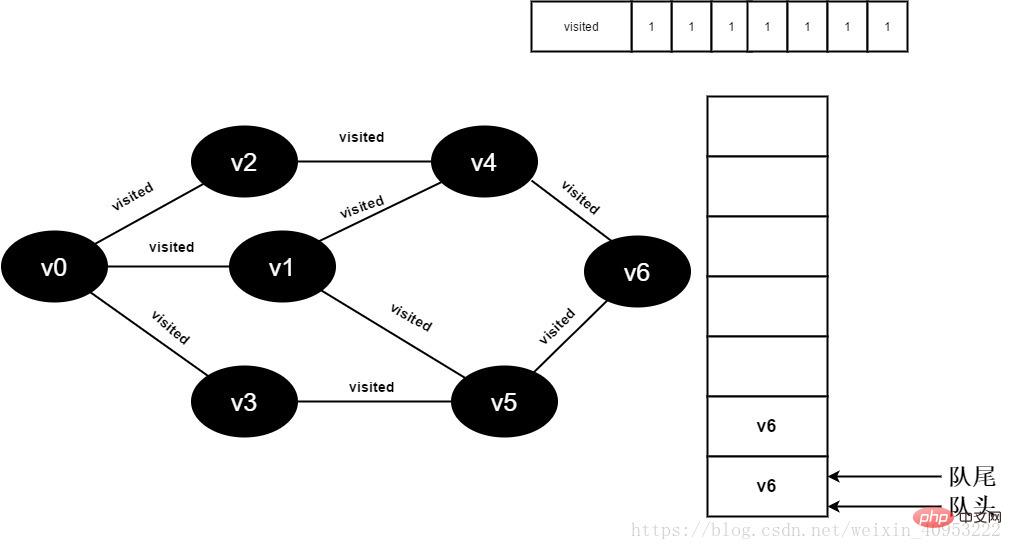
図 3-2-16
17.v5 のすべての隣接ポイントが訪問されました。 v6 がデキューされ、v6 のすべての隣接ポイントへのアクセスが開始されます。 v6 隣接ポイント v4 への訪問を開始します。visited[4] の値が 1 であるため、訪問は実行されません。 v6 隣接ポイント v5 への訪問を続けます。visited[5] の値が 1 であるため、訪問は実行されません。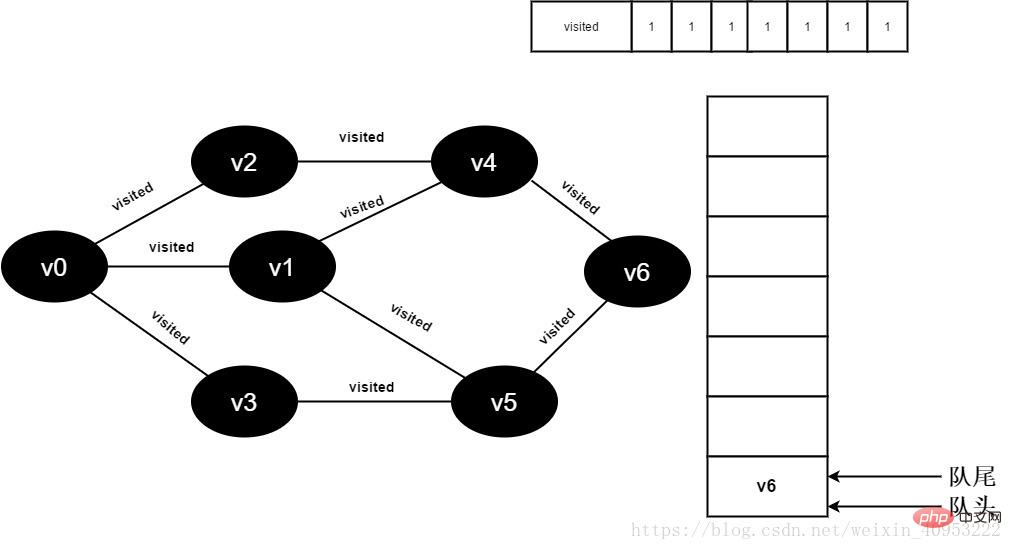
図 3-2-17
18. キューは空です。ループを終了し、すべての頂点が訪問されました。 。
図 3-2-18
3.3 実装の詳細コードの
#3.3.1 隣接行列を使用してグラフの幅優先検索を表現します
/*一些量的定义*/ queue<char> q; //定义一个队列,使用库函数queue #define MVNum 100 //表示最大顶点个数 bool visited[MVNum]; //定义一个visited数组,记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;
/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法,创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar(); //获取'\n’,防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边,0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边,无向图不区分方向
}
return 1;
}/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}3.3.2 隣接リストを使用してグラフの幅優先検索を表現します
/*找到顶点对应的下标*/
int LocateVex(ALGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (v == G.vertices[i].data)
return i;
}/*邻接表存储表示*/
typedef struct ArcNode //边结点
{
int adjvex; //该边所指向的顶点的位置
ArcNode *nextarc; //指向下一条边的指针
int info; //和边相关的信息,如权值
}ArcNode;
typedef struct VexNode //表头结点
{
char data;
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VexNode,AdjList[MVNum]; //AbjList表示一个表头结点表
typedef struct ALGraph
{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;/*采用邻接表表示法,创建无向图G*/
int CreateUDG_2(ALGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar();
for (i = 0; i < G.vexnum; i++) //输入各顶点,构造表头结点表
{
scanf("%c", &G.vertices[i].data); //输入顶点值
G.vertices[i].firstarc = NULL; //初始化每个表头结点的指针域为NULL
}
for (k = 0; k < G.arcnum; k++) //输入各边,构造邻接表
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的两个顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
ArcNode *p1 = new ArcNode; //创建一个边结点*p1
p1->adjvex = j; //其邻接点域为j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; // 将新结点*p插入到顶点v1的边表头部
ArcNode *p2 = new ArcNode; //生成另一个对称的新的表结点*p2
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p1;
}
return 1;
}
/*采用邻接表表示图的广度优先遍历*/
void BFS_AL(ALGraph &G, char v0)
{
int u,w,v;
ArcNode *p;
printf("%c ", v0); //打印顶点v0
v = LocateVex(G, v0); //找到v0对应的下标
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将顶点v0入队
while (!q.empty())
{
u = q.front(); //将顶点元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍历顶点u的邻接点
{
w = p->adjvex;
if (!visited[w]) //顶点p未被访问
{
printf("%c ", G.vertices[w].data); //打印顶点p
visited[w] = 1; //顶点p已被访问
q.push(G.vertices[w].data); //将顶点p入队
}
}
}
}
3.4.接続グラフの幅優先走査の非実装方法
/*广度优先搜索非连通图*/
void BFSTraverse(AMGraph G)
{
int v;
for (v = 0; v < G.vexnum; v++)
visited[v] = 0; //将visited数组初始化
for (v = 0; v < G.vexnum; v++)
if (!visited[v]) BFS_AM(G, G.vexs[v]); //对尚未访问的顶点调用BFS
}4.深さ優先探索
4.1 アルゴリズムの基本的な考え方
深さ優先検索は、ツリーの事前順序走査に似ています。具体的には、プロセスは次のとおりです。
準備: 訪問済みの配列を作成して、訪問済みの頂点をすべて記録します。
1. 図の v0 から始めて、v0 にアクセスします。
2. v0 の最初の未訪問の隣接点を見つけて、頂点を訪問します。この頂点を新しい頂点として使用し、訪問したばかりの頂点に未訪問の隣接頂点がなくなるまでこの手順を繰り返します。
3. 未訪問の隣接点がまだある以前に訪問した頂点に戻り、次の未訪問の頂点の先頭点への訪問を続けます。
4. すべての頂点にアクセスして検索が終了するまで、手順 2 と 3 を繰り返します。
4.2 アルゴリズムの実装プロセス
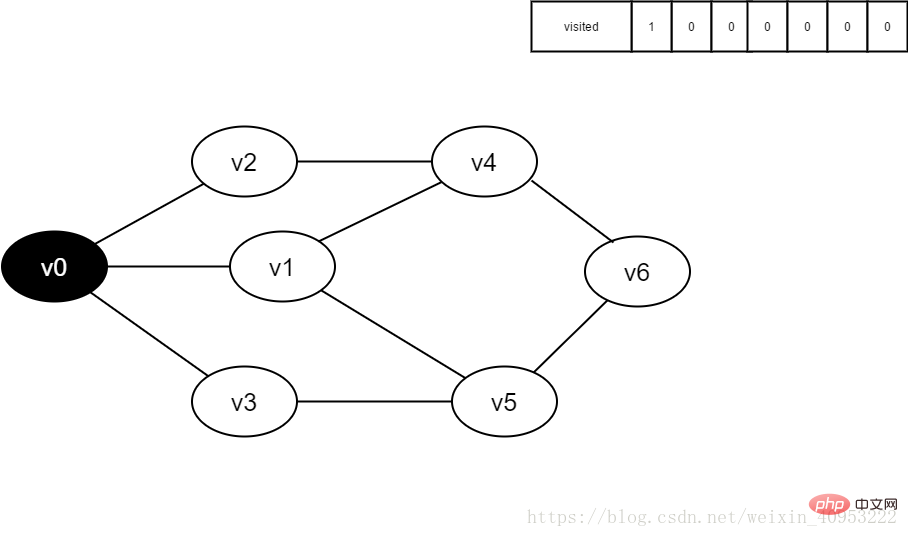
1. 最初は、すべての頂点が訪問されておらず、訪問された配列は空です。

#図 4-2-1

図 4-2-2
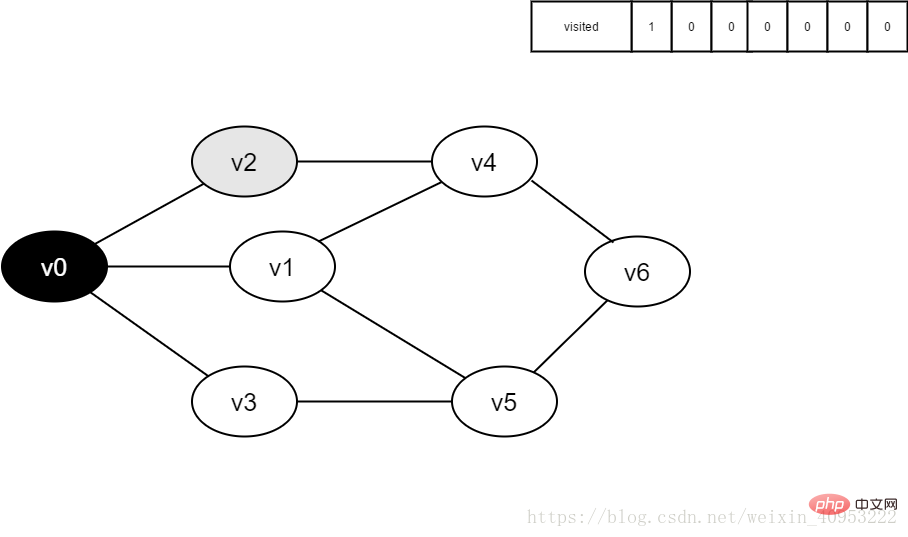
5. Visited[2] を 1 に設定します。
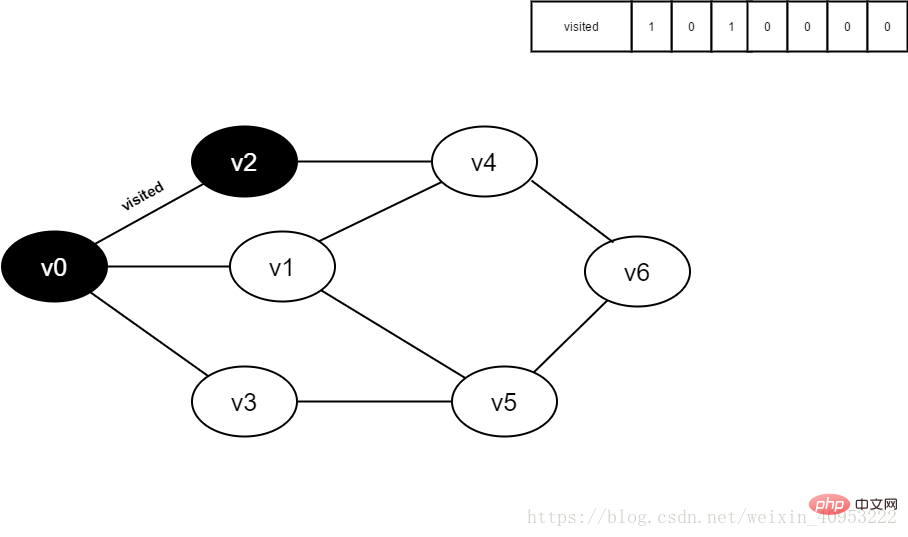
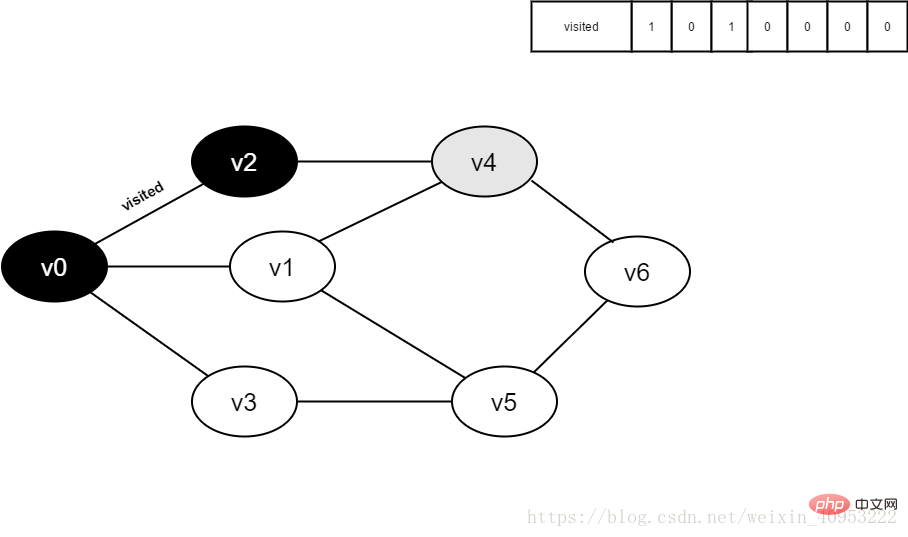
7. Visited[4] を 1 に設定します。
8. v4 の隣接ポイント v1 を訪問し、visited[1] を決定し、その値は 0 で、v1 にアクセスします。
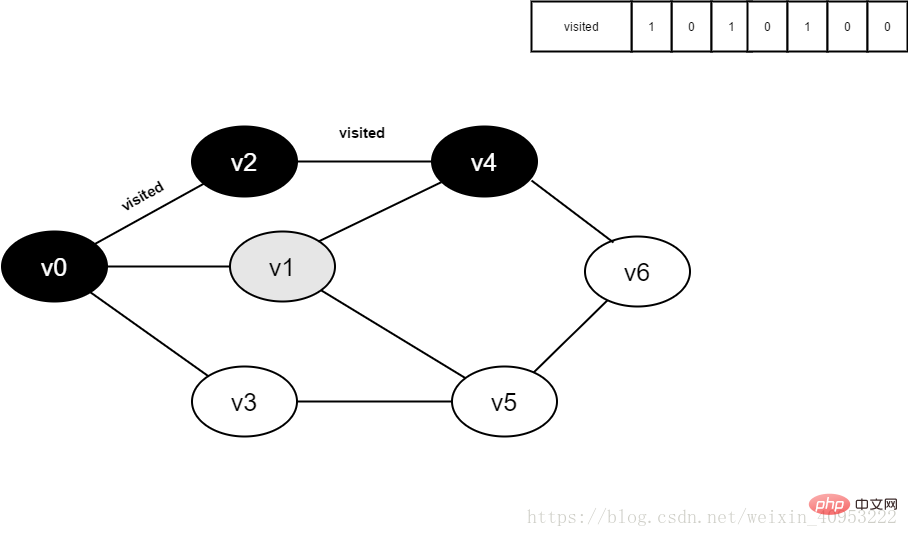
9. Visited[1] を 1 に設定します。
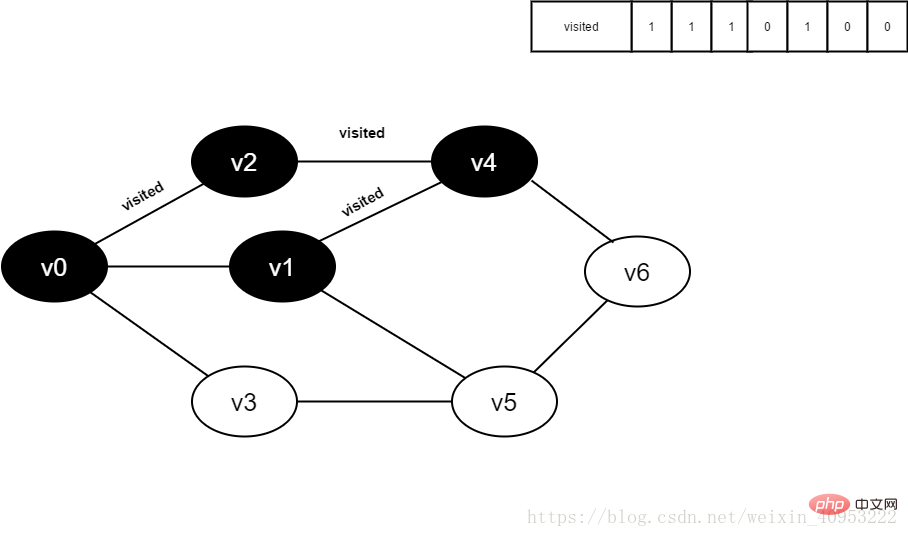
#図 4-2-9
10. v1 の隣接ポイント v0 を訪問し、決定します。値が 1 である Visited [0] はアクセスされません。
v1 の隣接ポイント v4 への訪問を続けます。訪問済み[4]と判断され、その値は 1 であり、訪問しません。
v1 の隣接ポイント v5 への訪問を続け、visited[5] を解釈します。その値は 0 で、v5 を訪問します。
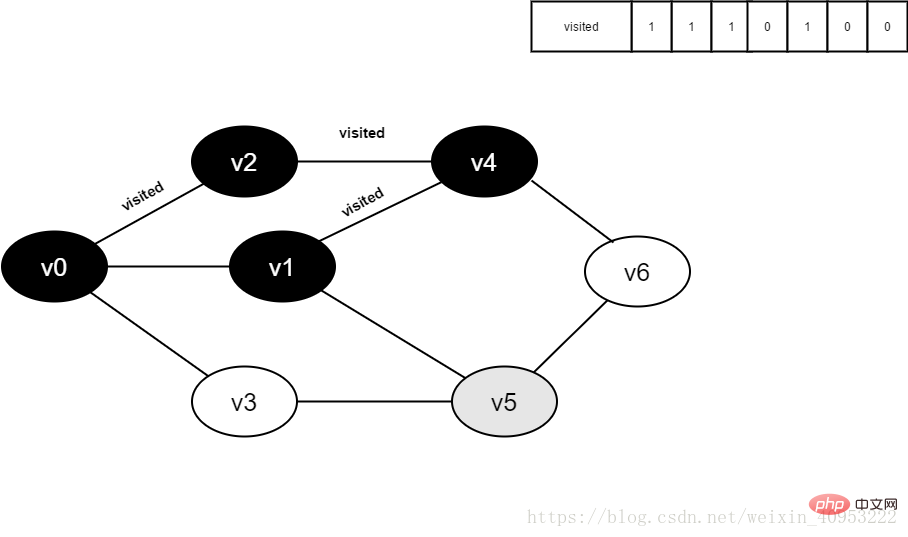
#図 4-2-10
11. Visited[5] を 1 に設定します。
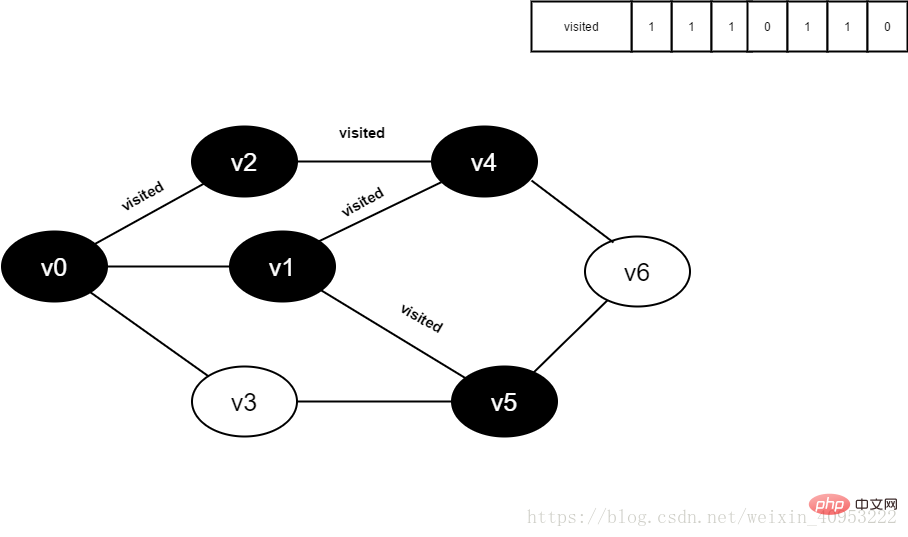
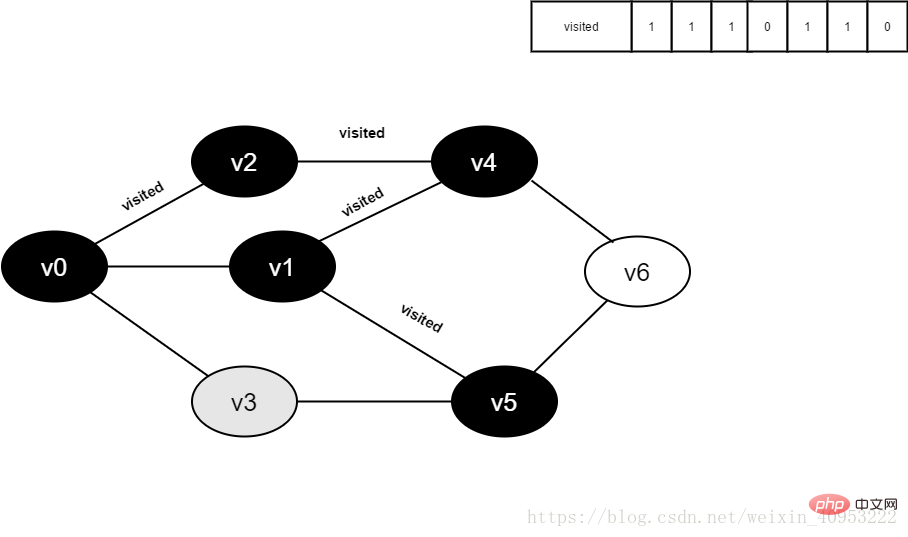
图4-2-12
13.将visited[1]置为1。
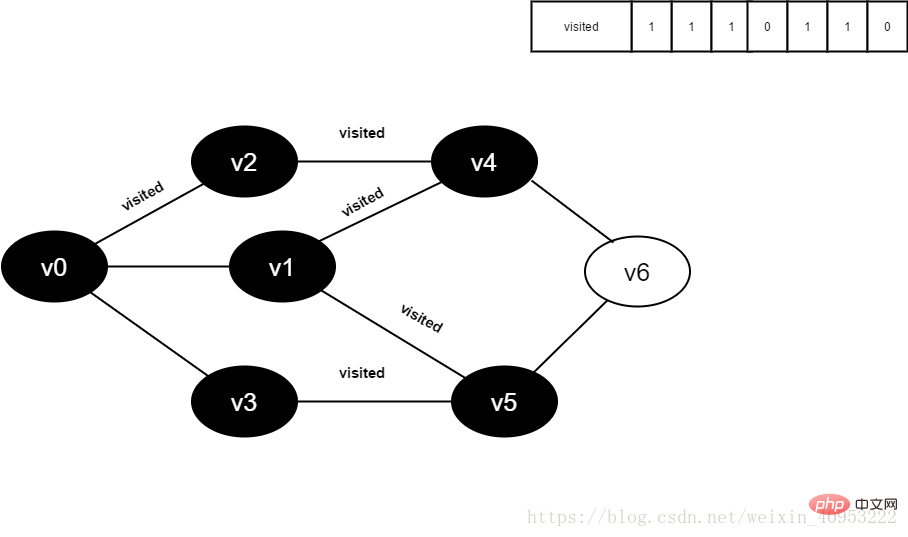
图4-2-13
14.访问v3的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v3的邻接点v5,判断visited[5],其值为1,不访问。
v3所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5所有邻接点。
访问v5的邻接点v6,判断visited[6],其值为0,访问v6。
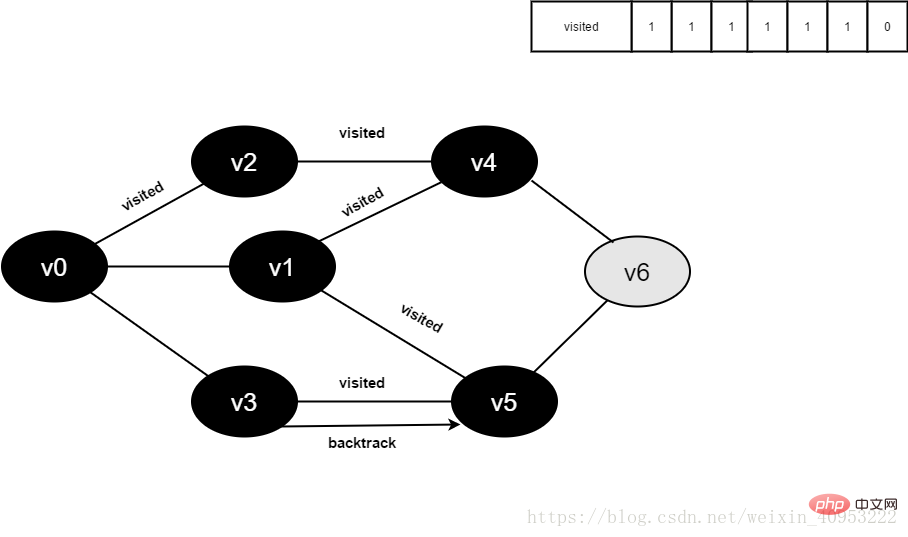
图4-2-14
15.将visited[6]置为1。
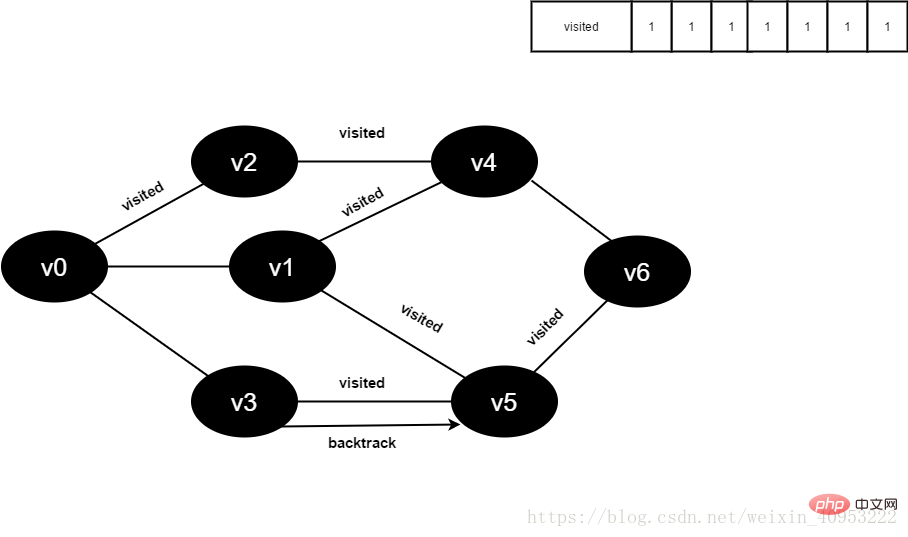
图4-2-15
16.访问v6的邻接点v4,判断visited[4],其值为1,不访问。
访问v6的邻接点v5,判断visited[5],其值为1,不访问。
v6所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5剩余邻接点。
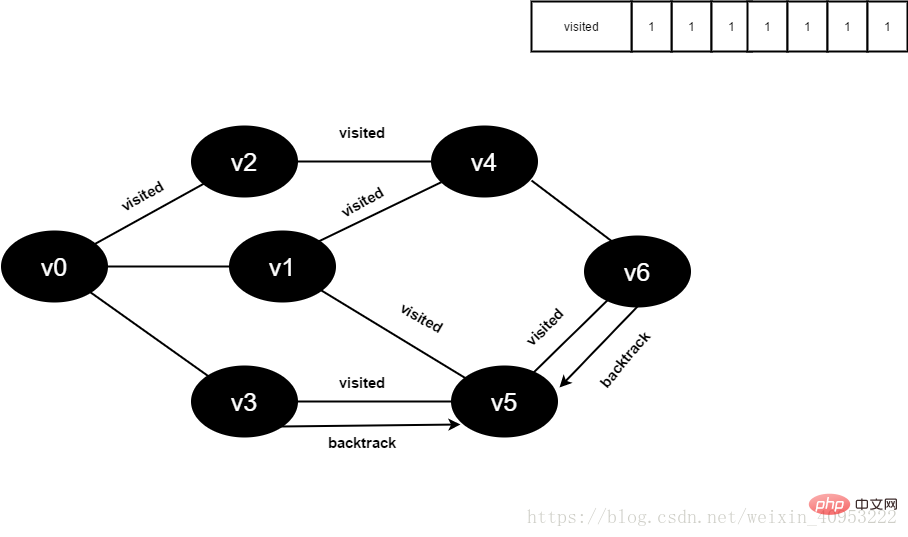
图4-2-16
17.v5所有邻接点均已被访问,回溯到其上一个顶点v1。
v1所有邻接点均已被访问,回溯到其上一个顶点v4,遍历v4剩余邻接点v6。
v4所有邻接点均已被访问,回溯到其上一个顶点v2。
v2所有邻接点均已被访问,回溯到其上一个顶点v1,遍历v1剩余邻接点v3。
v1所有邻接点均已被访问,搜索结束。
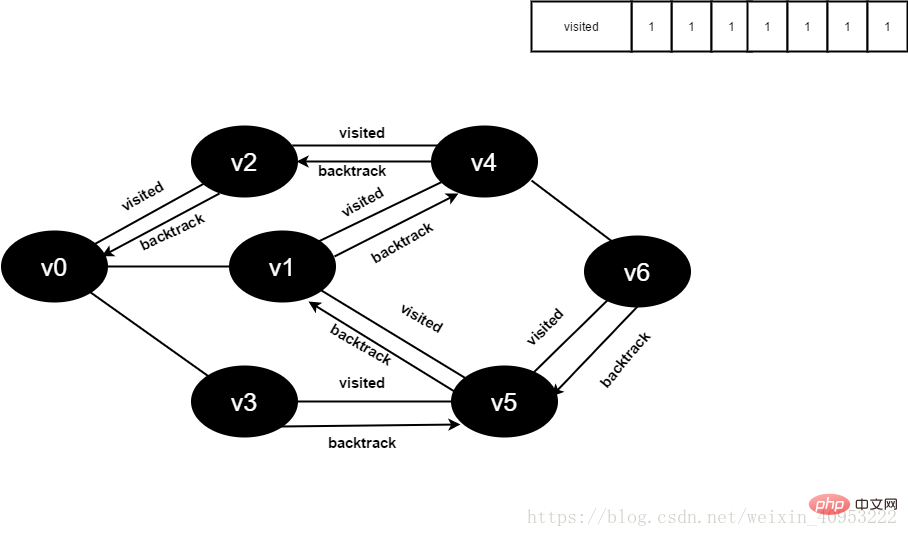
图4-2-17
4.3具体代码实现
4.3.1用邻接矩阵表示图的深度优先搜索
邻接矩阵的创建在上述已描述过,这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}4.3.2用邻接表表示图的深度优先搜素
邻接表的创建在上述已描述过,这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}
更多相关知识,请访问:PHP中文网!
以上が二分木に似たグラフの幅優先走査とは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。