Java におけるバイナリ ツリーの深さ優先トラバースの詳細な説明

過去 2 日間、私は二分木に関連するアルゴリズムの質問をし、勉強ノートをとっていました。 (バイナリ ツリーの作り方さえ知りませんか? あなたは本当に熟練していないので、日常業務でバイナリ ツリーに関連するアルゴリズムやデータ構造を書く必要はありません。私はそれが得意なので、書かなければなりません。もっと勉強してください!)

定義

まず Wikipedia の説明を見てみましょう: コンピュータ サイエンスでは、Binary Tree (英語) : 二分木) は、最大 2 つの分岐を持つノードです (つまり、分岐次数が 2 を超えるノードを持つ木構造は存在しません)。通常、ブランチは「左サブツリー」または「右サブツリー」と呼ばれます。二分木の枝には左と右の順序があり、自由に逆転することはできません。

バイナリ ツリー自体によって定義される特性により、バイナリ ツリーは高度なローカル再現性を備えているため、バイナリ ツリーを深さ優先で走査する場合、通常は再帰的な方法で実装されます。この方法は非常に簡潔で美しく、理解しやすいです。

深さ優先トラバーサル

一般に、バイナリ ツリーの深さ優先トラバーサルには、最も一般的な次の 3 つの順序トラバーサルがあります。ミッドオーダーとポストオーダー。

プレオーダーの走査順序は次のとおりです: ルート ノードにアクセス -> 左のサブツリーを走査 -> 右のサブツリーを走査

中間オーダーの走査順序は次のとおりです:左のサブツリー -> ルート ノードにアクセス -> 右のサブツリーをトラバース

事後探索順序は次のとおりです: 左のサブツリーをトラバース -> 右のサブツリーをトラバース -> ルート ノードにアクセス

注 ここでの左側と右側はノードではなくサブツリー全体です。ツリー全体を走査する必要があるため、各走査はリーフ ノードまでこの順序で実行されます。

たとえば、次のようなバイナリ ツリーがあるとします。

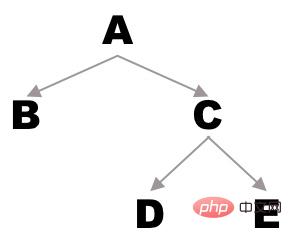
プレオーダー トラバーサルによって得られるシーケンスは、A - B - C - D - E

です。

中次トラバーサルで得られるシーケンスは B - A - D - C - E

ポストオーダー トラバーサルで得られるシーケンスは B - D - E - C - A

We事前順序トラバーサルを使用します (人間の再帰を使用することは強く推奨されません。少なくとも私の脳は 3 つのレベルを処理できません...):

再帰の最初のレベル:

最初にルート ノードにアクセスして、ルート ノードが出力 A になるようにし、次に左側のサブツリー (L1) をトラバースし、次に右側のサブツリー (R1) をトラバースします。

第 2 レベルの再帰:

For L1、ルート ノードが最初にアクセスされるため、この時点での出力はルート ノード B となり、B の左右のサブツリーが空であることがわかり、再帰が終了します。

R1 の場合、最初にルート ノードを作成するため、この時点ではルート ノード C を出力し、次に左側のサブツリー (L2) をトラバースし、次に右側のサブツリー (R2) をトラバースします。

再帰の 3 番目のレベル:

L2 の場合、最初にルート ノードを訪問するため、この時点のルート ノード D が出力され、D の左右のサブツリーが空になり、再帰が終了します;

R2 の場合、最初にルート ノードが訪問されるため、この時点のルート ノード E が出力され、E の左右のサブツリーが空であることがわかり、再帰が終了します。前中後注文の特徴

前中後注文の定義によれば、次のような特徴を見つけるのは難しくありません。 • 事前順序の最初のものはルート ノードである必要があり、事後順序の最後のものはルート ノードである必要があります

• 各種類の左側のサブツリーと右側のサブツリーの分布は規則的です。

• 各サブツリーについて、上記の 2 つのルールに従うツリー

#これらの特性は、定義における順序の表現です。

さまざまな導出

バイナリ ツリー トラバーサルに関する最も基本的なアルゴリズムの質問をいくつか示します。 • バイナリが与えられたとします。ツリー、その前/中/後順序走査のシーケンスを取得します;

• 前順序と中間順序に基づいた後順序の導出 (またはバイナリ ツリー全体の導出);

• 事後順序と順序に基づいて事前順序を推定 (またはバイナリ ツリー全体を推定);

バイナリ ツリーのトラバーサルでは、前述したように、通常は再帰が使用されます。再帰については、直接適用できるテンプレートがあります:

public void recur(int level, int param) {
    
    // terminator
    if (level > MAX_LEVEL) {
        // process result
         return;   
    }
    
    // process current logic
    process(level, param);
    
    // drill down
    recur(level+1, newParam);
    
    // restore current status
}

これは、私が過去 2 日間に視聴したアルゴリズム トレーニング キャンプで、チャオ兄弟 (秦超) が言及した、より実践的なヒントです (このテンプレートは特に上記の 3 つの手順に従ってください (必要なローカル変数がある場合は、手順 4 で解放または追加の処理が行われます)。より順序立てて再帰的なコードを書くことができます。

プレオーダーとミッドオーダーに基づいてポストオーダーを導出する例を次に示します:

最初に 2 つのシーケンスを初期化します:

int[] preSequence = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int[] inSequence = {2, 3, 1, 6, 7, 8, 5, 9, 4};

上記のいくつかの機能を通じて, 最小の繰り返し部分問題が見つかります。各再帰

は、次の

最初のノード値

に従ってノード値が中間に位置するインデックス i と一致します。前のシーケンスを使用して、それぞれ左と右のサブツリーに対応するインデックス i の前部分と後ろ部分を取得し、次に左と右の 2 つのサブツリーをそれぞれ走査して、現在の事前順序の最初のノード値を出力します。ルートノードです。

トップダウン プログラミング手法に従って、最初に次の初期再帰呼び出しを作成できます:

List<Integer> result = new ArrayList<>();
preAndInToPost(0, 0, preSequence.length, preSequence, inSequence, result);

最初のパラメーターは、プレオーダー シーケンスの最初の要素インデックスを表します。

2 番目のパラメータは順序シーケンスの最初の要素のインデックスを表します;

3 番目のパラメータはシーケンスの長さを表します;

第四个参数表示前序序列；

第五个参数表示后序序列；

第六个参数用于保存结果；

先来考虑终止条件是什么，也就是什么时候结束递归，当我们的根结点为空的时候终止，对应这里就是序列长度为零的时候。

if (length == 0) {
    return;
}

接着考虑处理逻辑，也就是找到索引 i：

int i = 0;
while (inSequence[inIndex + i] != preSequence[preIndex]) {
    i++;
}

然后开始向下递归：

preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
result.add(preSequence[preIndex]);

因为推导的是后序序列，所以顺序如上，添加根结点的操作是在最后的。前三个参数如何得出来的呢，我们走一下第一次遍历就可以得出来。

前序序列的第一个结点 1 在中序序列中的索引为 2，此时

左子树的中序系列起始索引为总序列的第 1 个索引，长度为 2；

左子树的前序序列起始索引为总序列的第 2 个索引，长度为 2；

右子树的中序系列起始索引为总序列的第 3 个索引，长度为 length - 3；

右子树的前序序列起始索引为总序列的第 3 个索引，长度为 length - 3；

完整代码如下：

/**
 * 根据前序和中序推导后序
 *
 * @param preIndex    前序索引
 * @param inIndex     中序索引
 * @param length      序列长度
 * @param preSequence 前序序列
 * @param inSequence  中序序列
 * @param result      结果序列
 */
private void preAndInToPost(int preIndex, int inIndex, int length, int[] preSequence, int[] inSequence, List<Integer> result) {
    if (length == 0) {
        return;
    }

    int i = 0;
    while (inSequence[inIndex + i] != preSequence[preIndex]) {
        i++;
    }

    preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
    preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
    result.add(preSequence[preIndex]);
}

参考链接

• 维基百科 - 二叉树（https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91）

推荐教程：《java教程》

以上がJava におけるバイナリ ツリーの深さ優先トラバースの詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。