深さ優先トラバーサルと幅優先トラバーサル
- (*-*)浩オリジナル
- 2019-12-19 09:29:0216133ブラウズ

深さ優先トラバーサル
与えられたグラフ G の初期状態では、すべての頂点が訪問されていないと仮定します。最初の開始点 (ソース ポイント) として G の任意の頂点 v を選択すると、深さ優先トラバーサルは次のように定義できます: 最初に開始点 v を訪問し、それを訪問済みとしてマークします。次に v から開始して、各隣接点を検索します。対W (推奨される学習: Web フロントエンド ビデオ チュートリアル )
これまでに w にアクセスしたことがない場合は、w を新しい開始点として使用して、グラフ内のすべてのパスが見つかるまで深さ優先のトラバースを続けます。ソース点へのパスがある v すべての接続された頂点 (ソース点から到達可能な頂点とも呼ばれます) が訪問されるまで。
この時点でグラフ内にまだ訪問されていない頂点がある場合は、別の未訪問の頂点を新しいソース ポイントとして選択し、グラフ内のすべての頂点が訪問されるまで上記のプロセスを繰り返します。
グラフの深さ優先走査は、ツリーの前順序走査に似ています。採用されている探索方法の特徴は、できるだけ深さ方向から探索することです。この探索方法は深さ優先探索と呼ばれます。したがって、この方法を使用してグラフを走査することは、当然、グラフの深さ優先走査と呼ばれます。
端的に言えば、深さ優先トラバーサルとは、南の壁にぶつからないと壁にぶつからないアルゴリズムで、パスを完了したら、分岐したノードに戻ってトラバースを続けるというものです。
図に示すように:
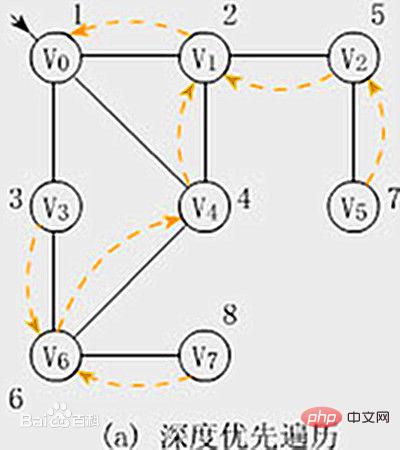
幅優先トラバーサル
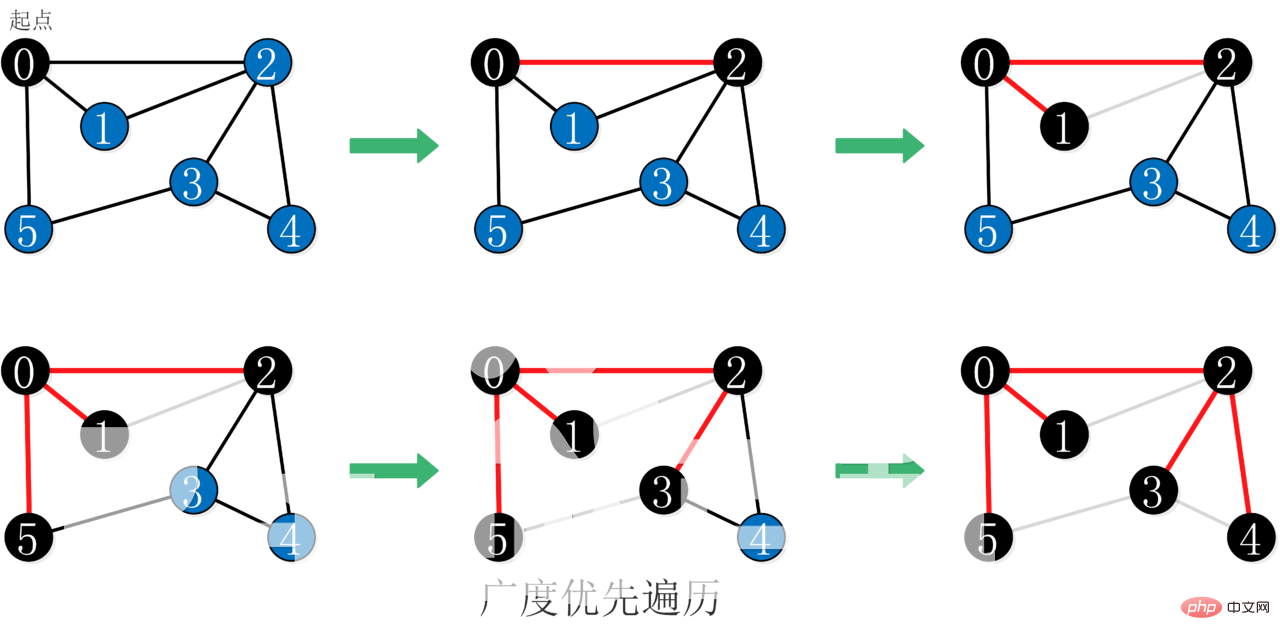
から特定の頂点 V0 から開始してこの頂点を訪問します;
V0 から開始して V0 の各未訪問の隣接点 W1、W2、...、Wk を訪問します;次に、W1、W2、... から開始します。 、Wk のそれぞれを訪問するために訪問されていない隣接点;
すべての頂点が訪問されるまでステップ 2 を繰り返します。
これは、ツリーのレイヤー順序の走査に似た、レイヤーごとのプログレッシブ アルゴリズムです。
幅優先検索中、「レイヤーごと」拡張方法で開始点からトラバースされます。拡張中、ポイントが見つかるたびに、ポイントが全体に到達するまでキューに追加されます。グラフが移動されました。場所。
以上が深さ優先トラバーサルと幅優先トラバーサルの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

