検索

ホームページ >バックエンド開発 >PHPチュートリアル >PHP のバイナリ ツリー深さと幅優先トラバーサル アルゴリズムの手順の詳細な説明

PHP のバイナリ ツリー深さと幅優先トラバーサル アルゴリズムの手順の詳細な説明

php中世界最好的语言
php中世界最好的语言オリジナル
2018-05-16 15:22:312419ブラウズ

今回は、PHP でバイナリ ツリーの深さと幅優先のトラバースを実装するためのアルゴリズムの手順について詳しく説明します。実際のケースを見てみましょう。

序文:

深さ優先トラバーサル

: これ以上深く進めなくなり、各ノードに 1 回しかアクセスできないまで、考えられるすべての分岐パスを深く進みます。バイナリ ツリーの深さ優先トラバーサルは特殊であり、事前順序トラバーサル、順序内トラバーサル、および事後順序トラバーサルに細分できることに注意することが重要です。具体的な手順は次のとおりです。 事前順序トラバーサル: ルート ノード -> 左サブツリー -> 右サブツリー

インオーダー トラバーサル: 左サブツリー -> ルート ノード -> 右サブツリー

事後トラバーサル:左のサブツリー ツリー -> 右のサブツリー -> ルート ノード

幅優先トラバーサル

: 階層トラバーサルとも呼ばれ、各層で左から右に順番にアクセスされます (左から右にアクセスすることもできます)。右から左) に移動してノードにアクセスし、1 つのレベルにアクセスした後、アクセスできるノードがなくなるまで次のレベルに入ります。 たとえば、このツリーの場合:

深さ優先トラバーサル:

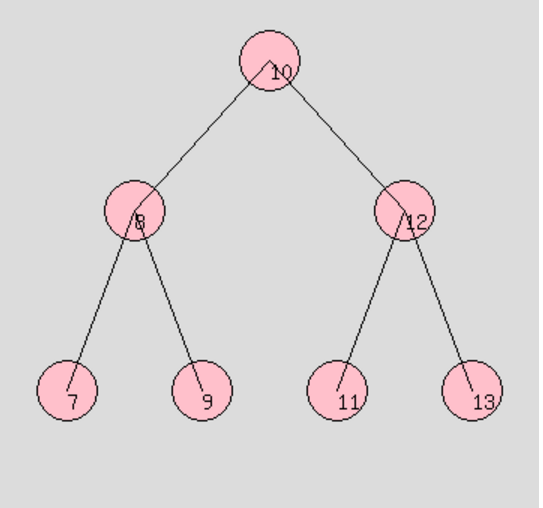
事前順序トラバーサル: 10 8 7 9 12 11 13

順番トラバーサル: 7 8 9 10 11 12 13

投稿する-順序トラバーサル: 7 9 8 11 13 12 10

幅優先トラバーサル:

レベルトラバーサル: 10 8 12 7 9 11 13

バイナリ ツリーの非再帰的深さ優先トラバーサルの一般的な方法は次のとおりです。スタックと非再帰的な幅優先トラバーサルの使用 一般的なアプローチはキューを使用することです。

深さ優先トラバーサル: 1. 事前順序トラバーサル: 

/**
* 前序遍历(递归方法)
*/
private function pre_order1($root)
{
    if (!is_null($root)) {
      //这里用到常量FUNCTION，获取当前函数名，好处是假如修改函数名的时候，里面的实现不用修改
      $function = FUNCTION;
      echo $root->key . " ";
      $this->$function($root->left);
      $this->$function($root->right);
    }
}
/**
* 前序遍历(非递归方法)
* 因为当遍历过根节点之后还要回来，所以必须将其存起来。考虑到后进先出的特点，选用栈存储。
*/
private function pre_order2($root)
{
    //    $stack = new splstack();
    //    $stack->push($root);
    //    while(!$stack->isEmpty()){
    //      $node = $stack->pop();
    //      echo $node->key.' ';
    //      if(!is_null($node->right)){
    //        $stack->push($node->right);
    //      }
    //      if(!is_null($node->left)){
    //        $stack->push($node->left);
    //      }
    //    }
    if (is_null($root)) {
      return;
    }
    $stack = new splstack();
    $node = $root;
    while (!is_null($node) || !$stack->isEmpty()) {
      while (!is_null($node)) {
        //只要结点不为空就应该入栈保存，与其左右结点无关
        $stack->push($node);
        echo $node->key . ' ';
        $node = $node->left;
      }
      $node = $stack->pop();
      $node = $node->right;
    }
}
//前序遍历
public function PreOrder()
{
    // 所在对象中的tree属性保存了一个树的引用
    //   $this->pre_order1($this->tree->root);
    $this->pre_order2($this->tree->root);
}

説明: 1. すべてのトラバーサル メソッドをクラス トラバースにカプセル化しました。 2. pre_order2 メソッドでは、スタックを使用する場合、PHP 標準ライブラリ SPL が提供する splstack を使用します。配列の使用に慣れている場合は、<a href="http://www.php.%20cn/wiki/1001.html" target="_blank">array_push</a>

() および array_pop() シミュレーションの実装。

<a href="http://www.php.cn/wiki/1001.html" target="_blank">array_push</a>() 和array_pop() 模拟实现。

2、中序遍历：

/**
* 中序遍历(递归方法)
*/
private function mid_order1($root)
{
    if (!is_null($root)) {
      $function = FUNCTION;
      $this->$function($root->left);
      echo $root->key . " ";
      $this->$function($root->right);
    }
}
/**
* 中序遍历(非递归方法)
* 因为当遍历过根节点之后还要回来，所以必须将其存起来。考虑到后进先出的特点，选用栈存储。
*/
private function mid_order2($root)
{
    if (is_null($root)) {
      return;
    }
    $stack = new splstack();
    $node = $root;
    while (!is_null($node) || !$stack->isEmpty()) {
      while (!is_null($node)) {
        $stack->push($node);
        $node = $node->left;
      }
      $node = $stack->pop();
      echo $node->key . &#39; &#39;;
      $node = $node->right;
    }
}
//中序遍历
public function MidOrder()
{
    //    $this->mid_order1($this->tree->root);
    $this->mid_order2($this->tree->root);
}

3、后序遍历：

/**
* 后序遍历(递归方法)
*/
private function post_order1($root)
{
    if (!is_null($root)) {
      $function = FUNCTION;
      $this->$function($root->left);
      $this->$function($root->right);
      echo $root->key . " ";
    }
}
/**
* 后序遍历(非递归方法)
* 因为当遍历过根节点之后还要回来，所以必须将其存起来。考虑到后进先出的特点，选用栈存储。
* 由于在访问了左子节点后怎么跳到右子节点是难点，这里使用一个标识lastVisited来标识上一次访问的结点
*/
private function post_order2($root)
{
    if (is_null($root)) {
      return;
    }
    $node = $root;
    $stack = new splstack();
    //保存上一次访问的结点引用
    $lastVisited = NULL;
    $stack->push($node);
    while(!$stack->isEmpty()){
      $node = $stack->top();//获取栈顶元素但不弹出
      if(($node->left == NULL && $node->right == NULL) || ($node->right == NULL && $lastVisited == $node->left) || ($lastVisited == $node->right)){
        echo $node->key.&#39; &#39;;
        $lastVisited = $node;
        $stack->pop();
      }else{
        if($node->right){
          $stack->push($node->right);
        }
        if($node->left){
          $stack->push($node->left);
        }
      }
    }
}
//后序遍历
public function PostOrder()
{
    //    $this->post_order1($this->tree->root);
    $this->post_order2($this->tree->root);
}

广度优先遍历：

1、层次遍历：

/**
* 层次遍历(递归方法)
* 由于是按层逐层遍历，因此传递树的层数
*/
private function level_order1($root,$level){
    if($root == NULL || $level < 1){
      return;
    }
    if($level == 1){
      echo $root->key.&#39; &#39;;
      return;
    }
    if(!is_null($root->left)){
      $this->level_order1($root->left,$level - 1);
    }
    if(!is_null($root->right)){
      $this->level_order1($root->right,$level - 1);
    }
}
/**
* 层次遍历(非递归方法)
* 每一层从左向右输出
元素需要储存有先进先出的特性，所以选用队列存储。
*/
private function level_order2($root){
    if(is_null($root)){
      return;
    }
    $node = $root;
    //利用队列实现
//    $queue = array();
//    array_push($queue,$node);
//
//    while(!is_null($node = array_shift($queue))){
//      echo $node->key.&#39; &#39;;
//      if(!is_null($node->left)){
//        array_push($queue,$node->left);
//      }
//      if(!is_null($node->right)){
//        array_push($queue,$node->right);
//      }
//    }
    $queue = new splqueue();
    $queue->enqueue($node);
    while(!$queue->isEmpty()){
      $node = $queue->dequeue();
      echo $node->key.&#39; &#39;;
      if (!is_null($node->left)) {
        $queue->enqueue($node->left);
      }
      if (!is_null($node->right)) {
        $queue->enqueue($node->right);
      }
    }
}
//层次遍历
public function LevelOrder(){
//    $level = $this->getdepth($this->tree->root);
//    for($i = 1;$i <= $level;$i ++){
//      $this->level_order1($this->tree->root,$i);
//    }
    $this->level_order2($this->tree->root);
}
//获取树的层数
private function getdepth($root){
    if(is_null($root)){
      return 0;
    }
    $left = getdepth($root -> left);
    $right = getdepth($root -> right);
    $depth = ($left > $right ? $left : $right) + 1;
    return $depth;
}

说明：level_order2方法中，在使用队列的过程中，我使用的是PHP标准库SPL提供的splqueue，如果你们习惯使用数组的话，可以使用 array_push() 和array_shift() 模拟实现。

使用：

现在我们来看看客户端代码：

class Client
{
  public static function Main()
  {
    try {
      //实现文件的自动加载
      function autoload($class)
      {
        include strtolower($class) . &#39;.php&#39;;
      }
      spl_autoload_register(&#39;autoload&#39;);
      $arr = array(10, 8, 12, 7, 9, 11, 13);
      $tree = new Bst();
//      $tree = new Avl();
//      $tree = new Rbt();
      $tree->init($arr);
      $traverse = new traverse($tree);
      $traverse->PreOrder();
//      $traverse->MidOrder();
//      $traverse->PostOrder();
//      $traverse->LevelOrder();
    } catch (Exception $e) {
      echo $e->getMessage();
    }
  }
}
CLient::Main();

补充：

1. 在客户端中所使用的三个类 Bst、Avl、Rbt 大家可以参考前面一篇：《PHP实现绘制二叉树图形显示功能详解》

2. 为什么我推荐大家使用SPL标准库中提供的splstack和splqueue呢？这是我在某一篇文章中看到的：虽然我们可以使用传统的变量类型来描述数据结构，例如用数组来描述堆栈（Strack）– 然后使用对应的方式 pop 和 push（array_pop()、array_push()2. インオーダートラバーサル:

rrreee

3. ポストオーダートラバーサル:

rrreee

幅優先トラバーサル: rrreee1. level_order2 メソッド内。 queue を使用するプロセスでは、PHP 標準ライブラリ SPL が提供する splqueue を使用します。配列の使用に慣れている場合は、 array_push() と array_shift() を使用できます。実装をシミュレートします。

使用法:

🎜次に、クライアントコードを見てみましょう: 🎜rrreee🎜🎜🎜補足: 🎜🎜🎜🎜1 クライアントで使用される 3 つのクラス Bst、Avl、および Rbt を参照できます。前回の記事：「PHPでバイナリツリーを描画するグラフィック表示機能を詳しく解説」 🎜🎜2. SPLで提供されているsplstackとsplqueueの使用を推奨する理由標準ライブラリ？これは私が記事で見たものです: スタック (Strack) を記述するために配列を使用するなど、データ構造を記述するために従来の変数型を使用することはできますが、その後、対応するメソッド Pop および Push (array_pop( )) を使用します。 >、array_push()) ですが、注意が必要です。結局のところ、それらはデータ構造を記述するために特別に設計されたものではないため、1 つの間違った操作によってスタックが破壊される可能性があります。 SPL の SplStack オブジェクトは、データをスタックの形式で厳密に記述し、対応するメソッドを提供します。同時に、そのようなコードは、配列ではなくスタック上で動作していることも理解できる必要があり、ピアが対応するコードをよりよく理解できるようになり、処理が高速化されます。元のアドレス: PHP SPL、失われた宝石🎜🎜 この記事の事例を読んだ後は、この方法を習得したと思います。さらに興味深い情報については、PHP 中国語 Web サイトの他の関連記事に注目してください。 🎜🎜推奨読書: 🎜🎜🎜PHPの単純な選択ソートのケースの詳細な説明🎜🎜🎜🎜🎜PHPでハフマンエンコード/デコードを実装する手順の詳細な説明🎜🎜🎜

以上がPHP のバイナリ ツリー深さと幅優先トラバーサル アルゴリズムの手順の詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

声明：
この記事の内容はネチズンが自主的に寄稿したものであり、著作権は原著者に帰属します。このサイトは、それに相当する法的責任を負いません。盗作または侵害の疑いのあるコンテンツを見つけた場合は、admin@php.cn までご連絡ください。
前の記事：PHPバブルソートの使い方を詳しく解説次の記事：PHPバブルソートの使い方を詳しく解説

関連記事

続きを見る