ダイクストラのアルゴリズムを使用してメーデーに向けて最も経済的な旅行ルートを見つける方法

明日はメーデーです。旅行ガイドの準備はできていますか?今回は、ダイクストラ アルゴリズムを使用して、手頃な価格で安心して旅行ルートを簡単に検索できる記事を編集者が紹介します。

ケース:

メーデーがもうすぐ始まり、Xiao Zhang は旅行の準備が整いました。

さまざまな場所の航空券をチェックしました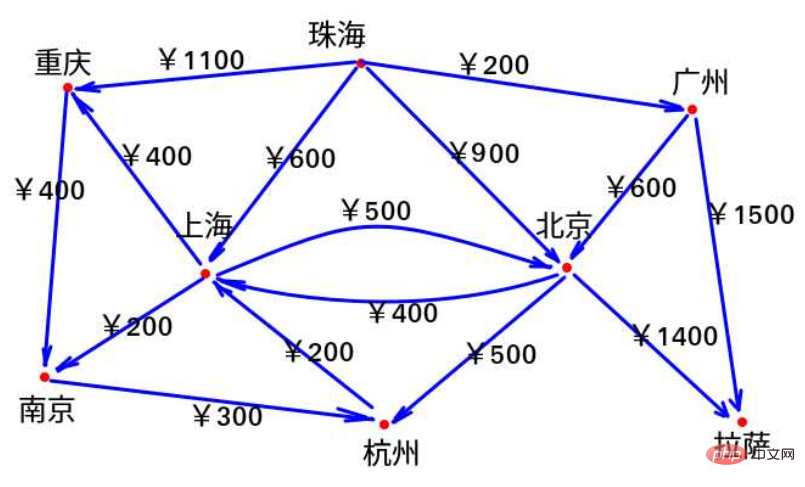


今年は給与が大幅に差し引かれたため、Xiao Zhang さんはあまりお金がなく、気をつけなければなりませんでした。彼の予算。彼はさまざまな都市に行く場合の最安料金を調べたいと考えています。
[まあ、戻ってくるコストを考慮する必要はありません。シャオ・チャンさんは警察の叔父に、自分が人身売買されたので無料で送り返すつもりだった。 】
彼が珠海からラサまで飛行機で行きたい場合、航空券の最低料金はいくらですか?今日説明するアルゴリズムについて話しましょう。

ダイクストラ アルゴリズム

ダイクストラ アルゴリズムは、典型的な単一ソースの最短パス アルゴリズムであり、1 つのノードから他のすべてのノードへの最短パスを計算するために使用されます。最大の特徴は、始点から終点に至るまで、層ごとに外側に広がっていくことです。ダイクストラのアルゴリズムの時間計算量は O(N^2) です。

拡張機能

ダイクストラは、1930 年 5 月 11 日、オランダのロッテルダムの知識人家庭に、4 人兄弟の 3 番目として生まれました。彼の父親は化学者であり発明家であり、オランダ化学会の会長を務めました。彼の母親は数学者です。彼は、障害物のある 2 つの場所間の最短経路を見つけるための効率的なアルゴリズムの設計と実装に成功しました。このアルゴリズムは「ダイクストラのアルゴリズム」と名付けられ、ロボット工学における非常に重要な問題を解決しました。この問題、すなわち動作経路計画問題は、今でも広く使用されています今日。

関連チュートリアル: データ構造アドベンチャー画像の章

アルゴリズム導出

珠海を記録するテーブルの作成各都市への最低航空券費用

珠海から直結している都市を探し始めました

珠海から直結している都市には、上海、北京、広州、重慶、そして珠海から他の都市への航空券の価格は次のとおりです (直接接続がない場合、無限大をマークします):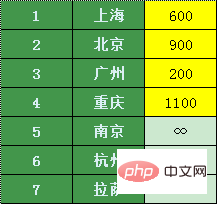

これら 4 つの中で、都市では広州が一番安いので広州から乗り継ぎましょう

広州から一番安い乗り継ぎ方法

##広州から直結できる都市は北京とラサです。珠海から広州から他の都市への乗​​り継ぎ便は以下の通りです。 (広州から乗り継ぎできるかどうかはわかりません)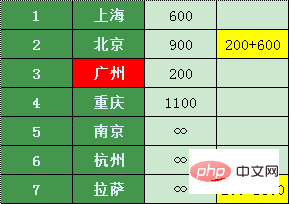

比較したところ、珠海から広州までは200元であることがわかりました。広州から北京までは600元で、たったの800元です（時間のロスかもしれませんが、気にする必要はありません、シャオ・チャンは貧乏で時間しかありません）

広州からラサまでは1700元なので、間違いなく大丈夫ですそこに到着するよりも良いことはありません。
したがって、最安の価格リストがあります。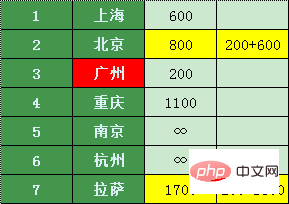

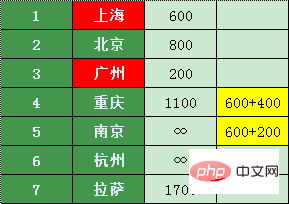
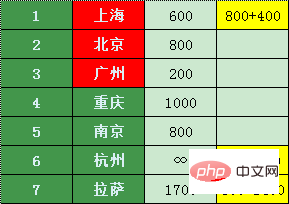
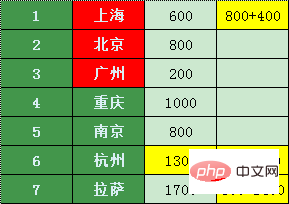
広州に加えて、上海からの乗り換えに最も安い都市を見つけてみましょう - 上海

重慶と南京は上海に直結している都市で、その後珠海に乗り換えることができます。上海から他の都市への航空券の価格は次のとおりです。

元の価格を比較すると、上海から重慶と南京に移動する方が安いことがわかりました

広州と上海を除いて、次に乗り継ぎ便で最も安い都市を探しましょう - 北京

北京から上海への直行便 (上海がマークされています、それが最安のはずです、実際、比較する意味はありません）、杭州とラサの価格は次のとおりです:

ラサまでの価格は北京までの最安値です 800 北京-> の合計ラサ市（2200）の1400の価格は1700より高く、杭州の800の500 = 1300の場合、最低価格リストは次のとおりです。

広州、上海、北京に加えて、乗り継ぎで最も安い都市を探しましょう - 南京

南京から直接行けるのは杭州のみです。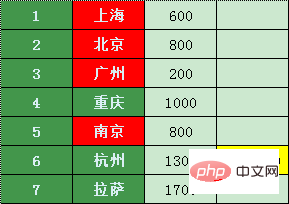

南京からの料金杭州まで 1100 でお得です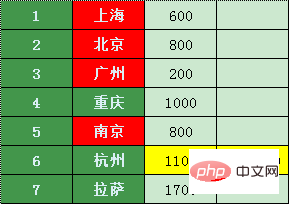

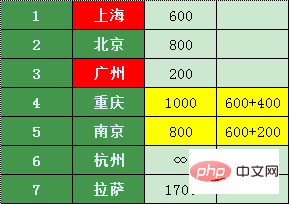
広州、上海、北京、南京に加えて、乗り継ぎ便が最も安い都市を探してみましょう - 重慶

重慶からの唯一の直行便は南京で、南京までは 1000 400 = 1400 元かかります。南京までの当初の 800 元と比較すると、明らかに費用対効果が高くありません。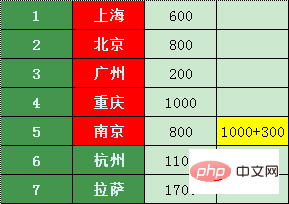

広州、上海、北京、南京、重慶を除いて、私たちからそれから私は最も安い移動ができる都市を探しました - 杭州

杭州は上海までしか行けず、価格は上海より高い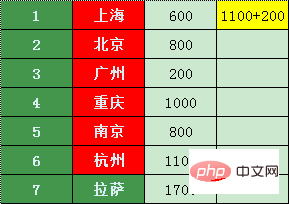

ついにラサを見つけました

すると、ラサまでの最安航空券は1,700元です。

コードの実装

変数の準備

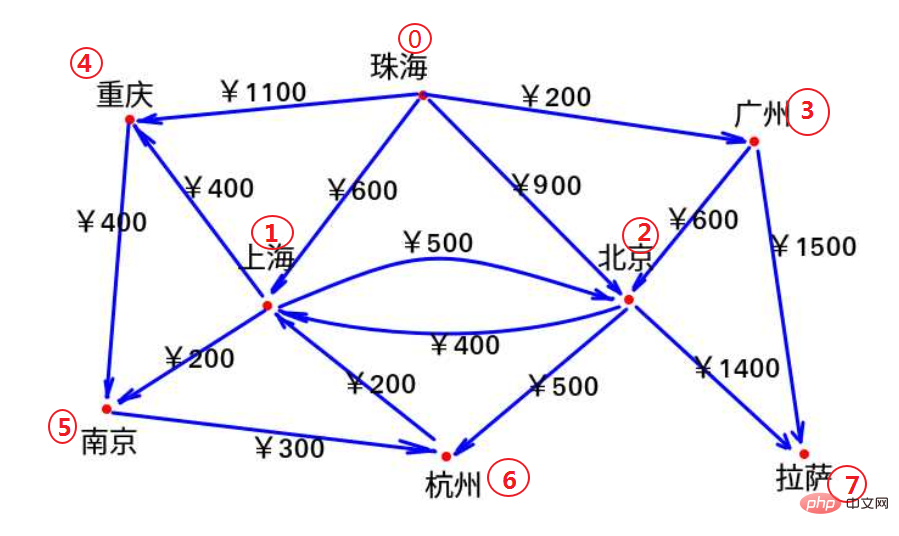
1) 0、1、2、...、7を使用して、珠海、上海、北京、広州、重慶、南京、杭州、ラサ。
2) 航空券の価格を表すには、2 次元配列 価格 [8][8] を使用します。 価格 [i][j] = i から j までの直行便の価格 (航空便がない場合、∞として記録されます) )
3) 配列 minPrice を使用して、珠海からさまざまな都市への航空券の最低コストを記録します。
4) 配列フラグを使用して、都市が転送されたかどうかをマークします。

    //    表示无穷大 即不可达
    public static int NO_AIRPLANE = Integer.MAX_VALUE;
//    初始直飞价格表
    public int[][]  prices ;
    //    最优转机价格表
    public int[]   minPrice ;
    public boolean[] flag ;
    private int citySize;

データ準備

 public static int[][] getPrices(){
        int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS  = 7;
        int[][] prices =  new int[8][8];
        //from Zhuhai
        prices[ZH][CQ] = 1100;
        prices[ZH][SH] = 600;
        prices[ZH][BJ] = 900;
        prices[ZH][GZ] = 200;
        //others
        prices[CQ][NJ] = 400;
        prices[SH][CQ] = 400;
        prices[SH][BJ] = 500;
        prices[SH][NJ] = 200;
        prices[BJ][SH] = 400;
        prices[BJ][HZ] = 500 ;
        prices[BJ][LS] = 1400;
        prices[GZ][BJ] = 600 ;
        prices[GZ][LS] = 1500 ;
        prices[NJ][HZ] = 300 ;
        prices[HZ][SH] = 200 ;
        for(int i = 0 ; i < 8 ; i++){
            for(int j = 0 ; j < 8 ; j++){
                if(prices[i][j] == 0){
                    prices[i][j] =  NO_AIRPLANE;
                }
            }
        }
        return prices;
    }

杭州への直行便を初期化します。価格

//            初始化始发站价格表
        for(int i = 1; i < citySize;i++){
            minPrice[i-1] = prices[0][i];
        }

アルゴリズムの実装

private void dijkstra(){
        int min = Integer.MAX_VALUE;
        int minIdx = Integer.MAX_VALUE;
//        找到最小的价格
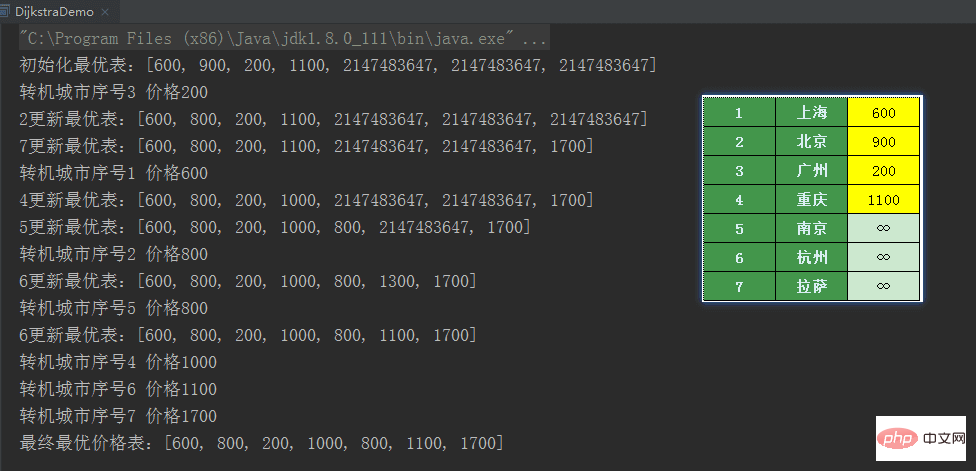
        for(int idx = 0 ; idx 
実行結果

は上記と一致します。プッシュプロセス. この記事があなたのお役に立てば幸いです。 
添付ファイルのソース コード: 
package a;
 
import java.util.Arrays;
 
/**
 * 　　　　　　　　┏┓　　　┏┓+ +
 * 　　　　　　　┏┛┻━━━┛┻┓ + +
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┃　　　━　　　┃ ++ + + +
 * 　　　　　　 ████━████ ┃+
 * 　　　　　　　┃　　　　　　　┃ +
 * 　　　　　　　┃　　　┻　　　┃
 * 　　　　　　　┃　　　　　　　┃ + +
 * 　　　　　　　┗━┓　　　┏━┛
 * 　　　　　　　　　┃　　　┃
 * 　　　　　　　　　┃　　　┃ + + + +
 * 　　　　　　　　　┃　　　┃　　　　Code is far away from bug with the animal protecting
 * 　　　　　　　　　┃　　　┃ + 　　　　神兽保佑,代码无bug
 * 　　　　　　　　　┃　　　┃
 * 　　　　　　　　　┃　　　┃　　+
 * 　　　　　　　　　┃　 　　┗━━━┓ + +
 * 　　　　　　　　　┃ 　　　　　　　┣┓
 * 　　　　　　　　　┃ 　　　　　　　┏┛
 * 　　　　　　　　　┗┓┓┏━┳┓┏┛ + + + +
 * 　　　　　　　　　　┃┫┫　┃┫┫
 * 　　　　　　　　　　┗┻┛　┗┻┛+ + + +
 *
 * @Author:Halburt
 * @Date:2019-04-24 下午 5:47
 * @Description:
 */
public class DijkstraDemo {
 
    //    表示无穷大 即不可达
    public static int NO_AIRPLANE = Integer.MAX_VALUE;
//    初始直飞价格表
    public int[][]  prices ;
    //    最优转机价格表
    public int[]   minPrice ;
    public boolean[] flag ;
    private int citySize;
    /**
     * @param citySize 城市数量
     */
    public DijkstraDemo(int citySize){
        this.citySize = citySize;
//      prices = new int [citySize][citySize];
        flag  =  new boolean [citySize - 1];
        minPrice = new int[citySize - 1 ];
    }
    public static int[][] getPrices(){
        int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS  = 7;
        int[][] prices =  new int[8][8];
        //from Zhuhai
        prices[ZH][CQ] = 1100;
        prices[ZH][SH] = 600;
        prices[ZH][BJ] = 900;
        prices[ZH][GZ] = 200;
        //others
        prices[CQ][NJ] = 400;
        prices[SH][CQ] = 400;
        prices[SH][BJ] = 500;
        prices[SH][NJ] = 200;
        prices[BJ][SH] = 400;
        prices[BJ][HZ] = 500 ;
        prices[BJ][LS] = 1400;
        prices[GZ][BJ] = 600 ;
        prices[GZ][LS] = 1500 ;
        prices[NJ][HZ] = 300 ;
        prices[HZ][SH] = 200 ;
        for(int i = 0 ; i < 8 ; i++){
            for(int j = 0 ; j < 8 ; j++){
                if(prices[i][j] == 0){
                    prices[i][j] =  NO_AIRPLANE;
                }
            }
        }
        return prices;
    }
    public static void main(String[] args) {
        DijkstraDemo demo = new DijkstraDemo(8);
        demo.dijkstra(getPrices());
    }
 
    public void dijkstra(int[][]  prices ){
        this.prices = prices;
//        初始化
//            初始化始发站价格表
        for(int i = 1; i < citySize;i++){
            minPrice[i-1] = prices[0][i];
        }
        System.out.println("初始化最优表：" + Arrays.toString(minPrice));
        dijkstra();
        System.out.println("最终最优价格表：" + Arrays.toString(minPrice));
    }
 
    private void dijkstra(){
        int min = Integer.MAX_VALUE;
        int minIdx = Integer.MAX_VALUE;
//        找到最小的价格
        for(int idx = 0 ; idx < minPrice.length ; idx ++ ) {
            if(!flag[idx] &&  minPrice[idx] < min ){
                min = minPrice[idx];
                minIdx =  idx ;
            }
        }//=已经没有最小的了
        if(minIdx == Integer.MAX_VALUE){
            return ;
        }
        //标记从该城市转机
        flag[minIdx] = true;
        minIdx += 1;
        System.out.println("转机城市序号"+minIdx +" 价格"+ minPrice[minIdx -1]);
       //获取该城市转机时飞往其他城市的价格表
        int cityPrice =  minPrice[minIdx -1];
        //获取杭州飞往该城市的价格
        int[] minCityPrices = prices[minIdx];
        for(int idx = 1 ; idx < citySize ; idx ++ ){
            int price = minCityPrices[idx];
//            如果从杭州到达该城市的价格 加上 idx城市转机的价格 低于  从杭州到达idx城市的价格 则更新
            if(!flag[idx -1 ] && price != NO_AIRPLANE  && (cityPrice+ price) < minPrice[idx - 1]){
//            可达的城市到达的
                minPrice[idx - 1] = cityPrice+ price;
                System.out.println(idx+"更新最优表：" + Arrays.toString(minPrice));
            }
        }
        dijkstra();
    }
 
 
 

 
}
元の著者 Halburt に感謝します。元のアドレス: https://www.cnblogs.com/Halburt/p/10767389.html

以上がダイクストラのアルゴリズムを使用してメーデーに向けて最も経済的な旅行ルートを見つける方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。