C++ を使用して最短パスのダイクストラ アルゴリズムを実装する

ネットワーク層のリンク ステート ルーティング アルゴリズム (LS アルゴリズム)。そのうちの 1 つはダイクストラ アルゴリズムを使用して記述されます。 。 「アルゴリズムの概要」の概要: ダイクストラのアルゴリズムは、重み付き有向グラフ上の単一ソース最短経路問題を解決します。このアルゴリズムでは、すべてのエッジの重みが負でないことが必要です。

アルゴリズムのアイデア

1. G セットはすべての点セットを表し、S セットはソースから点までの最短パスを表します。解決されたある点 点集合、V 集合は最短経路を求めるための点集合として表されます
2. まず S=Ø、V=G

図に示すように、6 つの点と 8 つのエッジがあります V={ 1,2,3,4,5,6}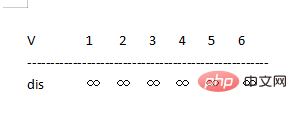

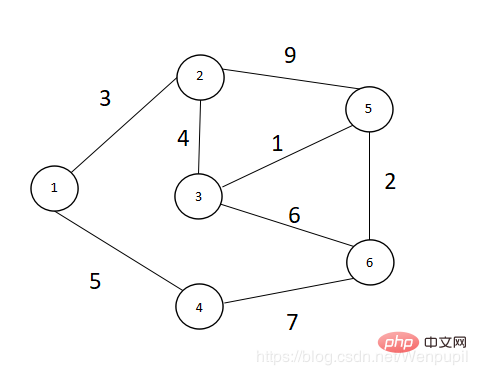
3. u=1 を取り、点 1 を次のように入力します。 S, S={1} ,V ={2,3,4,5,6}、ポイント 1 に接続されているポイントをトラバースし、重みを配列
   
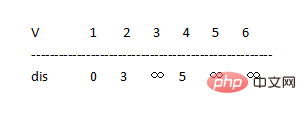
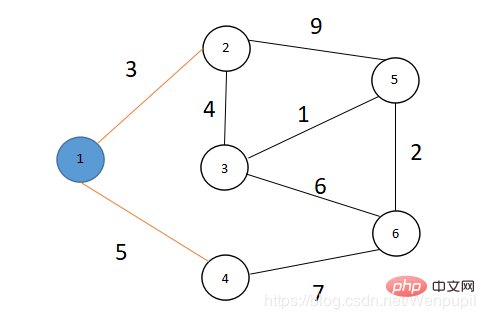# に入れます。

##4. 経路別 配列から、この時点で V 集中点 2 が最短経路 (値は 3) であることがわかるので、u=2、S={1,2}、V とします。 ={3,4,5,6}

なぜなら、 dis[3]=dis[2] 4 ⇒ 7=3 4

… . dis[5]=dis[2] 9 ⇒ 12= 3 9

##同様に、S={1,2},V={3,4,5,6} では、V では次のことがわかります。 [3] は dis[1], dis[2] を除いた最小値なので S=S∪{3}

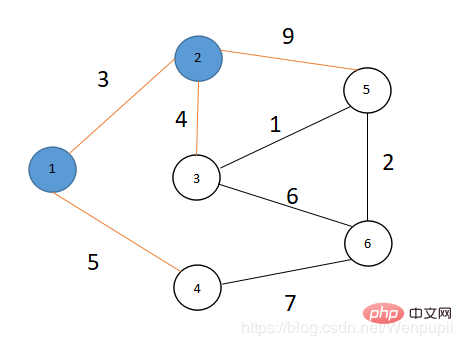
5. このとき S={1,2,3}, V={4 ,5,6}
   
dis[5]=12>dis[3] 1=7 1 ⇒ dis[5]=dis[3] 1=7 1=8 とする

because dis[6]=∞ >dis[3] 6= 7 6 ⇒ dis[6]=dis[6] 6=7 6=13

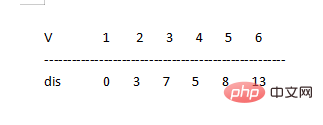とします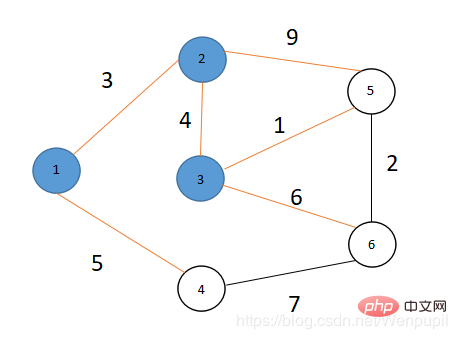#同様に、S={1,2,3}、V={4,5,6} では、V では dis[4] が dis[1]、dis[2 を除く最小値であることがわかります。 ], dis[3] なので、S=S∪{4}

このとき S={1,2,3,4},V={5,6}
6. 
   ##dis[6]=13>dis[4] 7 =5 7 ⇒ dis[6]=dis[4] 7=5 7=12

なので
同様に、S={1,2,3, 4}, V={5,6} では、V では dis[5] が dis[1], dis[ を除く最小値であることがわかります。 2], dis[3], dis[4] なので、S=S ∪{5}

このとき S={1,2,3,4,5},V={6} となります。

7. 
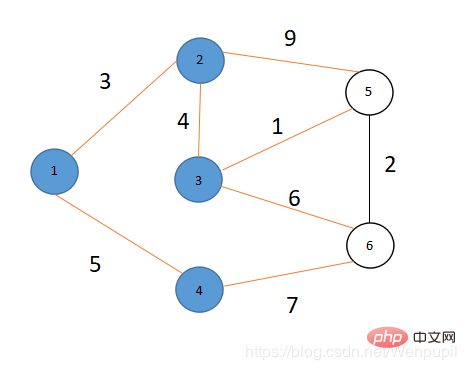
   # because dis[6]=12> ;dis[5] 2=8 2 ⇒ dis[6]=dis[5] 2=8 2=10## とします

#地点 1 から上記の各地点までの最短経路 経路を把握するだけ 最近の文章は非常に乱雑でわかりにくいように感じます。でも、ここまで見てくださった皆様、ありがとうございました。

n 個の点と m 個のエッジの最短経路を見つけるには、通常、n 回繰り返すことですべての点の最短経路を取得できます。
コードを投稿する時期です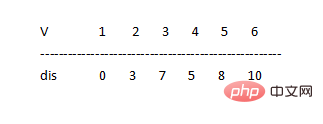

/*
 * @author Wenpupil
 * @time  2019-04-04
 * @version 1.0
 * @Description 最短路径之Dijkstra算法 关于无负权的无向图练习 
 */
#include<iostream>
#include<cmath>
#include<string.h>
#define INIT  9999
using namespace std;
int map[20][20];              //存储19个点的无向图
int s[20];                    //标记数组 
int dis[20];

void mDijkstra(int i,int m)
{
	for(int i=0;i0){
				dis[j]=min(dis[j],dis[u]+map[u][j]);
			}
		}
	}
}

int main(void)
{
	int m,n;                     //共有m个点，n条边
	cin>>m>>n;
	for(int i=0;i<n int cin>>x>>y>>z;
		map[x][y]=map[y][x]=z;
	}
	mDijkstra(1,m);             //从节点1出发 遍历全图
	
	for(int i=1;i<img src="https://img.php.cn/upload/article/000/000/031/6c4fc49b63a8f81ba859050c3ce9aa22-11.png" alt="C++ を使用して最短パスのダイクストラ アルゴリズムを実装する"><p><br><br></p>
<link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-258a4616f7.css" rel="stylesheet">## [推奨コース: <!-- flowchart 箭头图标 勿删 --><svg xmlns="http://www.w3.org/2000/svg" style="display: none;"> # C ビデオ チュートリアル <path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path></svg>#]<h2><span style="font-size: 16px;"></span></h2></n></string.h></cmath></iostream>

以上がC++ を使用して最短パスのダイクストラ アルゴリズムを実装するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。