JS でソートおよび検索アルゴリズムを実装する方法

この記事の内容は、JS を使用してソートと検索のアルゴリズムを実装する方法を紹介するものであり、一定の参考価値があります。必要な友人は参照してください。お役に立てば幸いです。

1. 準備

本題に入る前に、いくつかの基本的な関数を準備します

(1) 配列の 2 つの要素を交換します

function swap(arr, sourceIndex, targetIndex) {
  let temp = arr[sourceIndex];
  arr[sourceIndex] = arr[targetIndex];
  arr[targetIndex] = temp;
}

(2) 0~N

function createArr(length) {
  return Array.from({length}, (_, i) => i);
}

(3) シャッフル関数

シャッフル機能は、配列をすぐに混乱させる可能性があります。一般的な用途には、音楽の再生順序の切り替えが含まれます

function shuffle(arr) {
  for (let i = 0; i <h2><strong>2。並べ替え</strong></h2><p>一般的な並べ替えアルゴリズム</p>

• 比較ソート: 時間計算量が O(nlogn) を超えることができないため、比較を通じて要素間の相対的な順序を決定します。 、そのため、非線形時間比較ソートとも呼ばれます
• 非比較ソート: 比較によって要素間の相対的な順序を決定するのではなく、時間の下限を突破することができます。比較ベースの並べ替え は線形時間で実行されるため、線形時間非比較並べ替えとも呼ばれます

この記事では、次の並べ替え方法はいくつかしかありません。比較ソート 学習の概要

2.1 バブル ソート

バブル ソートはすべてのソート アルゴリズムの中で最も単純であり、通常はソートを学習するための入門的な方法です。ただし、実行時間の観点から見ると、バブル ソートは最悪のソート方法です。

コア: 隣接する 2 つの項目を比較し、最初の項目が 2 番目の項目より大きい場合は、それらを交換します。あたかも泡が表面に浮かび上がっているかのように、アイテムが正しい順序に上に移動されるため、バブル ソートという名前が付けられています。

#Gif:

注: 最初のレベルは、残りの要素の最大値を見つけるためにトラバースし、指定された位置に到達します [最大値が順番にバブルアウトされます]

コード:

function bubbleSort(arr) {
  const len = arr.length;
  for (let i = 0; i  arr[j + 1]) { // 比较相邻元素
        swap(arr, j, j + 1);
      }
    }
  }
  return arr;
}

2.2 選択ソート

選択ソートは、インプレース比較並べ替えアルゴリズムです。

コア: まず、ソートされていないシーケンス内の最小の要素を見つけて、それをソートされたシーケンスの開始位置に格納します。次に、引き続き残りのソートされていない要素から最小の要素を見つけて、それをソートされたシーケンスの終わり。すべての要素がソートされるまで続きます。

Gif:

注: 最初のレイヤーの走査により、残りの要素の最小値のインデックスを取得し、現在位置と最小インデックス値を交換します [最小値を順番に見つけます]

コード:

function selectionSort(arr) {
  const len = arr.length;
  let minIndex;
  for (let i = 0; i  arr[j]) {
        minIndex = j; // 寻找最小值对应的索引
      }
    }
    if (minIndex === i) continue;
    swap(arr, minIndex, i);
  }
  return arr;
}

2.3 挿入ソート

挿入ソートの比較順序はバブルソートや選択ソートとは異なり、現在の項目の前方比較となります。

コア: 順序付けられたシーケンスを構築することにより、並べ替えられていないデータの場合、並べ替えられたシーケンス内で後ろから前にスキャンし、対応する位置を見つけて

GIF を挿入します。 :

注: 現在の項目の前のシーケンスが正しい順序であることを確認するために、2 番目の項目から開始して前方比較します。

コード:

function insertionSort(arr) {
  const len = arr.length;
  let current, pointer;
  for (let i = 1; i = 0 && current <h3>2.4 マージソート<strong></strong>
</h3> 上記の 3 つのソート アルゴリズムと比較すると、マージ ソートとクイック ソートは次のようになります。実際には、より実用的な方が実現可能です (4 番目のセクションでは、実際の複雑さを通じてこれらの並べ替えアルゴリズムを比較します) <p></p><blockquote>JavaScript<code> の </code>Array<code> クラスは # を定義します。 #sort</code> 関数 (<code>Array.prototype.sort</code>) は、<code>JavaScript</code> 配列をソートするために使用されます。 <code>ECMAScript</code> では、使用される並べ替えアルゴリズムが定義されていないため、ブラウザの製造元が独自にアルゴリズムを実装できます。たとえば、<code>Mozilla Firefox</code> は <code>Array.prototype.sort</code> の実装として <strong>mergesort</strong> を使用しますが、<code>Chrome</code> は <code>quicksort バリエーションを使用します。 </code><strong></strong>
</blockquote> マージ ソートは <p>分割統治アルゴリズム<strong>です。このアイデアは、各小さな配列の位置が 1 つだけになるまで元の配列を小さな配列に分割し、並べ替えられた大きな配列が 1 つだけになるまで小さな配列を大きな配列にマージすることです。したがって、<code>recursion</code><code></code></strong>##Core: merge sort、左右の配列に分割、別々に並べ替えてからmerge</p><p>##を使用する必要があります。 <strong>#GIF:</strong></p><p style="text-align: left;"><strong></strong></p><p><strong>注意：递归中最小的左右数组比较为单个元素的数组，因此在较上层多个元素对比时，左右两个数组一定是顺序的</strong></p><p><strong>代码：</strong></p><pre class="brush:php;toolbar:false">function mergeSort(arr) {
  const len = arr.length;

  if (len  right[0]) {
      ret.push(right.shift());
    } else {
      ret.push(left.shift());
    }
  }

  while (left.length) {
    ret.push(left.shift());
  }
  while (right.length) {
    ret.push(right.shift());
  }

  return ret;
}

2.5 快速排序

快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn)，且它的性能通常比其他的复 杂度为O(nlogn)的排序算法要好。和归并排序一样，快速排序也使用分治的方法，将原始数组分为较小的数组

核心：分治算法，以参考值为界限，将比它小的和大的值拆开

动图：

注意：每一次遍历筛选出比基准点小的值

代码：

function quickSort(arr, left = 0, right = arr.length - 1) {
  // left和right默认为数组首尾
  if (left <h2><strong>三、搜索算法</strong></h2><h3><strong>3.1 顺序搜索</strong></h3><p>顺序或线性搜索是最基本的搜索算法。它的机制是，将每一个数据结构中的元素和我们要找的元素做比较。<strong>顺序搜索是最低效的一种搜索算法。</strong></p><pre class="brush:php;toolbar:false">function findItem(item, arr) {
  for (let i = 0; i <h3><strong>3.2 二分搜索</strong></h3><p>二分搜索要求被搜索的数据结构已排序。以下是该算法遵循的步骤：</p><ol>
<li>选择数组的中间值</li>
<li>如果选中值是待搜索值，那么算法执行完毕</li>
<li>如果待搜索值比选中值要小，则返回步骤1在选中值左边的子数组中寻找</li>
<li>如果待搜索值比选中值要大，则返回步骤1在选中值右边的子数组中寻找</li>
</ol><pre class="brush:php;toolbar:false">function binarySearch(item, arr) {
  arr = quickSort(arr); // 排序

  let low = 0;
  let high = arr.length - 1;
  let mid;

  while (low  item) {
      high = mid - 1;
    } else {
      return mid;
    }
  }
  return -1;
}

四、算法复杂度

4.1 理解大O表示法

大O表示法用于描述算法的性能和复杂程度。分析算法时，时常遇到一下几类函数

（1）O(1)

function increment(num){
    return ++num;
}

执行时间和参数无关。因此说，上述函数的复杂度是O(1)(常数)

（2）O(n)

以顺序搜索函数为例，查找元素需要遍历整个数组，直到找到该元素停止。函数执行的总开销取决于数组元素的个数(数组大小)，而且也和搜索的值有关。但是函数复杂度取决于最坏的情况：如果数组大小是10，开销就是10；如果数组大小是1000，开销就是1000。这种函数的时间复杂度是O(n)，n是(输入)数组的大小

（3）O(n2)

以冒泡排序为例，在未优化的情况下，每次排序均需进行n*n次执行。时间复杂度为O(n2)

时间复杂度O(n)的代码只有一层循环，而O(n2)的代码有双层嵌套循环。如 果算法有三层遍历数组的嵌套循环，它的时间复杂度很可能就是O(n3)

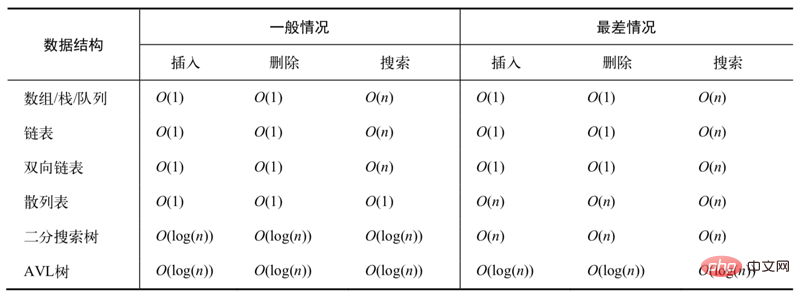
4.2 时间复杂度比较

（1）常用数据结构时间复杂度

（2）排序算法时间复杂度

相关视频教程推荐：《JavaScript教程》

以上就是本篇文章的全部内容，希望能对大家的学习有所帮助。更多精彩内容大家可以关注php中文网相关教程栏目！！！

以上がJS でソートおよび検索アルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。