ホームページ > 記事 > バックエンド開発 > PHPヒープソートの詳しい説明

PHPヒープソートの詳しい説明

小云云オリジナル: 2018-03-29 11:35:261934ブラウズ

ヒープソートとは、積み重ねられたツリー (ヒープ) のデータ構造を使用して設計されたソートアルゴリズムを指し、選択ソートの一種です。配列の特性を利用して、指定したインデックスにある要素をすばやく見つけることができます。ヒープは、大きなルートヒープと小さなルートヒープに分割され、完全なバイナリツリーになります。大規模なルートヒープの要件は、各ノードの値がその親ノードの値以下であること、つまり A[PARENT[i]] >= A[i] であることです。配列の非降順ソートでは、大きなルートヒープの要件に従って、最大値がヒープの先頭になければならないため、大きなルートヒープを使用する必要があります。

ヒープの定義

完全なバイナリツリーにおいて、親ノードが常に子ノード以上 (以下) である場合、それはビッグトップヒープ (スモールトップヒープ) です。

ヒープ配列の保存方法

完全なバイナリツリーはシーケンシャルストレージに適しているため、配列は完全なバイナリツリーとみなすことができます。

ノードの番号付け: ツリーのルートから始まり、上位レベルから下位レベル、各レベルで左から右に順番にすべてのノードに番号を付けて、バイナリツリー構造全体を反映する線形シーケンスを取得します。

PHPヒープソートの詳しい説明

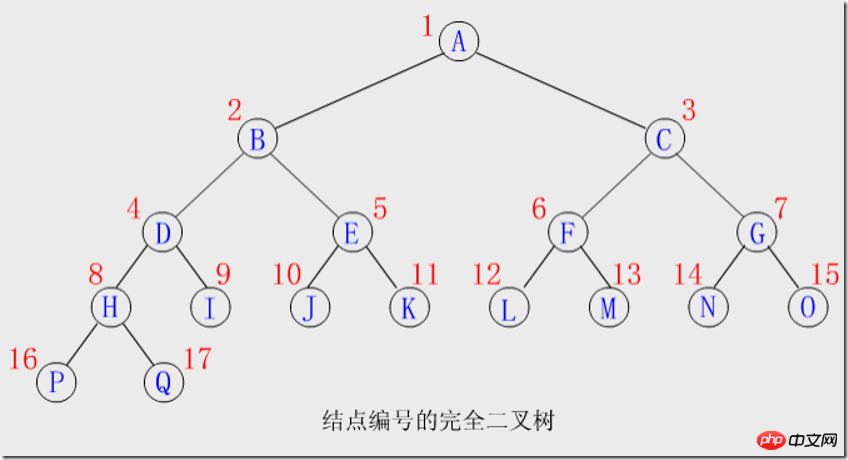
番号付け機能:

ノードの番号から、その親、左右の子、兄弟などの番号を導き出すことができます。 i 番号が付けられたノードが ki (1≤i≤n) であるとすると、

①i>1 の場合、ki の親番号は i/2、i=1 の場合、Ki はルートノード、親はありません。。

② 2i≤n の場合、Ki の左の子の番号は 2i であり、そうでない場合、Ki には左の子がありません、つまり、Ki は葉でなければなりません。したがって、完全な二分木において i > n/2 の番号が付けられたノードは葉ノードでなければなりません。

③ 2i+1≤n の場合、Ki の右の子の数は 2i+1 であり、そうでない場合、Ki には右の子がありません。

注: ki (0≤i≤n) が配列の添字を満たす場合、考えられる左と右の子はそれぞれ 2i+1 と 2i+2 になります。

ヒープソートのアイデア（例として大きなトップヒープを取り上げます）

ヒープのトップが最大のキーワードを記録するという機能を使用して、各ラウンドでヒープのトップ要素を取得し、それらを順序付き領域は選択ソートの各ラウンドに似ています。順序付き領域に最大値が配置され、ヒープソートは選択ソートの改良版と考えることができます。

並べ替えるキーワードの最初のシーケンス (R0、R1、R2...Rn) を、最初の順序付けされていない領域である上部ヒープに構築します。
ヒープ R[ の最上位要素を構築します。 0] 最後の要素 R[n] と交換すると、新しい無秩序領域 (R0、R1、R2、...Rn-1) と新しい順序領域 (Rn) が得られます。交換後の新しいヒープの先頭 R[0] はヒープのプロパティに違反する可能性があるため、現在の非順序領域 (R0、R1、R2、...Rn-1) を新しいヒープに合わせて調整する必要があります。
順序付けされた領域の要素の数が n-1 になるまで手順 2 と 3 を繰り返し、並べ替えプロセス全体が完了します。

フィルタリングアルゴリズム

PHPヒープソートの詳しい説明 //理解するのが最も難しい部分

目標: すべてのサブツリーがヒープである完全なバイナリツリー。これは、このバイナリツリーとノードの唯一の違いは、ヒープ構造を満たしていないことであることを意味します。 //非常に重要、非常に重要、非常に重要

以下に示すように:

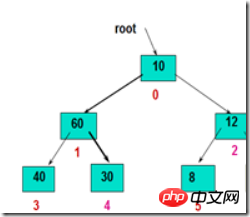clip_PHPヒープソートの詳しい説明002 方法: まずルートとその左右のサブツリーのルートノードを比較し、最大の要素をルートに交換します。次に、破壊されたパスに沿ってリーフノードまで調整すると、新しいヒープが得られます。

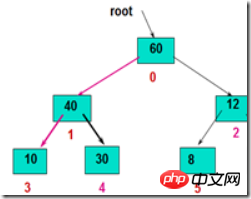clip_PHPヒープソートの詳しい説明003 応用例: 1. 上記のヒープソートの考え方において、手順2～3で未順序領域をヒープに調整する際に使用します。

2. ヒープを初期化します

最後の非リーフノード i (i=n/2、n はノードの数) から開始して、i をルートノードとするバイナリツリーは次のようになります。フィルタリングを通じてヒープに調整されます。最初の写真を例にとると、番号付けシーケンスは 8、7、6...1 です。

スクリーニングアルゴリズムの目標は、すべてのサブツリーがヒープである完全なバイナリツリーであるため、スクリーニングアルゴリズムの正確性は最後の非リーフノードから保証されます。

php实现堆排序：
<?php
//堆排序，对简单排序的改进
  function swap(array &$arr,$a,$b)
  {
      $temp=$arr[$a];
      $arr[$a]=$arr[$b];
      $arr[$b]=$temp;
  }
  //调整$arr[$start]的关键字，$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆（根节点最大的完全二叉树）
  //注意：这里节点s的左右孩子是 2*s +1 和 2*s+2(数组开始下标为0时)
   function HeapAdjust(array &$arr $start $end)
   {
       $temp= $arr[$start];
       //沿关键字较大的孩子节点向下筛选
       //左右孩子计算 （这里数组的开始下标为0）
       //左边孩子 2*$start+1,右边孩子 2*$start+2
       for ($j=2*$start+1; $j <=$end; $j=2*$j+1) { 
           if ($j !=$end &&$arr[$j] <$arr[$j+1]) {
               $j++;  //转化为右边孩子
           }
           if ($temp >=$arr[$j]) {
               break;  //已经满足大根堆
           }
           //将根节点设置为子节点的较大值
           $arr[$start]=$arr[$j];
           //继续往下
           $start=$j;
       }
       $arr[$start] =$temp;
   }
   function HeapSort(array &$arr)
   {
       $count=count($arr);
       //先将数据结构造成大根堆 （由于是完全二叉树，所以这里用floor($count/2-1),下标小于或等于这个数的节点都是有孩子的节点)
       for ($i=floor($count /2)-1; $i >=0 ; $i--) { 
           HeapAdjust($arr,$i,$count);
       }
       for ($i=$count-1; $i >=0 ; $i--) { 
       //将堆顶元素与最后一个元素交换，获取到最大元素(交换后的最后一个元素)，将最大元素放到数组末尾
           swap($arr,0,$i);
       //经过交换，将最后一个元素（最大元素）脱离大根堆，并将未经排序的新数（$arr[0...$i-1]）重新调整为大根堆
           HeapAdjust($arr,0,$i-1);
       }
   }
   $arr=array(4,1,5,9);
   HeapSort($arr);
   v

PHPヒープソートの詳しい説明

ヒープ配列の保存方法

ヒープソートのアイデア（例として大きなトップヒープを取り上げます）

スクリーニング アルゴリズムの目標は、すべてのサブツリーがヒープである完全なバイナリ ツリーであるため、スクリーニング アルゴリズムの正確性は最後の非リーフ ノードから保証されます。

関連記事

スクリーニングアルゴリズムの目標は、すべてのサブツリーがヒープである完全なバイナリツリーであるため、スクリーニングアルゴリズムの正確性は最後の非リーフノードから保証されます。