ホームページ >Java >&#&チュートリアル >最小全域ツリーの例の詳細な説明
最小全域ツリーの例の詳細な説明
- 零下一度オリジナル
- 2017-06-25 13:30:283571ブラウズ
最小スパニング ツリー - プリムのアルゴリズムとクラスカルのアルゴリズム
グラフのスパニング ツリーは、すべての頂点を含む非巡回接続サブグラフであり、重み付きグラフの最小スパニング ツリーは、最小の重みスパニング ツリーを持つグラフです。
プリムアルゴリズム
アルゴリズムの簡単な説明
1) 入力: 頂点セットが V でエッジセットが E である重み付き接続グラフ。 2). 初期化: Vnew
= {x}、x は集合 V 内の任意のノード (開始点)、Enew = {} は空です。3) 以下の操作を繰り返します。 V new = V まで:
a. 集合 E 内の最小の重みを持つエッジを選択します。ここで、u は集合 Vnew 内の要素であり、v は集合 E に含まれていません。 set Vnew、および v∈V (上記の条件を満たし、同じ重みを持つエッジが複数ある場合は、そのうちの 1 つを任意に選択できます)
b をセット Vnew に追加します。 、edge がセット Enew に追加されます 4) 出力: セット Vnew
と Enew を使用して、結果の最小スパニング ツリーを記述します。
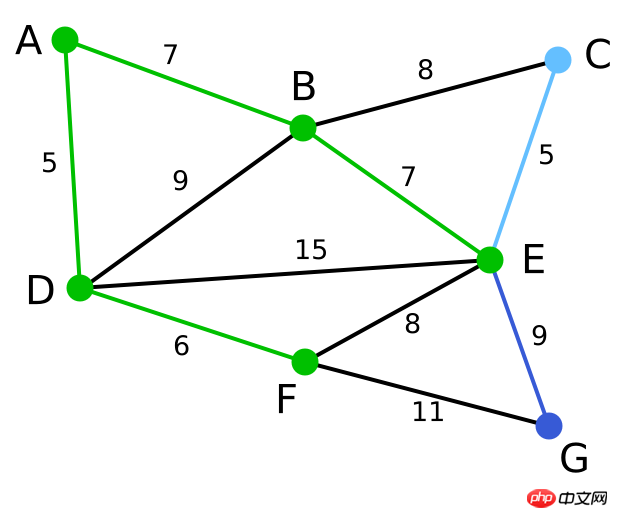
以下はアルゴリズムの凡例の説明です
凡例
説明
| オプション | 選択済み (V新規) | )|||
|---|---|---|---|---|
| は開始点として恣意的に選択されました。頂点 A、 B、 | は単一のエッジによって D に接続されています。 A | はDに最も近い頂点であるため、A | と対応するエッジADが強調表示されます。次へ 頂点は距離 D | またはA で最も近い頂点です。 B | は
| A から7、E | FはDまたはAに最も近いため、頂点Fと対応するエッジDFが強調表示されます。アルゴリズムは引き続き上記のステップを繰り返します。距離Aが7である頂点Bが強調表示されます。 CB、E、G | A、D、F | 現在の状況では、C、E、Gから選択できます。 CはBからの8、EはBからの7、GはFからの11です。 Eが最も近いので、頂点Eと対応するエッジBEが強調表示されます。 | なし | C、E、G | A、D、F、B |
|
|
ここで、選択できる頂点は のみです。 CとG。 CとEの間の距離は5、GとEの間の距離は9であるため、Cが選択され、エッジECとともに強調表示されます。 | なし | C、G | A、D、F、B、E |
|
頂点G は唯一残っている頂点です。 Fからの距離は11、Eからの距離は9、そしてEが最も近いので、Gと対応するエッジEGが強調表示されます。 | None | G | A、D、F、B、E、C |
|
これで、すべての頂点が選択されました、写真の緑色部分は、接続されたグラフの最小スパニング ツリーです。この例では、最小スパニング ツリーの重みの合計は 39 です。 | なし | なし | A、D、F、B、E、C、G |
アルゴリズムの実装については、『アルゴリズム』の第 4 版、または清華出版社の『データ構造 - Java 言語実装』を参照してください (実装方法はより明確で簡単です)
クラスカル アルゴリズム
1. 概要
クラスカルのアルゴリズムは、1956 年に Joseph Kruskal によって公開された、最小スパニング ツリーを見つけるために使用されるアルゴリズムです。同じ問題を解決するために使用される Prim アルゴリズムと Boruvka アルゴリズムもあります。 3 つのアルゴリズムはすべて、貪欲アルゴリズムの応用です。 Boruvka のアルゴリズムとの違いは、Kruskal のアルゴリズムはグラフ内に同じ重みを持つエッジが存在する場合にも有効であることです。
2. アルゴリズムの簡単な説明
1) Graph
2) に v 個の頂点と e 個のエッジがあることを思い出してください。 , Graphnew には元のグラフに同じ e 頂点がありますが、エッジはありません
3)。元のグラフ内のすべての e エッジを重みで小さいものから大きいものに並べ替えます4)。最小のエッジは、グラフ内のすべてのノードが同じ連結コンポーネント内に収まるまで、各エッジを横断し始めます。辺のエッジに接続されている 2 つのノードが、Graph
new
内に存在しません。
到 このエッジをグラフに追加してグラフにします
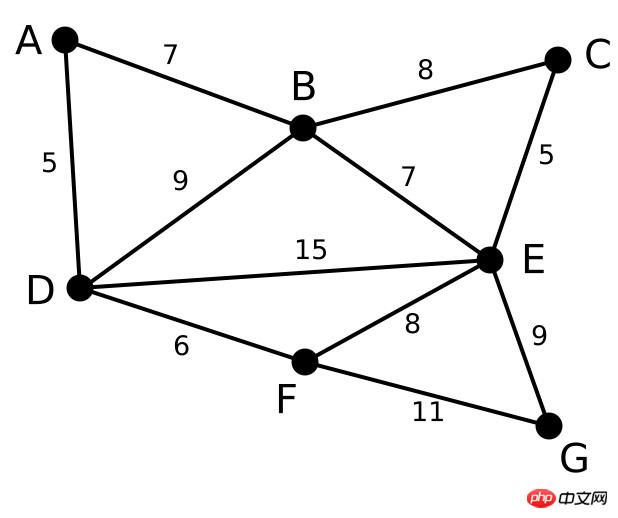

まず最初に、絵グラフがあります。いくつかの点とエッジです
すべてのエッジのすべてのエッジ 長さによって並べ替え、並べ替えられた結果をエッジの選択の基礎として使用します。ここでも貪欲なアルゴリズムの考え方が反映されています。 
用用到综合合) 局所最適リソースの選択 ソートが完了したら、最初にエッジADを選択します。このようにして、私たちの写真は右側の写真になります

次に、BC または EF の選択を続けますが、長さ 8 の辺が選択されていない最小の辺になります。しかし、現在は接続されています (BC は CE、EB、同様の EF は EB、BA、AD、DF を介して接続できます)。したがって、それらを選択する必要はありません。同様の BD も接続されています (上の図の接続線は赤で示されています)。
🎜結局、EGとFGだけが残りました。もちろんEGを選びました。 🎜🎜🎜🎜🎜🎜🎜🎜アルゴリズムの実装については、『アルゴリズム』第4版のコードを参照してください。 🎜🎜🎜以上が最小全域ツリーの例の詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。


 E
E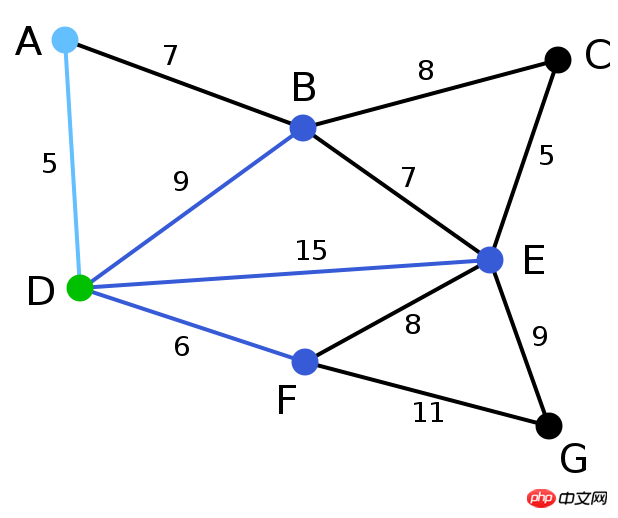 は15、
は15、