JavaScript画像処理—エッジ勾配計算機能_JavaScriptスキル

はじめに

前回の記事 では、画像処理における拡張関数と収縮関数について説明しました。今回はエッジの勾配計算関数について説明します。

画像の端

画像のエッジは数学的にどのように表現されますか?

画像の端では、隣接するピクセル値が大きく変化するはずです。数学では、微分は変化の速度を表現する方法です。グラデーション値の大きな変化は、画像の内容が大きく変化していることを示します。

より鮮明なイメージで説明するために、1 次元のグラフがあると仮定します。以下の画像の灰色の値の「ジャンプ」は、エッジの存在を示します:

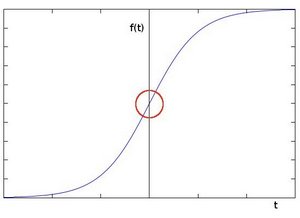
一次微分微分を使用すると、エッジの「ジャンプ」(ここでは高いピークとして示されています) の存在をより明確に確認できます。

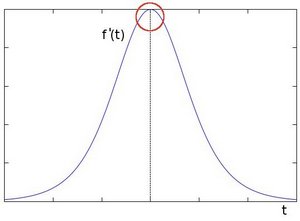
このことから、近傍よりも大きい勾配値を持つピクセルを見つけることでエッジを見つけることができると結論付けることができます。

おおよその勾配

例えばコアが3の場合。

まず、x 方向の近似導関数を計算します。

次に、y 方向の近似導関数を計算します。

次に勾配を計算します:

もちろん次のように書くこともできます:

関数の実装

コードをコピー

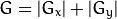
コードは次のとおりです。 🎜>

var Sobel = function(__src, __xorder, __yorder, __size, __borderType, __dst){
(__src && (__xorder ^ __yorder)) || error(arguments.callee, IS_UNDEFINED_OR_NULL/* { line} * /);
if(__src.type && __src.type === "CV_GRAY"){
var kernel1,
kernel2,
height = __src.row,
width = __src.col,
dst = __dst || new Mat(高さ, 幅, CV_16I, 1),
dstData = dst.data
サイズ = __size || {
ケース 1:
サイズ = 3;
ケース 3:
if(__xorder){
カーネル = [-1, 0, 1,
-2, 0, 2 ,
-1, 0, 1
];
}else if(__yorder){
カーネル = [-1, -2, -1,
, 0, 0,
, 2 , 1
];
}
ブレーク
ケース 5:
if(__xorder){
カーネル = [-1, -2, 0, 2, 1 、
-4、-8、0、8、4、
-6、-12、0、12、6、
-4、-8、0、8、4、
- 1, - 2, 0, 2, 1
]; else if(__yorder){
カーネル = [-1, -4, -6, -4, -1,
- 2、-8、-12、-8、-2、
、0、0、0、0、
、8、12、8、2、
、4、6、4、1
] ;
}
ブレーク;
デフォルト:
error(arguments.callee, UNSPPORT_SIZE/* {line} */); GRAY216IC1Filter(__src , サイズ, 高さ, 幅, カーネル, dstData, __borderType);

}else{
error(arguments.callee, UNSPPORT_DATA_TYPE/* {line} */); 🎜>return dst;
};


ここでは、カーネル サイズ 3 と 5 の Sobel 演算子のみが提供されています。主な理由は、カーネル 7 以上の計算が比較的遅いためです。
単一チャネルの 16 ビット符号付き整数行列を出力します。




コードをコピー

コードは次のとおりです:

function GRAY216IC1Filter(__src, size, height, width, kernel, dstData, __borderType){
var start = size >> 1;

var withBorderMat = copyMakeBorder(__src, start, start, 0, 0, __borderType);

var mData = withBorderMat.data,
mWidth = withBorderMat.col;

var i, j, y, x, c;
var newValue, nowX, offsetY, offsetI;

for(i = height; i--;){
offsetI = i * width; -;){
newValue = 0;
for(y = サイズ; y--;){
offsetY = (y i) * mWidth;
for(x = サイズ; x--; ){
nowX = x j;
newValue = (mData[offsetY nowX] * kernel[y * size x]);
}
}
dstData[j offsetI] = newValue; 🎜>}
}
}


そしてこのフィルターにカーネルと行列を与えればOKです。

このフィルターを独立させた理由は、ラプラシアン演算子やシャール演算子など、他の同様の計算エッジ関数に使用できるためです。

符号なし 8 ビット整数に変換します

Sobel 演算子は 16 ビット符号付き整数を計算し、画像として表示できないため、それを符号なし 8 ビット整数行列に変換する関数が必要です。

convertScaleAbs 関数は、各要素の絶対値を取得し、それを Int8Array 配列に代入します。これは、代入中に 255 より大きい数値は自動的に 255 に変換され、0 未満の数値は自動的に 0 に変換されます。したがって、この作業を処理する関数を作成する必要はありません。

コードをコピー コードは次のとおりです。

function ConvertScaleAbs(__src, __dst){

__src || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
var height = __src.row,
width = __src.col,
channel = __src.channel,
sData = __src.data;

if(!__dst){
if(channel === 1)
dst = new Mat(高さ, 幅, CV_GRAY); if(チャンネル === 4)
dst = 新しい Mat(高さ, 幅, CV_RGBA);
else
dst = 新しい Mat(高さ, 幅, CV_8I, チャンネル);
dst = __dst;
}

var dData = dst.data;

for(i = 高さ; i --; ){
for(j = width * チャネル; j--;){
dData[i * width * チャネル j] = Math.abs(sData[i * width * チャネル j]);
}
}

dst を返す
}



値を比例的に結合します

x方向の勾配計算値とy方向の勾配計算値を重ね合わせる関数も必要です。

コードをコピー

コードは次のとおりです。var addWeighted = function(__src1, __alpha, __src2, __beta , __gamma, __dst){ (__src1 && __src2) || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */); var height = __src1.row, width = __src1.col 、

alpha = __alpha || 0、

beta = __beta || 0、
gamma = __gamma || 0; == __src2 .row || width !== __src2.col || チャネル !== __src2.channel){
error(arguments.callee, "Src2 は src1 と同じサイズおよびチャネル番号でなければなりません!"/* {line} */);
return null;
}

if(!__dst){
if(__src1.type.match(/CV_d /))
dst = new Mat( 高さ, 幅, __src1. Depth(), チャンネル);
else
dst = new Mat(高さ, 幅, __src1. Depth()); __dst;
}

var dData = dst.data、
s1Data = __src1.data、
s2Data = __src2.data; 🎜>for (i = 高さ * 幅 * チャネル; i--;)
dData[i] = __alpha * s1Data[i] __beta * s2Data[i] gamma;

return };


この関数は実際には、2 つの行列の対応する要素を固定の比率で加算するだけです。
レンダリング