ホームページ >バックエンド開発 >PHPチュートリアル >グラフエッジの重みを変更する
グラフエッジの重みを変更する
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBオリジナル
- 2024-08-31 06:35:321384ブラウズ
2699。グラフエッジの重みを変更
難易度: 難しい
トピック: グラフ、ヒープ (優先キュー)、最短パス
0 から n - 1 までのラベルが付いた n 個のノードと、edges[i] = [ai, b の整数配列edges を含む無向重み接続グラフが与えられます。 i, wi] は、ノード ai と bi の間に重み wi.
一部のエッジの重みは -1 (wi = -1) ですが、他のエッジの重みは 正 (wi > 0) です。 .
あなたのタスクは、範囲 [1, 2 * 109 の 正の整数値を割り当てて、すべてのエッジを -1 の重みで変更することです。 ] ノードのソースと宛先間の最短距離が整数のターゲットと等しくなるようにします。ソースと宛先間の最短距離をターゲットと等しくする複数の変更がある場合、それらのどれもが正しいとみなされます。
ソースから宛先までの最短距離をターゲットと等しくすることができる場合は、すべてのエッジ (未変更のエッジも含む) を任意の順序で含む配列を返し、それが不可能な場合は 空の配列 を返します。 .
注: 初期の正の重みを使用してエッジの重みを変更することはできません。
例 1:
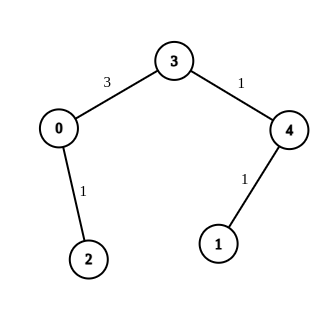
- 入力: n = 5、エッジ = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1] ]、ソース = 0、宛先 = 1、ターゲット = 5
- 出力: [[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
- 説明: 上のグラフは、0 から 1 までの距離を 5 に等しくする、エッジへの可能な変更を示しています。
例 2:
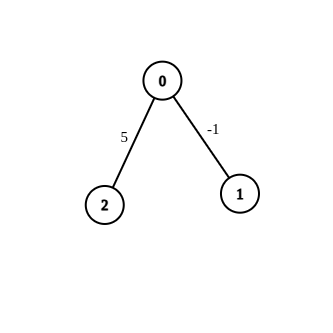
- 入力: n = 3、エッジ = [[0,1,-1],[0,2,5]]、ソース = 0、宛先 = 2、ターゲット = 6
- 出力: []
- 説明: 上のグラフには初期エッジが含まれています。重み -1 でエッジを変更しても、0 から 2 までの距離を 6 に等しくすることはできません。したがって、空の配列が返されます。
例 3:
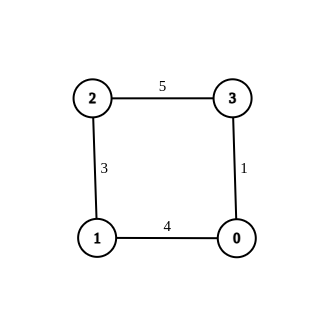
- 入力: n = 4、エッジ = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]]、ソース= 0、目的地 = 2、ターゲット = 6
- 出力: [[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
- 説明: 上のグラフは、0 から 2 までの最短距離が 6 である変更されたグラフを示しています。
制約:
- 1
1
edges[i].length == 3
- 0 i, bi < n w
- i = -1 または 1 <= wi <= 107 a
- i != bi 0 <= 送信元、送信先
- n
- 送信元 != 宛先
- 1 <= ターゲット <= 109
- グラフは接続されており、自己ループや繰り返しエッジはありません
ヒント:
- まず、ソースから宛先までの最短パスをターゲットと等しくすることが実際に可能であることを確認します。
- 変更されるエッジを含まないソースから宛先までの最短パスがターゲットより小さい場合、それは不可能です。
- 変更対象のエッジを含み、それらに一時的な重み 1 を割り当てた、ソースから宛先までの最短パスがターゲットよりも大きい場合も、これは不可能です。
- ソースから u までの最短パスの長さ (dis1) に、v から宛先までの最短パスの長さ (dis2) を加えたものがターゲット (dis1) よりも小さくなるような、変更可能なエッジ (u, v) を見つけることができるとします。 + dis2 < target) の場合、その重みを「target - dis1 - dis2」に変更できます。
- まだ重み「-1」を持つ他のすべてのエッジについては、重みを十分に大きな数値 (ターゲット、ターゲット + 1、または 200000000 など) に変更します。
解決策:
このアプローチは次のように分解できます:
アプローチ:
-
既存の重みによる初期チェック:
- まず、正の重みを持つエッジのみを使用し、重み -1 を持つエッジを無視して、ソースから宛先までの最短パスを計算します。
- この距離がすでにターゲットより大きい場合、-1 エッジを変更してターゲットを達成することは不可能であるため、空の配列を返します。
-
重み 1 の一時的な割り当て:
- 次に、重み -1 を持つすべてのエッジに一時的な重み 1 を割り当て、最短パスを再計算します。
- この最短パスが依然としてターゲットより大きい場合は、ターゲットを達成することは不可能であるため、空の配列を返します。
-
特定のエッジの重みを変更:
- 重み -1 のエッジを反復処理し、ターゲットの距離に正確に一致するように調整できるエッジを特定します。これは、このエッジに至るパスとこのエッジからのパスの合計距離が正確なターゲット距離になるように、エッジの重みを調整することによって行われます。
- 残りの -1 エッジには、最短パスに影響を与えないように、十分大きな重み (例: 2 * 10^9) を割り当てます。
-
変更されたエッジを返す:
- 最後に、変更されたエッジのリストを返します。
このソリューションを PHP で実装してみましょう: 2699。グラフエッジの重みを変更
説明:
- ダイクストラ関数は、ソースから他のすべてのノードまでの最短パスを計算します。
- 最初に -1 エッジを無視して最短パスを計算します。
- -1 エッジのないパスがターゲットより小さい場合、関数は空の配列を返し、ターゲットを満たすように重みを調整することが不可能であることを示します。
- それ以外の場合は、-1 のエッジをすべて一時的に 1 に設定し、最短パスがターゲットを超えるかどうかを確認します。
- そうなった場合、再びターゲットに到達することは不可能となり、空の配列が返されます。
- 次に、-1 エッジの重みを戦略的に変更して、正確にターゲットの最短パスを実現します。
このアプローチでは、エッジの重みを効率的にチェックして調整し、可能であればターゲット距離が確実に満たされるようにします。
連絡先リンク
このシリーズが役立つと思われた場合は、GitHub で リポジトリ にスターを付けるか、お気に入りのソーシャル ネットワークで投稿を共有することを検討してください。あなたのサポートは私にとって大きな意味を持ちます!
このような役立つコンテンツがさらに必要な場合は、お気軽にフォローしてください:
- GitHub
以上がグラフエッジの重みを変更するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

