ホームページ >Java >&#&チュートリアル >グラフのモデリング
グラフのモデリング
- 王林オリジナル
- 2024-08-10 07:06:32710ブラウズ
Graph インターフェイスは、グラフの一般的な操作を定義します。 Java Collections Framework は、複雑なデータ構造を設計するための良い例として機能します。データ構造の共通機能は、次に示すようにインターフェース (例: Collection、Set、List、Queue) で定義されます。図20.1。抽象クラス (例: AbstractCollection、AbstractSet、AbstractList) はインターフェースを部分的に実装します。具象クラス (例: HashSet、LinkedHashSet、TreeSet、ArrayList、LinkedList、PriorityQueue) 具体的な実装を提供します。この設計パターンは、グラフのモデリングに役立ちます。グラフのすべての一般的な操作を含む Graph という名前のインターフェイスと、Graph インターフェイスを部分的に実装する AbstractGraph という名前の抽象クラスを定義します。多くの具体的なグラフをデザインに追加できます。たとえば、UnweightedGraph および WeightedGraph という名前のグラフを定義します。これらのインターフェースとクラスの関係を以下の図に示します。
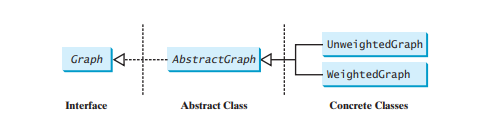
グラフの一般的な操作は何ですか?一般に、グラフ内の頂点の数を取得する、グラフ内のすべての頂点を取得する、指定されたインデックスを持つ頂点オブジェクトを取得する、指定された名前を持つ頂点のインデックスを取得する、頂点の近傍を取得する、頂点の次数、グラフのクリア、新しい頂点の追加、新しいエッジの追加、深さ優先検索の実行、および幅優先検索の実行。深さ優先検索と幅優先検索については、次のセクションで紹介します。以下の図は、これらのメソッドを UML 図で示しています。
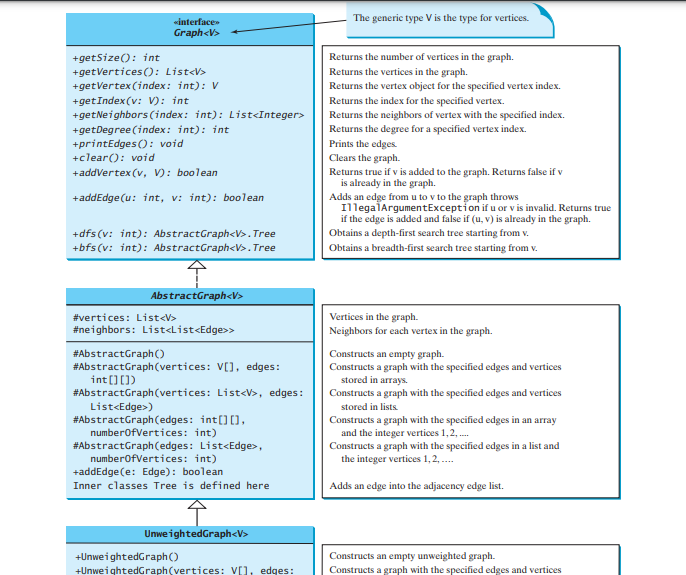
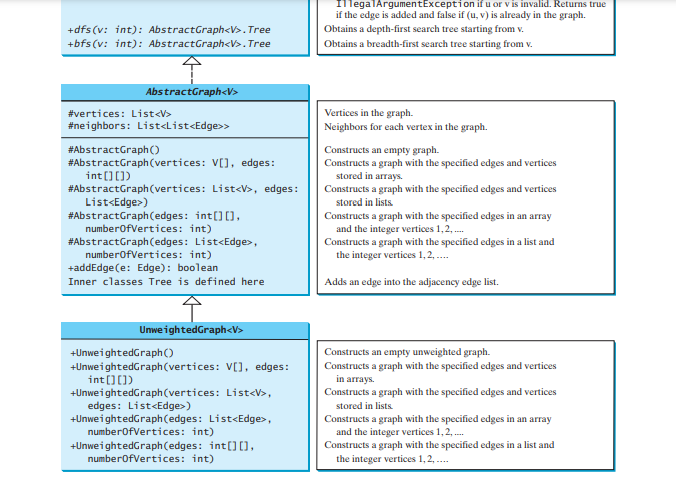
AbstractGraph は新しいメソッドを導入しません。頂点のリストとエッジ隣接リストは、AbstractGraph クラスで定義されます。これらのデータ フィールドを使用すると、Graph インターフェイスで定義されたすべてのメソッドを実装するだけで十分です。便宜上、グラフは単純なグラフであると仮定します。つまり、頂点にはそれ自体へのエッジがなく、頂点 u から v までの平行なエッジはありません。
AbstractGraph は Graph のすべてのメソッドを実装しており、addEdge(edge) メソッドを除いて新しいメソッドは導入していません。 >Edge オブジェクトを隣接エッジ リストに追加します。 UnweightedGraph は、具体的な Graph インスタンスを作成するための 5 つのコンストラクターを使用して AbstractGraph を単純に拡張します。
任意の種類の頂点を使用してグラフを作成できます。各頂点はインデックスに関連付けられます。インデックスは、頂点リスト内の頂点のインデックスと同じです。頂点を指定せずにグラフを作成した場合、頂点はインデックスと同じになります。
AbstractGraph クラスは、Graph インターフェイスのすべてのメソッドを実装します。では、なぜ抽象的なものとして定義されるのでしょうか?将来的には、AbstractGraph では実装できない新しいメソッドを Graph インターフェイスに追加することが必要になる可能性があります。クラスの保守を容易にするために、AbstractGraph クラスを抽象として定義することが望ましいです。
public class TestGraph {
public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};
// Edge array for graph
int[][] edges = {
{0, 1}, {0, 3}, {0, 5},
{1, 0}, {1, 2}, {1, 3},
{2, 1}, {2, 3}, {2, 4}, {2, 10},
{3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
{4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
{5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
{6, 5}, {6, 7},
{7, 4}, {7, 5}, {7, 6}, {7, 8},
{8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
{9, 8}, {9, 11},
{10, 2}, {10, 4}, {10, 8}, {10, 11},
{11, 8}, {11, 9}, {11, 10}
};
Graph<String> graph1 = new UnweightedGraph<>(vertices, edges);
System.out.println("The number of vertices in graph1: " + graph1.getSize());
System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
System.out.println("The edges for graph1:");
graph1.printEdges();
// List of Edge objects for graph
String[] names = {"Peter", "Jane", "Mark", "Cindy", "Wendy"};
java.util.ArrayList<AbstractGraph.Edge> edgeList = new java.util.ArrayList<>();
edgeList.add(new AbstractGraph.Edge(0, 2));
edgeList.add(new AbstractGraph.Edge(1, 2));
edgeList.add(new AbstractGraph.Edge(2, 4));
edgeList.add(new AbstractGraph.Edge(3, 4));
// Create a graph with 5 vertices
Graph<String> graph2 = new UnweightedGraph<>(java.util.Arrays.asList(names), edgeList);
System.out.println("\nThe number of vertices in graph2: " + graph2.getSize());
System.out.println("Te edges for graph2:");
graph2.printEdges();
}
}
グラフ1の頂点の数: 12
インデックス 1 の頂点はサンフランシスコです
マイアミの指数は 9
グラフ 1 のエッジ:
シアトル (0): (0, 1) (0, 3) (0, 5)
サンフランシスコ (1): (1, 0) (1, 2) (1, 3)
ロサンゼルス (2): (2, 1) (2, 3) (2, 4) (2, 10)
デンバー (3): (3, 0) (3, 1) (3, 2) (3, 4) (3, 5)
カンザスシティ (4): (4, 2) (4, 3) (4, 5) (4, 7) (4, 8) (4, 10)
シカゴ (5): (5, 0) (5, 3) (5, 4) (5, 6) (5, 7)
ボストン (6): (6, 5) (6, 7)
ニューヨーク (7): (7, 4) (7, 5) (7, 6) (7, 8)
アトランタ (8): (8, 4) (8, 7) (8, 9) (8, 10) (8, 11)
マイアミ (9): (9, 8) (9, 11)
ダラス (10): (10, 2) (10, 4) (10, 8) (10, 11)
ヒューストン (11): (11, 8) (11, 9) (11, 10)
The number of vertices in graph2: 5
The edges for graph2:
Peter (0): (0, 2)
Jane (1): (1, 2)
Mark (2): (2, 4)
Cindy (3): (3, 4)
Wendy (4):
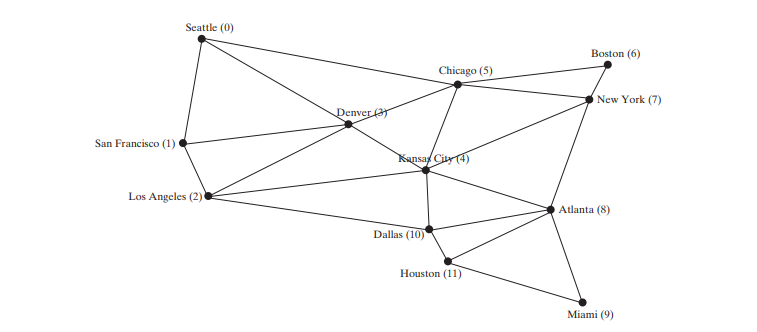
The program creates graph1 for the graph in Figure 28.1 in lines 3–23. The vertices for graph1 are defined in lines 3–5. The edges for graph1 are defined in 8–21. The edges are represented using a two-dimensional array. For each row i in the array, edges[i][0] and edges[i][1] indicate that there is an edge from vertex edges[i][0] to vertex edges[i][1]. For example, the first row, {0, 1}, represents the edge from vertex 0 (edges[0][0]) to vertex 1 (edges[0][1]). The row {0, 5} represents the edge from vertex 0 (edges[2][0]) to vertex 5 (edges[2][1]). The graph is created in line 23. Line 31 invokes the printEdges() method on graph1 to display all edges in graph1.
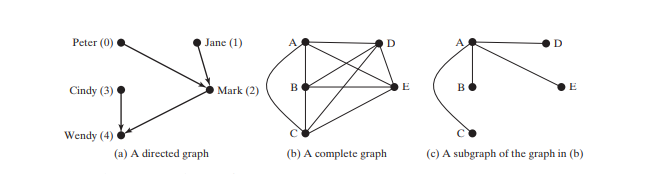
The program creates graph2 for the graph in Figure 28.3a in lines 34–43. The edges for graph2 are defined in lines 37–40. graph2 is created using a list of Edge objects in line 43. Line 47 invokes the printEdges() method on graph2 to display all edges in graph2.
Note that both graph1 and graph2 contain the vertices of strings. The vertices are associated with indices 0, 1, . . . , n-1. The index is the location of the vertex in vertices. For example, the index of vertex Miami is 9.
Now we turn our attention to implementing the interface and classes. The codes below give the Graph interface, the AbstractGraph class, and the UnweightedGraph class, respectively.
public interface Graph<V> {
/** Return the number of vertices in the graph */
public int getSize();
/** Return the vertices in the graph */
public java.util.List<V> getVertices();
/** Return the object for the specified vertex index */
public V getVertex(int index);
/** Return the index for the specified vertex object */
public int getIndex(V v);
/** Return the neighbors of vertex with the specified index */
public java.util.List<Integer> getNeighbors(int index);
/** Return the degree for a specified vertex */
public int getDegree(int v);
/** Print the edges */
public void printEdges();
/** Clear the graph */
public void clear();
/** Add a vertex to the graph */
public void addVertex(V vertex);
/** Add an edge to the graph */
public void addEdge(int u, int v);
/** Obtain a depth-first search tree starting from v */
public AbstractGraph<V>.Tree dfs(int v);
/** Obtain a breadth-first search tree starting from v */
public AbstractGraph<V>.Tree bfs(int v);
}
import java.util.*;
public abstract class AbstractGraph<V> implements Graph<V> {
protected List<V> vertices = new ArrayList<>(); // Store vertices
protected List<List<Edge>> neighbors = new ArrayList<>(); // Adjacency lists
/** Construct an empty graph */
protected AbstractGraph() {}
/** Construct a graph from vertices and edges stored in arrays */
protected AbstractGraph(V[] vertices, int[][] edges) {
for(int i = 0; i < vertices.length; i++)
addVertex(vertices[i]);
createAdjacencyLists(edges, vertices.length);
}
/** Construct a graph from vertices and edges stored in List */
protected AbstractGraph(List<V> vertices, List<Edge> edges) {
for(int i = 0; i < vertices.size(); i++)
addVertex(vertices.get(i));
createAdjacencyLists(edges, vertices.size());
}
/** Construct a graph for integer vertices 0, 1, 2 and edge list */
protected AbstractGraph(List<Edge> edges, int numberOfVertices) {
for(int i = 0; i < numberOfVertices; i++)
addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}
createAdjacencyLists(edges, numberOfVertices);
}
/** Construct a graph from integer vertices 0, 1, and edge array */
protected AbstractGraph(int[][] edges, int numberOfVertices) {
for(int i = 0; i < numberOfVertices; i++)
addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}
createAdjacencyLists(edges, numberOfVertices);
}
/** Create adjacency lists for each vertex */
private void createAdjacencyLists(int[][] edges, int numberOfVertices) {
for(int i = 0; i < edges.length; i++) {
addEdge(edges[i][0], edges[i][1]);
}
}
/** Create adjacency lists for each vertex */
private void createAdjacencyLists(List<Edge> edges, int numberOfVertices) {
for(Edge edge: edges) {
addEdge(edge.u, edge.v);
}
}
@Override /** Return the number of vertices in the graph */
public int getSize() {
return vertices.size();
}
@Override /** Return the vertices in the graph */
public List<V> getVertices() {
return vertices;
}
@Override /** Return the object for the specified vertex */
public V getVertex(int index) {
return vertices.get(index);
}
@Override /** Return the index for the specified vertex object */
public int getIndex(V v) {
return vertices.indexOf(v);
}
@Override /** Return the neighbors of the specified vertex */
public List<Integer> getNeighbors(int index) {
List<Integer> result = new ArrayList<>();
for(Edge e: neighbors.get(index))
result.add(e.v);
return result;
}
@Override /** Return the degree for a specified vertex */
public int getDegree(int v) {
return neighbors.get(v).size();
}
@Override /** Print the edges */
public void printEdges() {
for(int u = 0; u < neighbors.size(); u++) {
System.out.print(getVertex(u) + " (" + u + "): ");
for(Edge e: neighbors.get(u)) {
System.out.print("(" + getVertex(e.u) + ", " + getVertex(e.v) + ") ");
}
System.out.println();
}
}
@Override /** Clear the graph */
public void clear() {
vertices.clear();
neighbors.clear();
}
@Override /** Add a vertex to the graph */
public void addVertex(V vertex) {
if(!vertices.contains(vertex)) {
vertices.add(vertex);
neighbors.add(new ArrayList<Edge>());
}
}
/** Add an edge to the graph */
protected boolean addEdge(Edge e) {
if(e.u < 0 || e.u > getSize() - 1)
throw new IllegalArgumentException("No such index: " + e.u);
if(e.v < 0 || e.v > getSize() - 1)
throw new IllegalArgumentException("No such index: " + e.v);
if(!neighbors.get(e.u).contains(e)) {
neighbors.get(e.u).add(e);
return true;
}
else {
return false;
}
}
@Override /** Add an edge to the graph */
public void addEdge(int u, int v) {
addEdge(new Edge(u, v));
}
/** Edge inner class inside the AbstractGraph class */
public static class Edge {
public int u; // Starting vertex of the edge
public int v; // Ending vertex of the edge
/** Construct an edge for (u, v) */
public Edge(int u, int v) {
this.u = u;
this.v = v;
}
public boolean equals(Object o) {
return u == ((Edge)o).u && v == ((Edge)o).v;
}
}
@Override /** Obtain a DFS tree starting from vertex v */
public Tree dfs(int v) {
List<Integer> searchOrder = new ArrayList<>();
int[] parent = new int[vertices.size()];
for(int i = 0; i < parent.length; i++)
parent[i] = -1; // Initialize parent[i] to -1
// Mark visited vertices
boolean[] isVisited = new boolean[vertices.size()];
// Recursively search
dfs(v, parent, searchOrder, isVisited);
// Return a search tree
return new Tree(v, parent, searchOrder);
}
/** Recursive method for DFS search */
private void dfs(int u, int[] parent, List<Integer> searchOrder, boolean[] isVisited) {
// Store the visited vertex
searchOrder.add(u);
isVisited[u] = true; // Vertex v visited
for(Edge e: neighbors.get(u)) {
if(!isVisited[e.v]) {
parent[e.v] = u; // The parent of vertex e.v is u
dfs(e.v, parent, searchOrder, isVisited); // Recursive search
}
}
}
@Override /** Starting bfs search from vertex v */
public Tree bfs(int v) {
List<Integer> searchOrder = new ArrayList<>();
int[] parent = new int[vertices.size()];
for(int i = 0; i < parent.length; i++)
parent[i] = -1; // Initialize parent[i] to -1
java.util.LinkedList<Integer> queue = new java.util.LinkedList<>(); // list used as queue
boolean[] isVisited = new boolean[vertices.size()];
queue.offer(v); // Enqueue v
isVisited[v] = true; // Mark it visited
while(!queue.isEmpty()) {
int u = queue.poll(); // Dequeue to u
searchOrder.add(u); // u searched
for(Edge e: neighbors.get(u)) {
if(!isVisited[e.v]) {
queue.offer(e.v); // Enqueue w
parent[e.v] = u; // The parent of w is u
isVisited[e.v] = true; // Mark it visited
}
}
}
return new Tree(v, parent, searchOrder);
}
/** Tree inner class inside the AbstractGraph class */
public class Tree {
private int root; // The root of the tree
private int[] parent; // Store the parent of each vertex
private List<Integer> searchOrder; // Store the search order
/** Construct a tree with root, parent, and searchOrder */
public Tree(int root, int[] parent, List<Integer> searchOrder) {
this.root = root;
this.parent = parent;
this.searchOrder = searchOrder;
}
/** Return the root of the tree */
public int getRoot() {
return root;
}
/** Return the parent of vertex v */
public int getParent(int v) {
return parent[v];
}
/** Return an array representing search order */
public List<Integer> getSearchOrder() {
return searchOrder;
}
/** Return number of vertices found */
public int getNumberOfVerticesFound() {
return searchOrder.size();
}
/** Return the path of vertices from a vertex to the root */
public List<V> getPath(int index) {
ArrayList<V> path = new ArrayList<>();
do {
path.add(vertices.get(index));
index = parent[index];
}
while(index != -1);
return path;
}
/** Print a path from the root vertex v */
public void printPath(int index) {
List<V> path = getPath(index);
System.out.print("A path from " + vertices.get(root) + " to " + vertices.get(index) + ": ");
for(int i = path.size() - 1; i >= 0; i--)
System.out.print(path.get(i) + " ");
}
/** Print the whole tree */
public void printTree() {
System.out.println("Root is: " + vertices.get(root));
System.out.print("Edges: ");
for(int i = 0; i < parent.length; i++) {
if(parent[i] != -1) {
// Display an edge
System.out.print("(" + vertices.get(parent[i]) + "' " + vertices.get(i) + ") ");
}
}
System.out.println();
}
}
}
import java.util.*;
public class UnweightedGraph<V> extends AbstractGraph<V> {
/** Construct an empty graph */
public UnweightedGraph() {}
/** Construct a graph from vertices and edges stored in arrays */
public UnweightedGraph(V[] vertices, int[][] edges) {
super(vertices, edges);
}
/** Construct a graph from vertices and edges stored in List */
public UnweightedGraph(List<V> vertices, List<Edge> edges) {
super(vertices, edges);
}
/** Construct a graph for integer vertices 0, 1, 2, and edge list */
public UnweightedGraph(List<Edge> edges, int numberOfVertices) {
super(edges, numberOfVertices);
}
/** Construct a graph from integer vertices 0, 1, and edge array */
public UnweightedGraph(int[][] edges, int numberOfVertices) {
super(edges, numberOfVertices);
}
}
The code in the Graph interface and the UnweightedGraph class are straightforward. Let us digest the code in the AbstractGraph class.
The AbstractGraph class defines the data field vertices (line 4) to store vertices and neighbors (line 5) to store edges in adjacency lists. neighbors.get(i) stores all edges adjacent to vertex i. Four overloaded constructors are defined in lines 9–42 to create a default graph, or a graph from arrays or lists of edges and vertices. The createAdjacencyLists(int[][] edges, int numberOfVertices) method creates adjacency lists from edges in an array (lines 45–50). The createAdjacencyLists(List edges, int numberOfVertices) method creates adjacency lists from edges in a list (lines 53–58).
The getNeighbors(u) method (lines 81–87) returns a list of vertices adjacent to vertex u. The clear() method (lines 106–110) removes all vertices and edges from the graph. The addVertex(u) method (lines 112–122) adds a new vertex to vertices and returns true. It returns false if the vertex is already in the graph (line 120).
The addEdge(e) method (lines 124–139) adds a new edge the adjacency edge list and returns true. It returns false if the edge is already in the graph. This method may throw IllegalArgumentException if the edge is invalid (lines 126–130).
The printEdges() method (lines 95–104) displays all vertices and edges adjacent to each vertex.
The code in lines 164–293 gives the methods for finding a depth-first search tree and a breadth-first search tree, which will be introduced in Depth-First Search (DFS) and Breadth-First Search (BFS), respectively.
以上がグラフのモデリングの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

