ホームページ >テクノロジー周辺機器 >AI >DeepMind が量子化学計算用のニューラル ネットワーク変分モンテカルロを開発
DeepMind が量子化学計算用のニューラル ネットワーク変分モンテカルロを開発
- PHPzオリジナル
- 2024-07-16 15:26:30581ブラウズ

ここでは、DeepMind とインペリアル カレッジ ロンドンの研究者が、最近開発された基底関数に依存しないフェルミオニック ニューラル ネットワーク (FermiNet) 波動関数を使用して、この問題に取り組んでいます。 FermiNet は、さまざまな定性的な陽電子結合特性を持つ、さまざまな原子や小分子に高精度の、場合によっては最先端の基底状態エネルギーを生成することが判明しました。
研究者らは、挑戦的な非極性ベンゼン分子の結合エネルギーを計算し、実験値との良好な一致を発見し、明示的に相関したガウス波動関数を使用して得られたものよりも好ましい消滅率を得ました。この結果は、ニューラル ネットワークの波動関数に基づく方法の一般的な利点を実証し、標準的な分子ハミルトニアン以外のシステムに適用します。
関連する研究は「陽電子化学のためのニューラルネットワーク変分モンテカルロ」と題され、6月18日に「Nature Communications」に掲載されました。
論文リンク: https://www.nature.com/articles/s41467-024-49290-1 大量の陽電子を捕捉するための実験装置の進歩により、陽電子の結合状態を記述するためのより効率的な計算ツールの開発が推進されました。反物質技術の革新を加速します。  陽電子分子錯体の基底状態特性の量子化学計算は困難です。主な困難は、電子と陽電子間の合体を表現するために適切な基底関数を使用することにあります。
陽電子分子錯体の基底状態特性の量子化学計算は困難です。主な困難は、電子と陽電子間の合体を表現するために適切な基底関数を使用することにあります。
ここで研究者らは、QMC 用に最近開発されたニューラル ネットワークの波動関数の仮定に基づいて、分子の陽電子束縛状態の基底状態特性を計算する新しい方法を提案します。フェルミオン ニューラル ネットワーク (FermiNet) は、一連の基底関数を参照せずに多体波動関数をモデル化します。これにより、陽電子波動関数を記述する際の上記の困難の多くが都合よく回避されます。
研究者らは、波動関数の陽電子成分を電子成分と同等に表現できるように FermiNet を拡張しました。ニューラル ネットワーク アーキテクチャに最小限の変更を加えるだけで、柔軟かつ正確なハイブリッド電子陽電子波動関数の仮定を取得できます。陽電子結合エネルギーと消滅速度は、異なる陽電子結合機構を備えた一連の系について計算され、これらの系の基底状態エネルギーについて最も高い精度が得られました。
陽電子水素化物、ナトリウム原子とマグネシウム原子、小さな二原子分子に関する結果は、この方法が以前の研究と比較して最先端の精度を達成できることを示しています。さらに、非極性ダイリチウムおよびベンゼン分子の結果は、強い電子-陽電子相関効果によって完全に制御される陽電子結合モードを記述するときにこの精度が保たれることを示しています。
下の図は、非極性分子と陽電子の間の結合メカニズムを直観的に理解するものです。相関支配的な結合は、分子の核から離れた電子密度の増加した中心によって促進されます。ダイリチウムではこれは共有結合であり、ベンゼンでは環内のπ結合の非局在化による分子中心の電子密度の増加です。
図: 陽電子リチウムとベンゼンの基底状態の単一粒子密度。 (出典: 論文) この方法で得られたベンゼンの陽電子結合エネルギーは、クイーンズ大学の Hofierka らの実験値および多体理論に非常に近いです。そして、得られた消滅率は、アルカリ金属原子や小分子の高精度 ECG-SVM 計算に匹敵します。さらに、FermiNet 波動関数を使用して蓄積された陽電子原子および分子の 2γ 消滅率を、他のさまざまな計算方法で得られた結果と比較すると、次の表のようになります。  表: 他のさまざまな計算方法で得られた消滅率との比較FermiNet 波動関数を使用して蓄積された陽電子原子および分子の比率、2γ 消滅率。 (出典: 論文)
表: 他のさまざまな計算方法で得られた消滅率との比較FermiNet 波動関数を使用して蓄積された陽電子原子および分子の比率、2γ 消滅率。 (出典: 論文)
1. 他の方法と比較して、ECG-SVM は波動関数を最もよく捉える特徴を構築することによって消滅率を計算します。 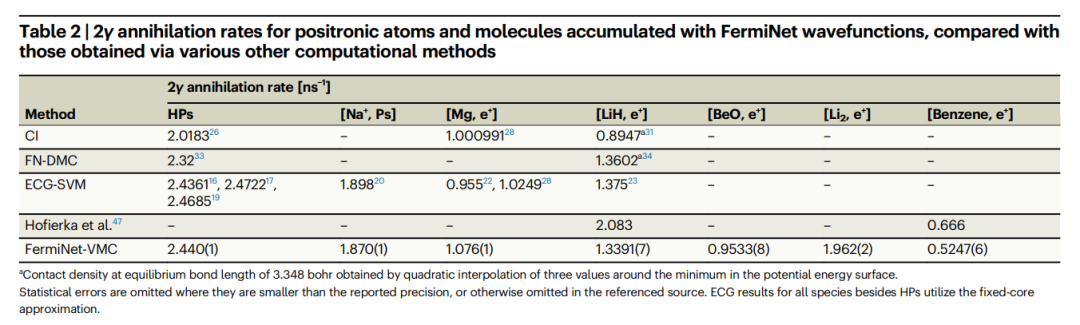
- 要約すると、ECG-SVM メソッドは、システム固有の調整を行わずに、さまざまな陽電子結合機構を持つさまざまな分子に対して高精度の結果を生成します。
以上がDeepMind が量子化学計算用のニューラル ネットワーク変分モンテカルロを開発の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

