複合材料中の原子拡散を研究し、UC がニューラル ネットワーク ダイナミクス手法を開発

編集者 | Green Luo

風に乗って顔に広がる花の香りと同じように、物質中の原子や分子も「拡散」しています。

材料中の分散は、析出、新しい相の形成、微細構造の進化のダイナミクスを決定し、機械的および物理的特性に大きな影響を与えます。複雑な組成をもつ材料の固有の化学的複雑さは、原子拡散モデリングと化学的に規則正しい構造の形成に課題をもたらします。

これに関して、カリフォルニア大学の研究者らは、複雑な組成の材料における原子の拡散と、その結果として生じる微細構造の進化を予測するためのニューラルネットワークダイナミクス（NNK）法を提案しました。

このフレームワークは、人工ニューラル ネットワークと組み合わせた効率的な格子構造と化学的特性評価に基づいており、経路に依存するすべての移動障壁と単一原子ホッピングを正確に予測できます。スケーラブルな NNK フレームワークは、異常な特性を隠した広大な組み合わせ空間で拡散関連の特性を探索するための有望な新しい手段を提供します。

関連研究「組成的に複雑な材料における拡散多重度と化学的秩序を探索するためのニューラルネットワーク動力学」が、5月9日付けの「Nature Communications」に掲載されました。

論文リンク: https://www.nature.com/articles/s41467-024-47927-9

物質の拡散とモデリングの課題

ある場所から別の場所への原子の移動イオンの量は、析出や相核生成など、多くの重要なプロセスや挙動を制御します。

金属や合金では、拡散プロセスは結晶格子内の原子ホッピングを媒介する空孔や点欠陥に関連しています。力場または密度汎関数理論に基づく分子動力学 (MD) モデリングは、ナノ秒の時間スケールで原子の拡散メカニズムを調査できますが、遅い拡散力学によって引き起こされる微細構造の変化は取得できないことがよくあります。

kMCシミュレーション法は、拡散媒介構造進化をシミュレーションするために使用される手法です。 kMC シミュレーションでは、遷移状態探索の計算コストが高いため、通常、主要なパラメーターは連続体モデルからパラメーター化されます。

高エントロピー合金と呼ばれることが多い組成的に複雑な合金（CCA）の出現は、化学的短距離秩序化、析出、偏析、放射欠陥消滅など、多くの興味深い動的挙動をもたらしましたが、これらはまだ根本的に解明されていません。理解と最終的な予測。しかし、CCA の化学的複雑さは、拡散媒介プロセスのモデリングに新たな課題をもたらします。

機械学習手法の出現により、非線形相互作用や大規模な組み合わせ空間を含む材料科学における複雑な計算問題を解決できる可能性が実証されました。

複雑な組成の合金における空孔の拡散に関して、重要な鍵となるパラメーターは、遷移状態と初期エネルギー最小値の間のエネルギー差である拡散エネルギー障壁 ΔE です。 CCA には原子スケールの組成変動と複数の拡散方向が存在するため、ベクトル特性、特に拡散経路関連のポテンシャル障壁を正確に予測するには機械学習モデルが必要です。

ニューラル ネットワーク ダイナミクス スキーム

この研究では、研究者らは、複雑で濃縮された化学環境における拡散誘起の化学進化と構造進化を予測およびシミュレーションするためのニューラル ネットワーク ダイナミクス (NNK) スキームを提案しました。

下の図は、空孔を含む初期原子配置が数値行列またはニューロン図にエンコードされた格子構造と化学表現です。数字 (1、2、および 3) は対応する原子の種類を表し、0 は空孔を表します。これらのベクトル化された数値は NNK モデルに渡され、入力ニューロンとして使用されます。

図: ニューラル ネットワーク ダイナミクス (NNK) フレームワークの概略図。 (出典: 論文)

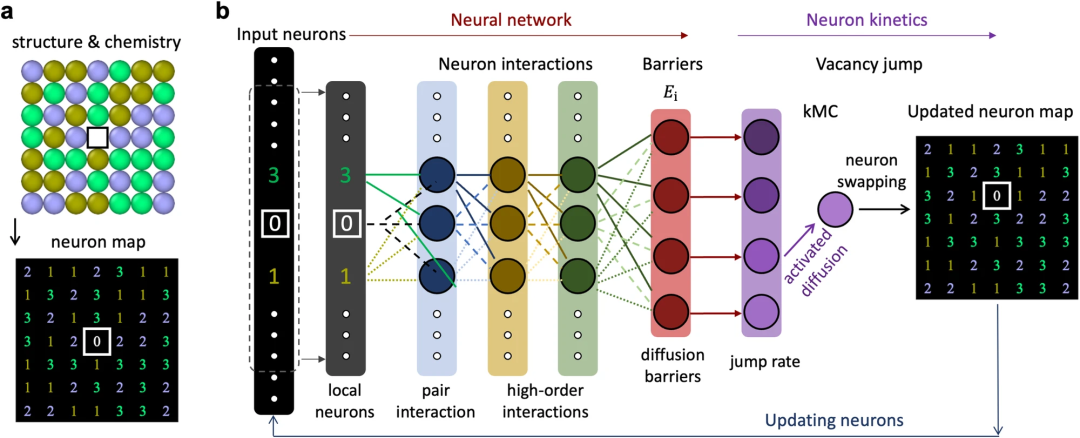
NNK は人工ニューラルネットワークとニューロンダイナミクスモジュールで構成されています。導入されたニューラル ネットワーク (2 つ以上の隠れ層を持つ) は、入力ニューロン (つまり、原子と空孔) と出力拡散エネルギー障壁の間の非線形相互作用を学習することを目的としています。特に、このネットワークは空孔とその隣接ニューロンのみを入力として使用するため、精度を犠牲にすることなく、低い一定の計算コストが得られます。

ニューロンダイナミクスモジュールは、動的モンテカルロ法を使用して、各拡散経路に関連付けられた利用可能なポテンシャル障壁を使用して拡散ダイナミクスを進化させます。原子配置をニューロン グラフに 1 回変換するだけで、ニューロン グラフの 2 桁を交換することで空孔ホッピングと化学進化をシミュレートできます。このようにして、各ジャンプの反復に 2 つのニューロンのみの動作が関与する、何百万ものギャップ ジャンプを効率的にモデル化できます。

複雑な組成の材料における拡散、化学秩序の探索

研究者らは、NNK と bcc NbMoTa をモデル系として使用して、拡散動力学を介した化学秩序と B2 相の形成を探索し、CCA (拡散多重度) の固有の異常拡散を明らかにしました。 。

B2 (B2 単位胞は、立方体の隅または中心に配列された Ta と Mo の 2 つの物質からなる単純な bcc 構造を持っています) の秩序が最大に達する臨界温度の存在を発見しました。化学的秩序の温度依存性は、基礎となる格子ホッピングの確率論と密接に関係しています。

図: 等モル NbMoTa 合金のホッピングランダム性と拡散多重度。 (出典: 論文)

融点に近い高温では、拡散ジャンプは最終的に純粋にランダムなプロセスに近づき、これは秩序形成の傾向が低いことに対応します。低温では、格子拡散は最も低い障壁経路によって支配され、方向性ホッピングとして現れ、化学的に規則正しい構造の核生成を制限します。中間範囲の臨界温度では、ランダムで方向性のある格子ホッピングがシステム全体に広がり、最も高い拡散不均一性 (多重度) を示します。

図: NbMoTa アニーリング中の B2 構造の核生成と成長の速度論。 (出典: 論文)

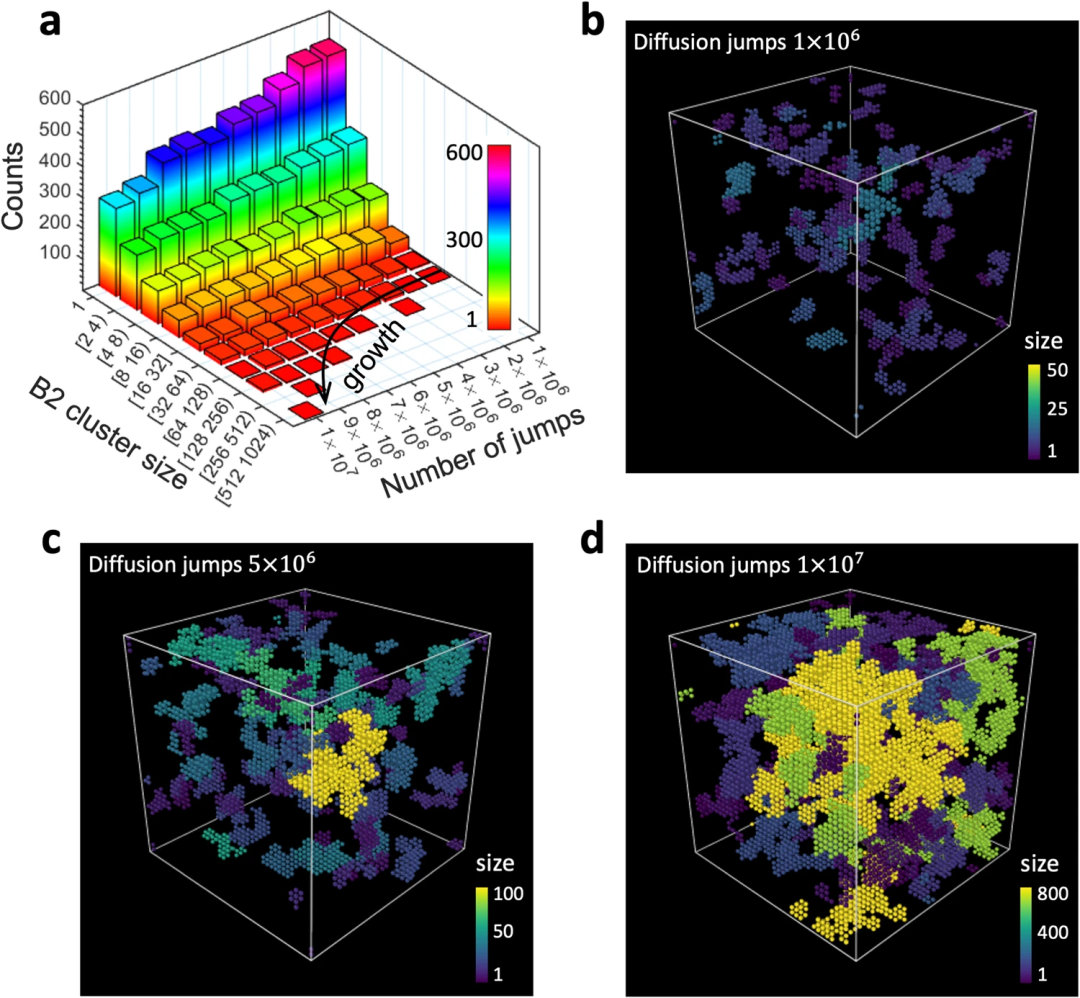
アニーリングプロセス中に個々のB2クラスターを追跡することにより、それらの核形成と成長が断続的で不均一であり、小さなクラスターの減少と消滅を伴うことが判明しました。 B2 構造の速度論的成長のこの際立った特徴は、より均一な成長を示すランダム原子タイプ交換を使用した仮想熱力学ベースのモデリングでは捕捉されませんでした。

これらの結果は、核生成、消滅、成長、秩序構造の再配列などの多くのプロセスが相互作用し調整する、安定状態に向かうCCAの複雑かつ多数の運動経路を強調しています。

図: Nb-Mo-Ta の組成空間全体にわたる拡散障壁スペクトルを予測します。 (出典: 論文)

数十のコンポーネントでトレーニングされたニューラル ネットワークは、目に見えないコンポーネントで高いパフォーマンスを示し、Nb-Mo-Ta の三元空間全体を明らかにします。組成のデザインスペースはほぼ無制限であるため、複数の要素を混合して形成された組成的に複雑なマテリアルは、探求すべき新しい領域を開きます。

多次元組成を拡散障壁スペクトルに直接リンクすることにより、NNK は、並外れた力学的特性が隠されている CCA の広大な組成空間の探索に向けた明るい道を示します。

以上が複合材料中の原子拡散を研究し、UC がニューラル ネットワーク ダイナミクス手法を開発の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。