Renversement après explosion ? KAN qui "a tué un MLP en une nuit" : En fait, je suis aussi un MLP

Le Perceptron multicouche (MLP), également connu sous le nom de réseau neuronal à réaction entièrement connecté, est l'élément de base des modèles d'apprentissage profond d'aujourd'hui. L'importance des MLP ne peut être surestimée, car ils constituent la méthode par défaut pour approximer les fonctions non linéaires dans l'apprentissage automatique.

Mais récemment, des chercheurs du MIT et d'autres institutions ont proposé une méthode alternative très prometteuse - KAN. Cette méthode surpasse le MLP en termes de précision et d’interprétabilité. De plus, il peut surpasser les MLP exécutés avec des tailles de paramètres beaucoup plus grandes et très peu de paramètres. Par exemple, les auteurs ont déclaré avoir utilisé KAN pour redécouvrir les lois mathématiques de la théorie des nœuds et reproduire les résultats de DeepMind avec des réseaux plus petits et un degré d'automatisation plus élevé. Plus précisément, le MLP de DeepMind compte environ 300 000 paramètres, tandis que le KAN n’en compte qu’environ 200.

Le contenu de mise au point est le suivant : Ces résultats de recherche étonnants ont rapidement rendu le KAN populaire et ont incité de nombreuses personnes à l’étudier. Bientôt, certains ont émis des doutes. Parmi eux, un document Colab intitulé « KAN is just MLP » est devenu le centre des discussions.

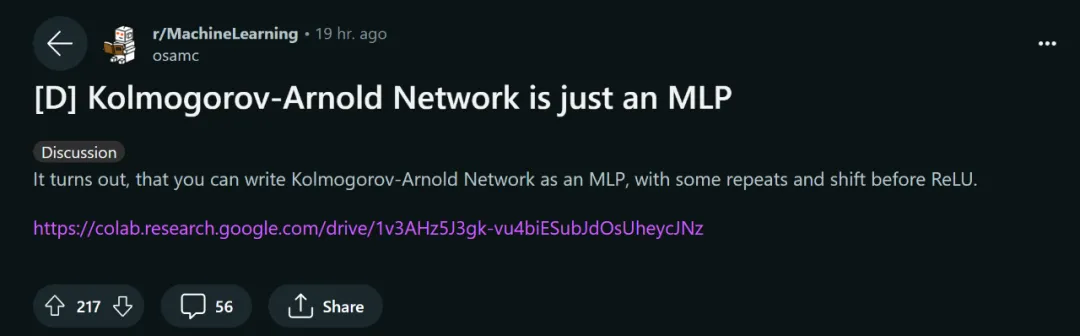
KAN Juste un MLP régulier ?

L'auteur du document ci-dessus a déclaré que vous pouvez écrire KAN en tant que MLP en ajoutant quelques répétitions et décalages avant ReLU.

Dans un court exemple, l'auteur montre comment réécrire le réseau KAN dans un MLP ordinaire avec le même nombre de paramètres et une structure légèrement non linéaire.

Ce qu'il faut retenir c'est que KAN dispose de fonctions d'activation sur les tranches. Ils utilisent des B-splines. Dans les exemples présentés, les auteurs n'utiliseront que des fonctions linéaires par morceaux pour plus de simplicité. Cela ne change pas les capacités de modélisation du réseau.

Voici un exemple de fonction linéaire par morceaux :

def f(x):if x 

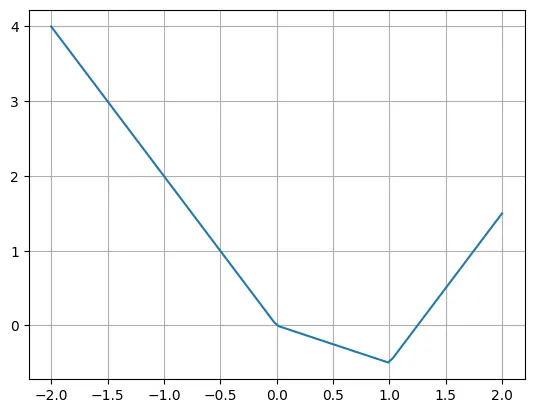
L'auteur a déclaré que nous pouvons facilement réécrire cette fonction en utilisant plusieurs fonctions ReLU et linéaires. Notez qu'il est parfois nécessaire de déplacer l'entrée de ReLU.

plt.plot(X, -2*X + torch.relu(X)*1.5 + torch.relu(X-1)*2.5)plt.grid()

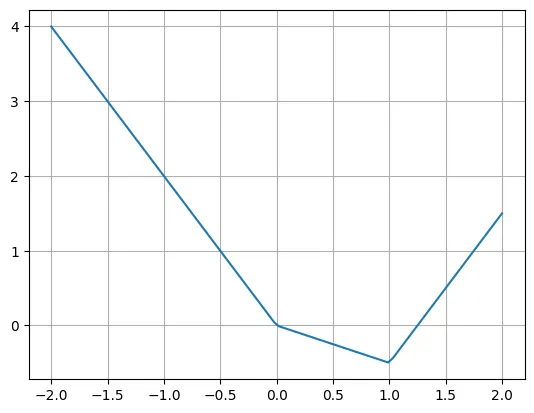
La vraie question est de savoir comment réécrire la couche KAN en une couche MLP typique. Supposons qu’il y ait n neurones d’entrée, m neurones de sortie et que la fonction par morceaux comporte k morceaux. Cela nécessite n*m*k paramètres (k paramètres par arête, et vous avez n*m ​​​​arêtes).

Considérons maintenant un bord KAN. Pour ce faire, l'entrée doit être copiée k fois, chaque copie décalée d'une constante, puis parcourue par ReLU et les couches linéaires (sauf la première couche). Graphiquement, cela ressemble à ceci (C est la constante et W est le poids) :

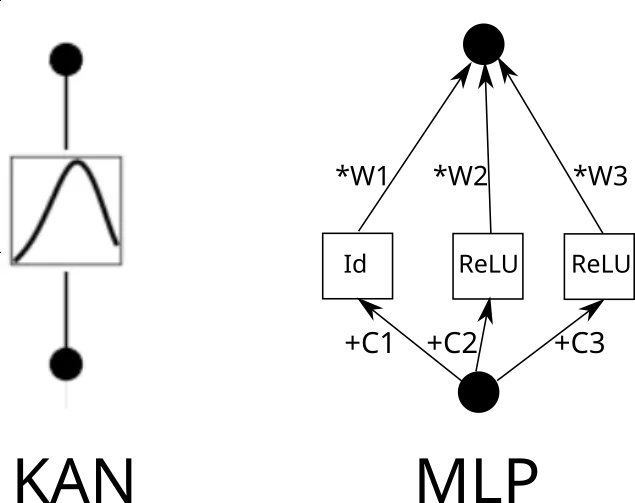
Maintenant, vous pouvez répéter ce processus pour chaque arête. Mais une chose à noter est que si la grille de fonctions linéaires par morceaux est la même partout, nous pouvons partager la sortie ReLU intermédiaire et simplement mélanger les poids dessus. Comme ceci :

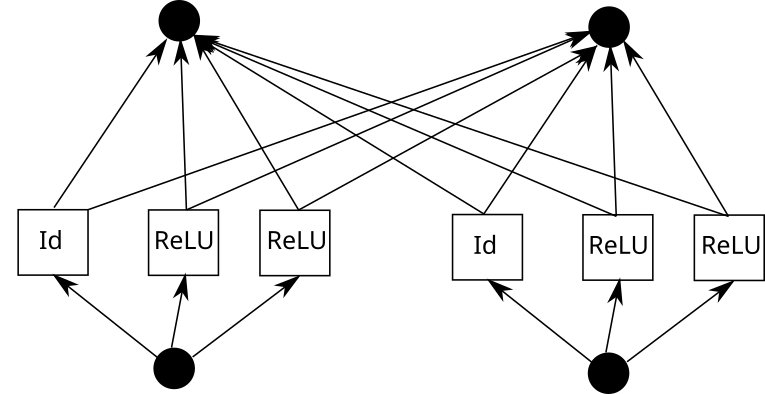
Dans Pytorch, cela se traduit par :

k = 3 # Grid sizeinp_size = 5out_size = 7batch_size = 10X = torch.randn(batch_size, inp_size) # Our inputlinear = nn.Linear(inp_size*k, out_size)# Weightsrepeated = X.unsqueeze(1).repeat(1,k,1)shifts = torch.linspace(-1, 1, k).reshape(1,k,1)shifted = repeated + shiftsintermediate = torch.cat([shifted[:,:1,:], torch.relu(shifted[:,1:,:])], dim=1).flatten(1)outputs = linear(intermediate)

Maintenant, nos calques ressemblent à ceci :

• Développer + décalage + ReLU
• Linéaire

Considérez les trois calques l'un après l'autre :

• Développer + décalage + ReLU (Couche 1 commence ici)
• Linéaire
• Développer + Maj + ReLU (La couche 2 commence ici)
• Linéaire
• Développer + Maj + ReLU (La couche 3 commence ici Commencer ici)
• Linéaire

En ignorant l'expansion des entrées, nous pouvons réorganiser :

• Linéaire (la couche 1 commence ici)
• Développer + décalage + ReLU
• Linéaire (la couche 2 commence ici)
• Développer + Maj + ReLU

La couche suivante peut essentiellement être appelée un MLP. Vous pouvez également agrandir la couche linéaire et supprimer l'expansion et le décalage pour obtenir de meilleures capacités de modélisation (bien qu'à un coût de paramètre plus élevé).

• Linéaire (La couche 2 commence ici)
• Expand + shift + ReLU

A travers cet exemple, l'auteur montre que KAN est une sorte de MLP. Cette affirmation a incité chacun à repenser les deux types de méthodes.

Réexamen des idées, des méthodes et des résultats de la KAN

En fait, outre la relation floue avec le MLP, la KAN a également été remise en question sous de nombreux autres aspects.

En résumé, la discussion des chercheurs a principalement porté sur les points suivants.

Premièrement, la principale contribution de KAN réside dans l'interprétabilité, pas dans la vitesse d'expansion, la précision, etc.

L'auteur de l'article a dit un jour :

1. KAN évolue plus rapidement que MLP. KAN a une meilleure précision que MLP avec moins de paramètres.
2. KAN peut être visualisé intuitivement. KAN offre une interprétabilité et une interactivité que MLP ne peut pas offrir. Nous pouvons potentiellement découvrir de nouvelles lois scientifiques en utilisant les KAN.

Parmi eux, l'importance de l'interprétabilité du réseau pour que le modèle résolve des problèmes réels est évidente :

Mais le problème est : "Je pense que leur affirmation est justement cela il apprend plus rapidement et a une interprétabilité, plutôt que quelque chose d'autre. Le premier a du sens si KAN a beaucoup moins de paramètres que l'équivalent NN. J'ai toujours l'impression que la formation de KAN est très instable. Alors, que peut-il faire exactement ? moins de paramètres que le NN équivalent ?

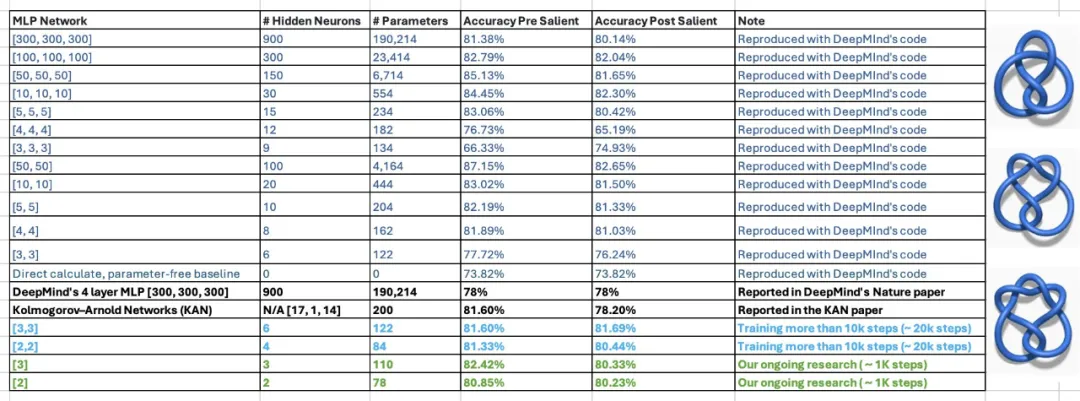
Cette affirmation est encore discutable. Dans l'article, les auteurs de KAN ont déclaré qu'ils étaient capables de reproduire les recherches de DeepMind sur les théorèmes mathématiques en utilisant un MLP de 300 000 paramètres en utilisant seulement 200 paramètres de KAN. Après avoir vu les résultats, deux étudiants du professeur agrégé de Georgia Tech, Humphrey Shi, ont réexaminé les expériences de DeepMind et ont découvert qu'avec seulement 122 paramètres, le MLP de DeepMind pouvait égaler la précision de 81,6 % de KAN. De plus, ils n’ont apporté aucune modification majeure au code DeepMind. Pour obtenir ce résultat, ils ont simplement réduit la taille du réseau, utilisé des graines aléatoires et augmenté le temps de formation.

En réponse, l'auteur de l'article a également donné une réponse positive :

Deuxièmement, KAN et MLP ne sont pas fondamentalement différents dans leur méthode.

"Ouais, c'est évidemment la même chose. Dans KAN, ils font d'abord l'activation puis la combinaison linéaire, alors qu'en MLP, ils font d'abord la combinaison linéaire puis l'activation. Amplifiez-le, en gros, c'est la même chose. Autant que je sache, les principales raisons d'utiliser KAN sont l'interprétabilité et la régression symbolique. " En plus de remettre en question la méthode, les chercheurs ont également demandé le retour de l'évaluation de cet article. Raison :

« Je pense que les gens Il faut arrêter de considérer l'article KAN comme un changement radical dans l'unité de base de l'apprentissage profond, et le considérer simplement comme un bon article sur l'interprétabilité de l'apprentissage profond. Apprendre à tous les niveaux. L'interprétabilité des fonctions non linéaires est la principale contribution de cet article. . "

Troisièmement, certains chercheurs ont déclaré que l'idée du KAN n'est pas nouvelle.

"Les gens étudiaient cela dans les années 1980. Une discussion de Hacker News mentionnait un journal italien discutant de ce problème. Ce n'est donc pas du tout nouveau. 40 ans plus tard, c'est juste quelque chose qui est revenu ou a été rejeté. et a été revisité."

Mais on voit que les auteurs de l'article de la KAN n'ont pas non plus passé sous silence la question.

« Ces idées ne sont pas nouvelles, mais je ne pense pas que l'auteur s'en détourne. Il a juste tout bien emballé et a fait de belles expériences sur les données des jouets. Mais c'est aussi une contribution. »

Dans le même temps, l'article MaxOut de Ian Goodfellow et Yoshua Bengio (https://arxiv.org/pdf/1302.4389) il y a plus de dix ans a également été mentionné. Certains chercheurs pensent que les deux « bien que légèrement Il existe des différences, mais le. les idées sont quelque peu similaires.

Auteur : L'objectif initial de la recherche était en effet l'interprétabilité

À la suite d'une discussion animée, l'un des auteurs, Sachin Vaidya, s'est manifesté.

En tant que l'un des auteurs de cet article, je voudrais dire quelques mots. L’attention que reçoit KAN est incroyable, et cette discussion est exactement ce qu’il faut pour pousser les nouvelles technologies à leurs limites et découvrir ce qui fonctionne et ce qui ne fonctionne pas.

J'ai pensé partager quelques informations sur la motivation. Notre idée principale pour la mise en œuvre de KAN découle de notre recherche de modèles d’IA interprétables capables « d’apprendre » les connaissances que les physiciens découvrent sur les lois naturelles. Par conséquent, comme d’autres l’ont réalisé, nous sommes entièrement concentrés sur cet objectif, car les modèles traditionnels de boîte noire ne peuvent pas fournir des informations essentielles aux découvertes scientifiques fondamentales. Nous montrons ensuite à travers des exemples liés à la physique et aux mathématiques que KAN surpasse significativement les méthodes traditionnelles en termes d'interprétabilité. Nous espérons certainement que l’utilité de KAN s’étendra bien au-delà de nos motivations initiales.

Sur la page d'accueil de GitHub, Liu Ziming, l'un des auteurs de l'article, a également répondu à l'évaluation de cette recherche :

La question la plus courante qu'on m'a posée récemment est de savoir si KAN deviendra la prochaine génération de LLM. Je n'ai pas de jugement clair à ce sujet.

KAN est conçu pour les applications soucieuses d'une grande précision et interprétabilité. Nous nous soucions de l'interprétabilité des LLM, mais l'interprétabilité peut signifier des choses très différentes pour les LLM et la science. Sommes-nous soucieux de la haute précision du LLM ? Les lois d'échelle semblent l'impliquer, mais peut-être pas de manière très précise. De plus, l’exactitude peut également signifier des choses différentes pour le LLM et la science.

J'invite les gens à critiquer KAN, la pratique est le seul critère pour tester la vérité. Il y a beaucoup de choses que nous ne savons pas à l’avance jusqu’à ce qu’elles soient réellement essayées et prouvées comme étant un succès ou un échec. Même si j'aimerais voir la KAN réussir, je suis tout aussi curieux de connaître son échec.

KAN et MLP ne se substituent pas l'un à l'autre. Ils présentent chacun des avantages dans certains cas et des limites dans certains cas. Je serais intéressé par des cadres théoriques qui englobent les deux, et peut-être même proposer de nouvelles alternatives (les physiciens adorent les théories unifiées, désolé).

KAN Le premier auteur de l'article est Liu Ziming. Il est physicien et chercheur en apprentissage automatique et est actuellement doctorant en troisième année au MIT et à l'IAIFI sous la direction de Max Tegmark. Ses intérêts de recherche portent sur l’intersection de l’intelligence artificielle et de la physique.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!