Identifier le surapprentissage et le sous-apprentissage grâce à des courbes d'apprentissage

Cet article expliquera comment identifier efficacement le surapprentissage et le sous-apprentissage dans les modèles d'apprentissage automatique grâce à des courbes d'apprentissage.

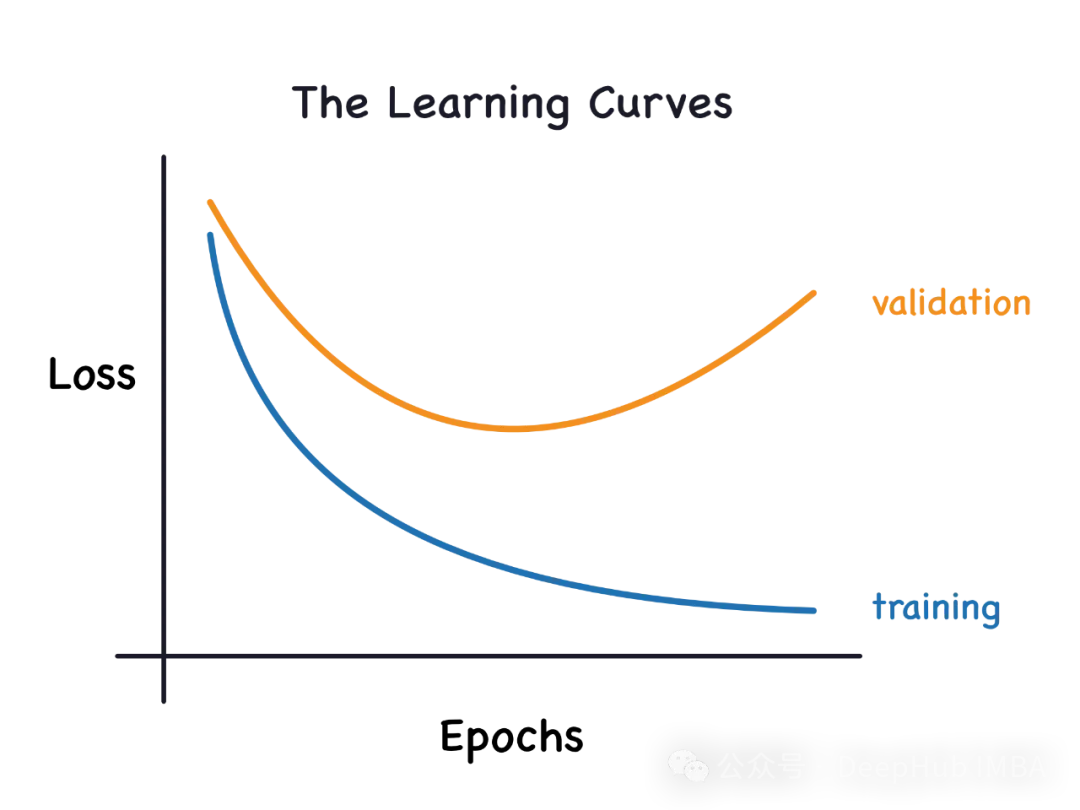
Sous-apprentissage et surapprentissage

1. Surapprentissage

Si un modèle est surentraîné sur les données afin qu'il en apprenne le bruit, alors le modèle est appelé surapprentissage. Un modèle surajusté apprend chaque exemple si parfaitement qu'il classera mal un exemple inédit/inédit. Pour un modèle surajusté, nous obtiendrons un score d'ensemble d'entraînement parfait/presque parfait et un score d'ensemble/test de validation épouvantable.

Légèrement modifié : "Cause du surajustement : l'utilisation d'un modèle complexe pour résoudre un problème simple extrait le bruit des données. Parce qu'un petit ensemble de données en tant qu'ensemble d'entraînement peut ne pas représenter une représentation correcte de toutes les données." 2. Sous-ajustement

Si un modèle ne peut pas apprendre correctement les modèles dans les données, nous disons qu'il est sous-ajusté. Les modèles de sous-ajustement n'apprennent pas pleinement tous les exemples de l'ensemble de données. Dans ce cas, nous constatons que les erreurs sur les ensembles de formation et de validation sont faibles. Cela peut être dû au fait que le modèle est trop simple et ne comporte pas suffisamment de paramètres pour s'adapter aux données. On peut essayer d'augmenter la complexité du modèle, d'augmenter le nombre de couches ou de neurones, pour résoudre le problème de sous-ajustement. Cependant, il convient de noter que la complexité croissante des modèles augmente également le risque de surajustement.

Raisons pour lesquelles cela ne convient pas : Utilisez un modèle simple pour résoudre un problème complexe. Le modèle ne peut pas apprendre tous les modèles des données, ou le modèle n'apprend pas correctement les modèles des données sous-jacentes. Dans l'analyse des données et l'apprentissage automatique, la sélection du modèle est très importante. Choisir le bon modèle pour votre problème peut améliorer la précision et la fiabilité de vos prédictions. Pour les problèmes complexes, des modèles plus complexes peuvent être nécessaires pour capturer tous les modèles présents dans les données. De plus, vous devez également prendre en compte la

Courbe d'apprentissage

La courbe d'apprentissage trace les pertes de formation et de validation de l'échantillon de formation lui-même en ajoutant progressivement de nouveaux échantillons de formation. Peut nous aider à déterminer si nous devons ajouter des exemples de formation supplémentaires pour améliorer le score de validation (score sur des données invisibles). Si le modèle est surajusté, l'ajout d'exemples de formation supplémentaires peut améliorer les performances du modèle sur des données invisibles. De même, si un modèle est sous-adapté, l’ajout d’exemples de formation peut ne pas être utile. La méthode 'learning_curve' peut être importée depuis le module 'model_selection' de Scikit-Learn.

from sklearn.model_selection import learning_curve

Nous ferons une démonstration en utilisant la régression logistique et les données Iris. Créez une fonction appelée « learn_curve » qui s'adaptera à un modèle de régression logistique et renverra les scores de validation croisée, les scores d'entraînement et les données de courbe d'apprentissage.

#The function below builds the model and returns cross validation scores, train score and learning curve data def learn_curve(X,y,c): ''' param X: Matrix of input featuresparam y: Vector of Target/Labelc: Inverse Regularization variable to control overfitting (high value causes overfitting, low value causes underfitting)''' '''We aren't splitting the data into train and test because we will use StratifiedKFoldCV.KFold CV is a preferred method compared to hold out CV, since the model is tested on all the examples.Hold out CV is preferred when the model takes too long to train and we have a huge test set that truly represents the universe'''  le = LabelEncoder() # Label encoding the target sc = StandardScaler() # Scaling the input features y = le.fit_transform(y)#Label Encoding the target log_reg = LogisticRegression(max_iter=200,random_state=11,C=c) # LogisticRegression model # Pipeline with scaling and classification as steps, must use a pipelne since we are using KFoldCV lr = Pipeline(steps=(['scaler',sc],['classifier',log_reg]))   cv = StratifiedKFold(n_splits=5,random_state=11,shuffle=True) # Creating a StratifiedKFold object with 5 folds cv_scores = cross_val_score(lr,X,y,scoring="accuracy",cv=cv) # Storing the CV scores (accuracy) of each fold   lr.fit(X,y) # Fitting the model  train_score = lr.score(X,y) # Scoring the model on train set  #Building the learning curve train_size,train_scores,test_scores =learning_curve(estimator=lr,X=X,y=y,cv=cv,scoring="accuracy",random_state=11) train_scores = 1-np.mean(train_scores,axis=1)#converting the accuracy score to misclassification rate test_scores = 1-np.mean(test_scores,axis=1)#converting the accuracy score to misclassification rate lc =pd.DataFrame({"Training_size":train_size,"Training_loss":train_scores,"Validation_loss":test_scores}).melt(id_vars="Training_size") return {"cv_scores":cv_scores,"train_score":train_score,"learning_curve":lc}

Le code ci-dessus est très simple, c'est notre processus de formation quotidien. Nous commençons maintenant à introduire l'utilisation de la courbe d'apprentissage

1. Fonction 'learn_curve' Un bon modèle d'ajustement est obtenu en définissant la variable/paramètre d'anti-régularisation 'c' sur 1 (c'est-à-dire que nous n'effectuons aucune régularisation).

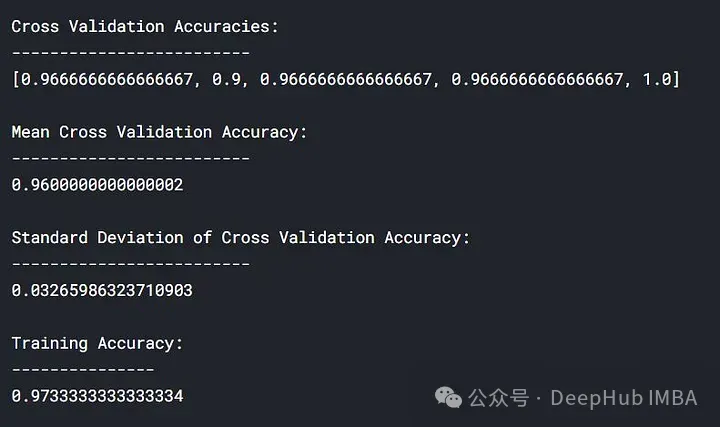
lc = learn_curve(X,y,1) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Deep HUB Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])}\n\n\ Training Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of Good Fit Model") plt.ylabel("Misclassification Rate/Loss");

Dans les résultats ci-dessus, la précision de la validation croisée est proche de la précision de l'entraînement.

Perte d'entraînement (bleu) : la courbe d'apprentissage d'un modèle bien ajusté diminuera et s'aplatira progressivement à mesure que le nombre d'exemples d'entraînement augmente, indiquant que l'ajout d'exemples d'entraînement supplémentaires ne pourra pas améliorer les performances du modèle sur les données d’entraînement.

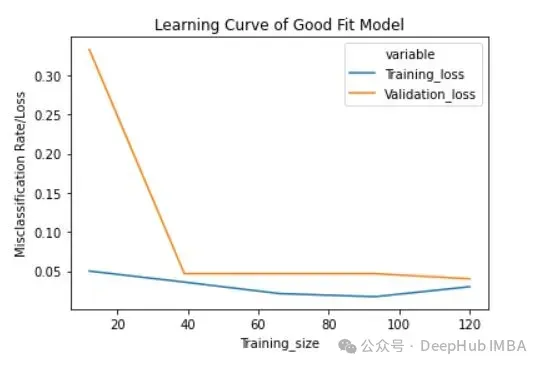Perte de validation (jaune) : la courbe d'apprentissage d'un modèle bien ajusté présente une perte de validation élevée au début, qui diminue progressivement et s'aplatit à mesure que le nombre d'échantillons d'entraînement augmente, indiquant que plus il y a d'échantillons, plus vous peut apprendre plus de modèles, ce qui sera utile pour les données "invisibles"

Enfin, vous pouvez également voir qu'après avoir ajouté un nombre raisonnable d'exemples de formation, la perte de formation et la perte de validation sont proches l'une de l'autre .

2. Courbe d'apprentissage du modèle de surajustement

Nous utiliserons la fonction 'learn_curve' pour obtenir la valeur élevée du modèle de surajustement (la valeur 'c' conduit au surajustement).

lc = learn_curve(X,y,10000) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Deep HUB Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])} (High Variance)\n\n\ Training Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of an Overfit Model") plt.ylabel("Misclassification Rate/Loss");

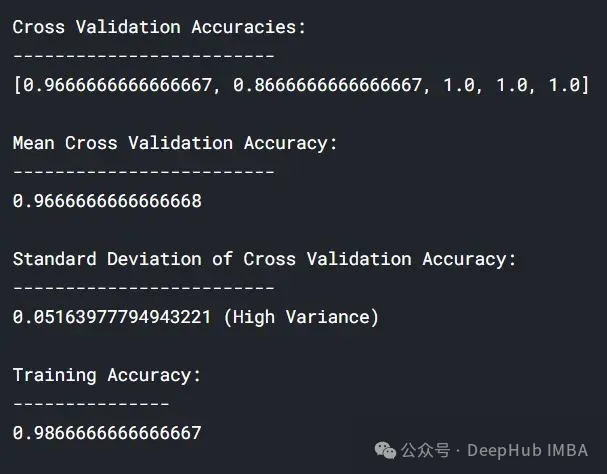
与拟合模型相比，交叉验证精度的标准差较高。

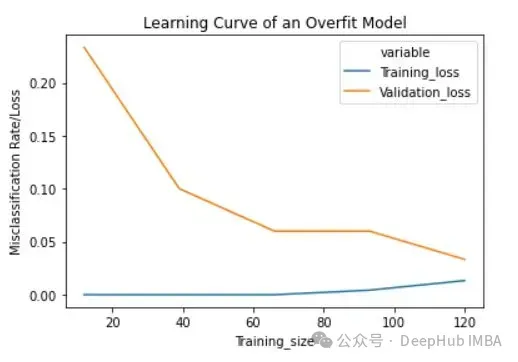
过拟合模型的学习曲线一开始的训练损失很低，随着训练样例的增加，学习曲线逐渐增加，但不会变平。过拟合模型的学习曲线在开始时具有较高的验证损失，随着训练样例的增加逐渐减小并且不趋于平坦，说明增加更多的训练样例可以提高模型在未知数据上的性能。同时还可以看到，训练损失和验证损失彼此相差很远，在增加额外的训练数据时，它们可能会彼此接近。

3、欠拟合模型的学习曲线

将反正则化变量/参数' c '设置为1/10000来获得欠拟合模型(' c '的低值导致欠拟合)。

lc = learn_curve(X,y,1/10000) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])} (Low variance)\n\n\ Training Deep HUB Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of an Underfit Model") plt.ylabel("Misclassification Rate/Loss");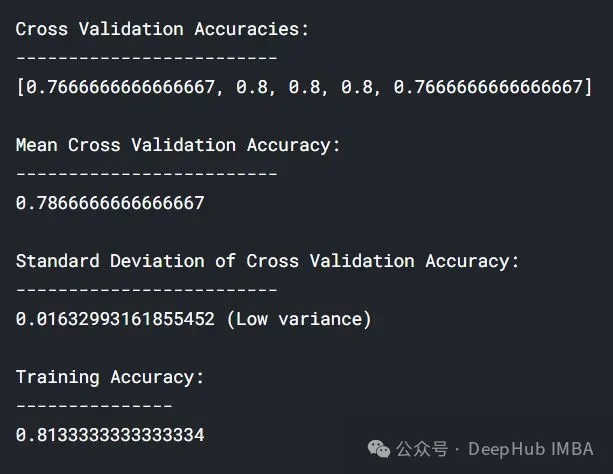

与过拟合和良好拟合模型相比，交叉验证精度的标准差较低。

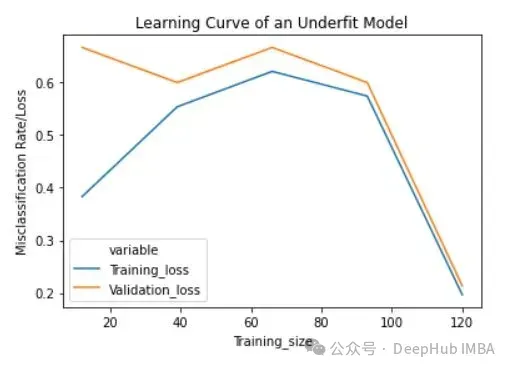
欠拟合模型的学习曲线在开始时具有较低的训练损失，随着训练样例的增加逐渐增加，并在最后突然下降到任意最小点(最小并不意味着零损失)。这种最后的突然下跌可能并不总是会发生。这表明增加更多的训练样例并不能提高模型在未知数据上的性能。

总结

在机器学习和统计建模中，过拟合（Overfitting）和欠拟合（Underfitting）是两种常见的问题，它们描述了模型与训练数据的拟合程度如何影响模型在新数据上的表现。

分析生成的学习曲线时，可以关注以下几个方面：

• 欠拟合：如果学习曲线显示训练集和验证集的性能都比较低，或者两者都随着训练样本数量的增加而缓慢提升，这通常表明模型欠拟合。这种情况下，模型可能太简单，无法捕捉数据中的基本模式。
• 过拟合：如果训练集的性能随着样本数量的增加而提高，而验证集的性能在一定点后开始下降或停滞不前，这通常表示模型过拟合。在这种情况下，模型可能太复杂，过度适应了训练数据中的噪声而非潜在的数据模式。

根据学习曲线的分析，你可以采取以下策略进行调整：

• 对于欠拟合：

• 增加模型复杂度，例如使用更多的特征、更深的网络或更多的参数。
• 改善特征工程，尝试不同的特征组合或转换。
• 增加迭代次数或调整学习率。

• 对于过拟合：

• 使用正则化技术（如L1、L2正则化）。

• 减少模型的复杂性，比如减少参数数量、层数或特征数量。

• 增加更多的训练数据。

• 应用数据增强技术。

• 使用早停（early stopping）等技术来避免过度训练。

通过这样的分析和调整，学习曲线能够帮助你更有效地优化模型，并提高其在未知数据上的泛化能力。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!