Augmentez vos connaissances! Apprentissage automatique avec des règles logiques

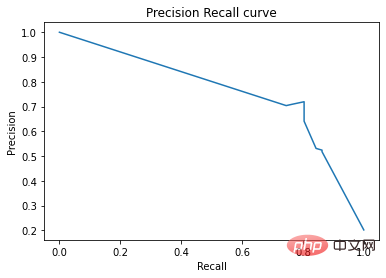
Sur la courbe précision-rappel, les mêmes points sont tracés avec des axes différents. Attention : Le premier point rouge à gauche (0% de rappel, 100% de précision) correspond à 0 règle. Le deuxième point à gauche est la première règle, et ainsi de suite.

Skope-rules utilise un modèle d'arborescence pour générer des règles candidates. Créez d’abord des arbres de décision et considérez les chemins allant du nœud racine aux nœuds internes ou aux nœuds feuilles comme candidats aux règles. Ces règles candidates sont ensuite filtrées selon certains critères prédéfinis tels que la précision et le rappel. Seuls ceux dont la précision et le rappel sont supérieurs à leurs seuils sont retenus. Enfin, un filtrage de similarité est appliqué pour sélectionner des règles présentant une diversité suffisante. En général, les règles Skope sont appliquées pour apprendre les règles sous-jacentes à chaque cause fondamentale.

Adresse du projet : https://github.com/scikit-learn-contrib/skope-rules

• Skope-rules est un module d'apprentissage automatique Python construit sur scikit-learn, sous BSD à 3 clauses Publié avec autorisation.
• Skope-rules vise à apprendre des règles logiques et interprétables pour "définir" la catégorie cible, c'est-à-dire détecter les instances de cette catégorie avec une grande précision.
• Les règles Skope sont un compromis entre l'interprétabilité des arbres de décision et les capacités de modélisation des forêts aléatoires.

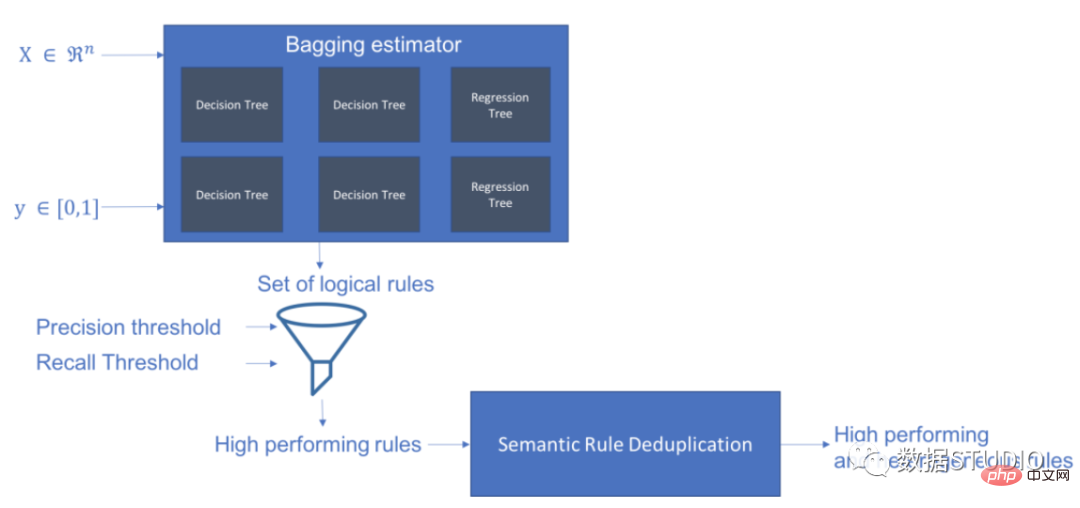
schema

Installation

Vous pouvez utiliser pip pour obtenir les dernières ressources :

pip install skope-rules

Démarrage rapide

SkopeRules peut être utilisé pour décrire des classes avec des règles logiques :

from skle arn .datasets import load_iri s UFrom Skrules Import Skoperules

dataset = load_iris ()
feature_names = ['SEPAL_LENGTH', 'SEPAL_WIDTH', 'Petal_length'] KClf = Skoperules (MAX_DEPTH_DUPLICATINOTALOW = 2,
n_estimators = 30, précision_min = 0,3 ,
rappel_min=0.1,
feature_names=feature_names)

pour idx, espèces dans enumerate(dataset.target_names) :
X, y = dataset.data, dataset.target
clf.fit(X, y == idx)
règles = clf.rules_[0:3]
print("Règles pour l'iris", espèce)
pour la règle dans les règles :
print(rule)
print()
print(20*'=')
print()

Remarque :

Si l'erreur suivante se produit :

Solution :

À propos de l'erreur d'importation Python : impossible d'importer le nom 'six' depuis 'sklearn.externals', Yun Duojun en a trouvé une similaire sur la question Stack Overflow : https://stackoverflow.com/questions/61867945/

La solution est la suivante

import six

import sys

sys.modules['sklearn.externals.six'] = six

import mlrose

Le test personnel est valide !
SkopeRules peut également être utilisé comme prédicteurs si vous utilisez la méthode "score_top_rules":

from sklearn.datasets import load_boston

from sklearn.metrics import précision_recall_curve

from matplotlib import pyplot as plt

from skrules import SkopeRules

dataset = pierre( )
clf = SkopeRules(max_degree_duplicatinotallow=Aucun,
n_estimators=30,
précision_min=0.2,
rappel_min=0.01,
feature_names=dataset.feature_names)

X, y = dataset.data, dataset.target > , y_train = X[:len(y)//2], y[:len(y)//2]
X_test, y_test = X[len(y)//2:], y[len(y)/ /2:]
clf.fit(X_train, y_train)
y_score = clf.score_top_rules(X_test) # Obtenez un score de risque pour chaque exemple de test
precision, rappel, _ = précision_recall_curve(y_test, y_score)
plt.plot(recall , précision)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision Recall curve')
plt.show()



Cas pratique

Cet étui présente Utilisation de règles de portée sur le célèbre ensemble de données Titanic.

situation applicable aux règles skope :

• Résoudre le problème de classification binaire
• Extraire des règles de décision interprétables

Ce cas est divisé en 5 parties

• Importer des bibliothèques pertinentes
• Préparation des données
• Formation du modèle (en utilisant la méthode ScopeRules().score_top_rules())
• Explication des "Règles de survie" (en utilisant SkopeRules().rules_property).
• Analyse des performances (en utilisant la méthode SkopeRules.predict_top_rules()).

Importer des bibliothèques associées

# Importer des règles skope
à partir de skrules importer SkopeRules

# Importer des bibliothèques
importer des pandas au format pd
à partir de sklearn.ensemble importer GradientBoostingClassifier, RandomForestClassifier
à partir de sklearn.model_selection importer train_test_split
à partir de l'importation de sklearn.tree DecisionTreeClassifier
importer matplotlib.pyplot en tant que plt
depuis sklearn.metrics importer roc_curve, précision_recall_curve
depuis matplotlib importer cm
importer numpy en tant que np
depuis sklearn.metrics importer confusion_matrix
depuis IPython.display importer display

# Importer des données Titanic
data = pd.read_csv('../data/titanic-train.csv')

Préparation des données

# Supprimer les lignes avec l'âge manquant
data = data.query('Age == Age')
# Créer un encodage pour la variable Sexe Valeur
data['isFemale'] = (data['Sex'] == 'female') * 1
# Unvaried Embarked crée une valeur codée
data = pd.concat(
[data,
pd.get_dummies(data. loc [:,'Embarked'],
dummy_na=False,
prefix='Embarked',
prefix_sep='_')],
axis=1
)
# Supprimer les variables inutilisées
data = data.drop( ['Name ', 'Ticket', 'Cabine',
'PassengerId', 'Sex', 'Embarked'],
axis = 1)
# Créer des ensembles de formation et de test
X_train, X_test, y_train, y_test = train_test_split(
data. drop(['Survived'], axis=1),
data['Survived'],
test_size=0.25, random_state=42)
feature_names = X_train.columns

print('Les noms de colonnes sont : ' + ' '. join(feature_names.tolist())+'.')
print('La forme de l'ensemble d'entraînement est : ' + str(X_train.shape) + '.')

Les noms de colonnes sont : Pclass Age SibSp Parch Fare
isFemale Embarked_C Embarked_Q Embarked_S.
La forme de l'ensemble de formation est : (535, 9).

Formation du modèle

# Former un classificateur d'amélioration de gradient pour les tests de référence
gradient_boost_clf = GradientBoostingClassifier(random_state=42, n_estimators=30, max_degree = 5)
gradient_boost_clf .fit(X_train, y_train)

# Entraîner un classificateur de forêt aléatoire pour l'analyse comparative
random_forest_clf = RandomForestClassifier(random_state=42, n_estimators=30, max_degree = 5)
random_forest_clf.fit(X_train, y_train)

# Entraîner un arbre de décision classificateur pour l'analyse comparative
decision_tree_clf = DecisionTreeClassifier(random_state=42, max_degree = 5)
decision_tree_clf.fit(X_train, y_train)

# Former une classification skope-rules-boosting
skope_rules_clf = SkopeRules(feature_names=feature_names, 2, n_estimateurs =30,
rappel_min=0,05, précision_min=0,9,
max_samples=0,7,
max_degree_duplicatinotallow= 4, max_degree = 5)
skope_rules_clf.fit(X _train, y_train)


# Calculer le score de prédiction
gradient_boost_scoring = gradient_boost _clf.predict_proba( X_test)[:, 1]
random_forest_scoring = random_forest_clf.predict_proba(X_test)[:, 1]
decision_tree_scoring = décision_tree_clf.predict_proba(X_test )[:, 1]

skope_rules_scoring = skope_rules_clf.score_top_rules ( ")

# Imprimer ces règles

rules_explanations = [

"Femme de moins de 3 ans et de moins de 37 ans en première ou deuxième classe. "
"Femme âgée de 3 ans et plus voyageant en première ou deuxième classe et payant plus de 26 euros. "
"Femme qui voyage en première ou en deuxième classe et paie plus de 29 euros. "
"Femme de plus de 39 ans voyageant en première ou en deuxième classe. "
]
print('Les quatre "règles de survie du Titanic" les plus performantes sont les suivantes :/n')
pour i_rule, règle dans enumerate(skope_rules_clf.rules_[:4])
print(rule[ 0])
print('->'+rules_explanations[i_rule]+ 'n')

Utiliser SkopeRules pour créer 9 règles

Les 4 meilleures "Règles de survie du Titanic" sont les suivantes :
Âge et Pclass 0,5
-> Femmes de moins de 3 ans et de moins de 37 ans, en première ou deuxième classe

Âge > ;= 2,5 et isFemme > 0,5
-> Les femmes de plus de 3 ans voyageant en première ou en deuxième classe et payant plus de 26 euros.

Tarif > 29,356250762939453
et Pclass 0,5
->

Âge > 38,5 et Pclass et estFemme > 0,5
-> Les femmes de plus de 39 ans voyageant en première ou en deuxième classe.

def calculate_y_pred_from_query(X, règle):
score = np.zeros(X.shape[0])
X = X.reset_index(drop=True)
score[list(X.query(rule).index)] = 1
return(score)

def calculate_performances_from_y_pred(y_true, y_pred, index_name='default_index'):
df = pd.DataFrame(data=
{
'precision':[sum(y_true * y_pred)/sum(y_pred )],
'recall':[sum(y_true * y_pred)/sum(y_true)]
},
index=[index_name],
columns=['precision', 'recall']
)
return(df) " from_y_pred( y_test, y_test_pred, 'test_set')],
axis=0)

return(performances)


print('Précision = 0,96 signifie que 96% des personnes identifiées par la règle sont des survivants.')
print(' Rappel = 0,12 signifie que les survivants identifiés par la règle représentent 12% du total des survivants')

for i in range(4):
print('Rule '+str(i+1)+':')
display(compute_train_test_query_performances(X_train, y_train,
X_test, y_test,
skope_rules_clf.rules_[i][ 0])
)

Precision = 0,96 signifie que 96 % des personnes déterminées par les règles sont des survivants.
Recall = 0,12 signifie que les survivants identifiés par la règle représentent 12 % du total des survivants.





Tests de performances du modèle

def plot_titanic_scores(y_true, scores_with_line=[], scores_with_points=[],
labels_with_line=['Gradient Boosting', 'Random Forest', 'Decision Tree'],
labels_with_points=[ 'skope-rules']):
gradient = np.linspace(0, 1, 10)color_list = [ cm.tab10(x) pour x en dégradé]

fig, axes = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)

ax = axes[0]

n_line = 0pour i_score, score en enumerate(scores_with_line):

n_line = n_line + 1

fpr, tpr, _ = roc_curve(y_true, score)

ax.plot(fpr, tpr, linestyle='-.', c=color_list[i_score], lw=1, label=labels_with_line[i_score])

pour i_score, score en énumération( scores_with_points):
fpr, tpr, _ = roc_curve(y_true, score)
ax.scatter(fpr[:-1], tpr[:-1], c=color_list[n_line + i_score], s=10, label= labels_with_points[i_score])
ax.set_title("ROC", fnotallow=20)
ax.set_xlabel('Taux de faux positifs', fnotallow=18)
ax.set_ylabel('Taux de vrais positifs (rappel)', fnotallow=18 )
ax.legend(loc='lower center', fnotallow=8)

ax = axes[1]
n_line = 0
pour i_score, score en énumération(scores_with_line):
n_line = n_line + 1
précision, rappel , _ = précision_recall_curve(y_true, score)
ax.step(recall, précision, linestyle='-.', c=color_list[i_score], lw=1,where='post', label=labels_with_line[i_score])
pour i_score, score en enumerate(scores_with_points):
precision, rappel, _ = précision_recall_curve(y_true, score)
ax.scatter(recall, précision, c=color_list[n_line + i_score], s=10, label=labels_with_points[i_score ])
ax.set_title("Precision-Recall", fnotallow=20)
ax.set_xlabel('Rappel (taux positif réel)', fnotallow=18)
ax.set_ylabel('Precision', fnotallow=18)
ax .legend(loc='lower center', fnotallow=8)
plt.show()

plot_titanic_scores(y_test,
scores_with_line=[gradient_boost_scoring, random_forest_scoring, decision_tree_scoring],
scores_with_points=[skope_rules_scoring]
)




Sur la courbe ROC, chaque point rouge correspond au nombre de règles activées (issues de skope-rules). Par exemple, le point le plus bas est le point résultat d’une règle (la meilleure). Le deuxième point le plus bas est le point de résultat des 2 règles, et ainsi de suite.

Sur la courbe précision-rappel, les mêmes points sont tracés avec des axes différents. Attention : Le premier point rouge à gauche (0% de rappel, 100% de précision) correspond à 0 règle. Le deuxième point à gauche est la première règle, et ainsi de suite.

Certaines conclusions peuvent être tirées de cet exemple.

• les règles skope fonctionnent mieux que les arbres de décision.
• les règles de skope fonctionnent de la même manière que l'amélioration aléatoire de la forêt/du dégradé (dans cet exemple).
• L'utilisation de 4 règles permet d'obtenir de très bonnes performances (61 % de rappel, 94 % de précision) (dans cet exemple).

n_rule_chosen = 4
y_pred = skope_rules_clf.predict_top_rules(X_test, n_rule_chosen)

print('Les performances atteintes avec '+str(n_rule_chosen)+' les règles découvertes sont les suivantes :')
compute_performances_from_y_pred(y_test, _pred, ' test_set')

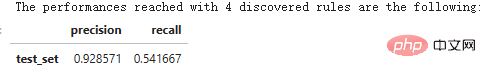
predict_top_rules(new_data, n_r) est utilisée pour calculer la prédiction de new_data, qui contient les premières règles de skope-rules n_r.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!