Maison >Périphériques technologiques >IA >Les Chinois de Caltech utilisent l'IA pour renverser les preuves mathématiques ! Accélérer 5 fois a choqué Tao Zhexuan, 80% des étapes mathématiques sont entièrement automatisées
Les Chinois de Caltech utilisent l'IA pour renverser les preuves mathématiques ! Accélérer 5 fois a choqué Tao Zhexuan, 80% des étapes mathématiques sont entièrement automatisées
- 王林avant
- 2024-04-23 15:01:29891parcourir
Lean Copilot, cet outil mathématique formel vanté par de nombreux mathématiciens comme Terence Tao, a encore évolué ?
Tout à l'heure, Anima Anandkumar, professeur à Caltech, a annoncé que l'équipe avait publié une version étendue du document Lean Copilot et mis à jour la base de code.
 Photos
Photos
Adresse papier : https://arxiv.org/pdf/2404.12534.pdf
Les dernières expériences montrent que cet outil Copilot peut automatiser plus de 80% des étapes de preuve mathématique ! Ce record est 2,3 fois meilleur que le précédent record d’Esope.
Et, comme avant, c'est open source sous licence MIT.
 Photos
Photos
C'est un Chinois Song Peiyang. Il est étudiant honoraire de premier cycle en CS à l'UCSB et chercheur SURF au département Informatique + Sciences mathématiques (CMS) du California Institute of Technology.
Les internautes se sont exclamés : Alors, la recherche mathématique de Tao Zhexuan peut désormais être accélérée 5 fois sur place ?
 Pictures
Pictures
LLM propose une stratégie de preuve, et les humains interviennent de manière transparente
L'équipe a publié cet outil Lean Copilot, dans l'espoir d'initier une collaboration entre les humains et LLM pour rédiger des preuves mathématiques formelles 100 % précises.
Il résout un défi technique majeur : exécuter l'inférence LLM dans Lean.
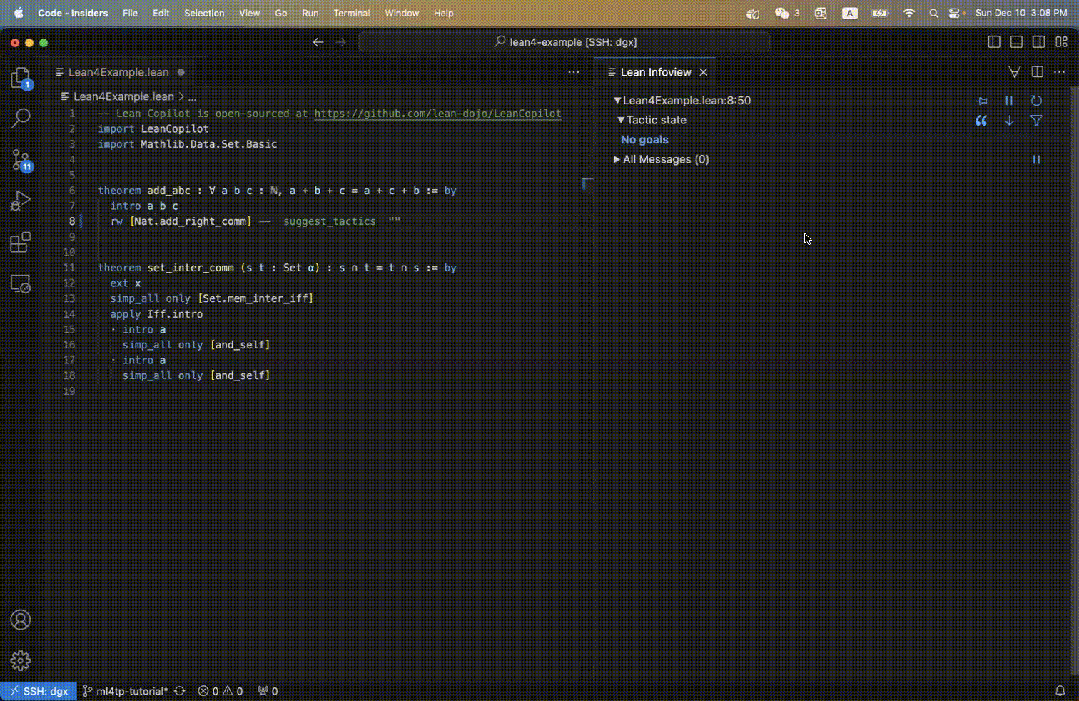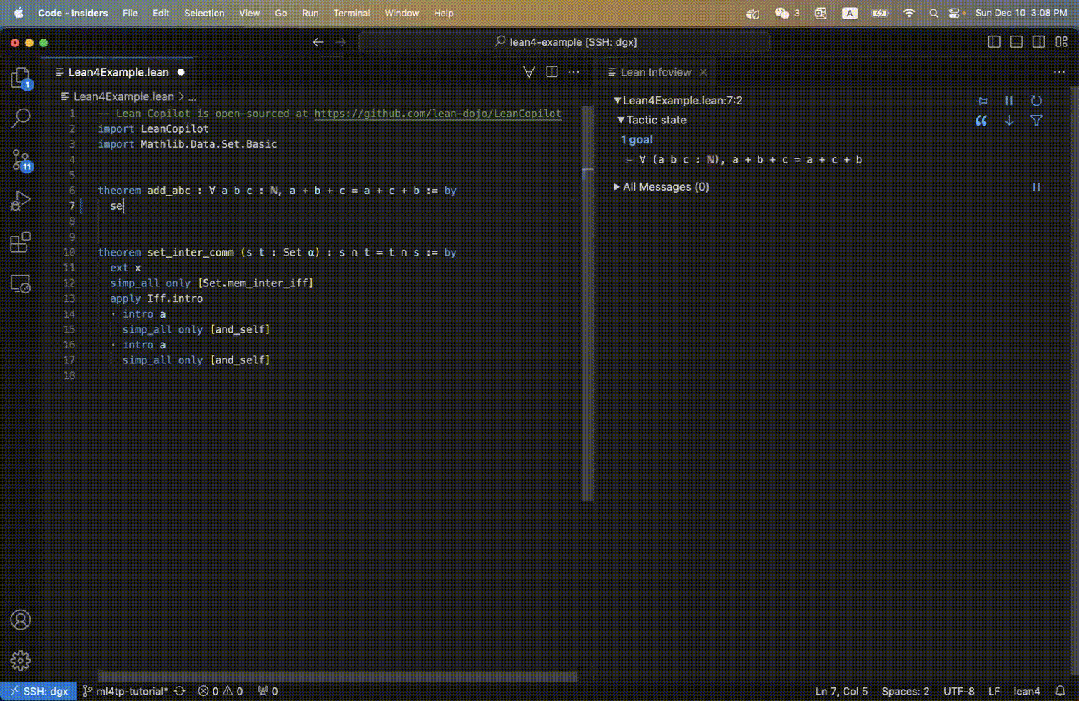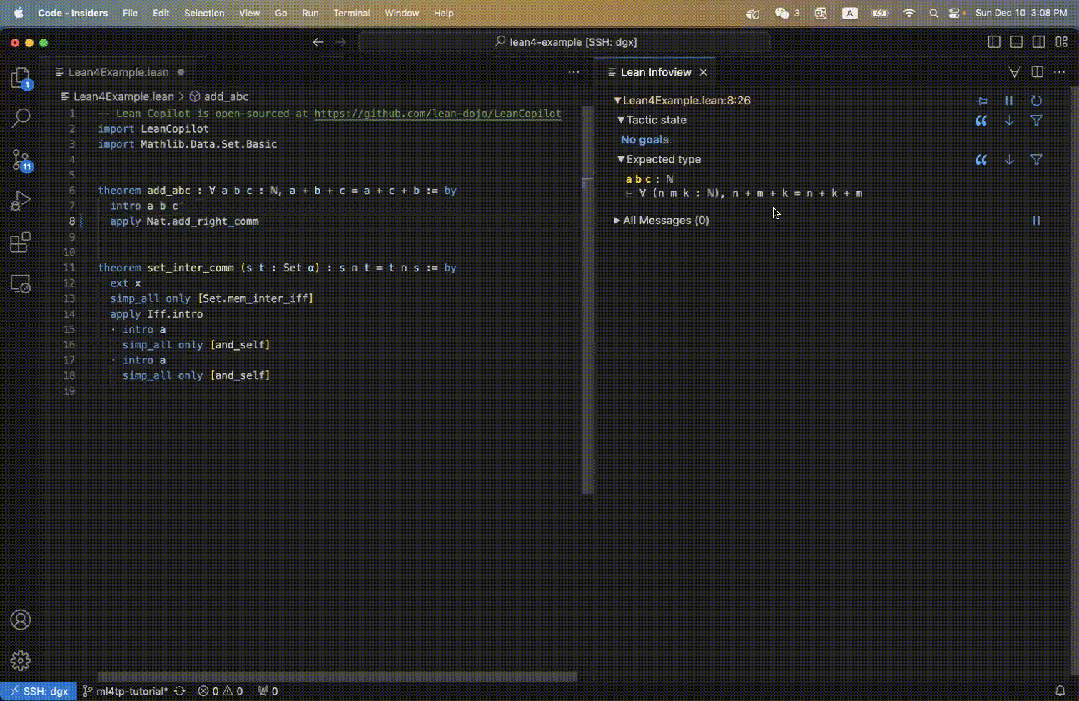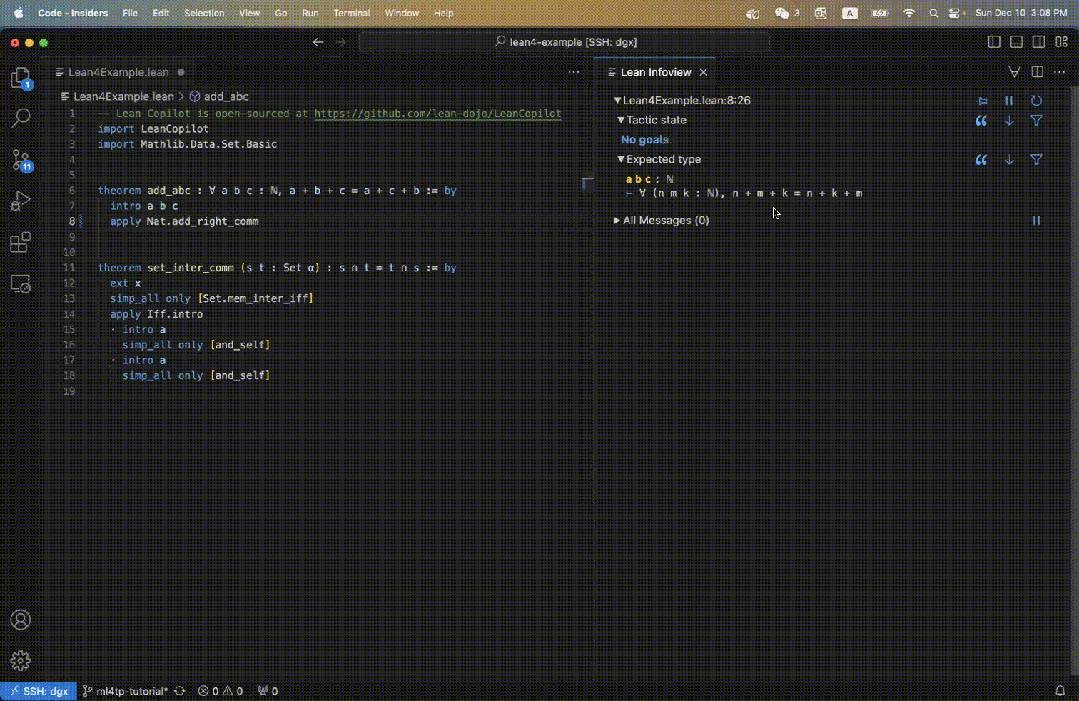
Grâce à cet outil, nous pouvons laisser LLM proposer des stratégies de preuve en Lean, permettant aux humains d'intervenir et de modifier de manière transparente.
 Pictures
Pictures
Ce projet a été développé parce que la démonstration automatisée de théorèmes est encore un défi difficile aujourd'hui.
Nous savons tous que LLM fait souvent des erreurs et des hallucinations lorsqu'il effectue des tâches de mathématiques et de raisonnement, et qu'il est très peu fiable.
 Photos
Photos
Jusqu'à présent, les preuves mathématiques ont été pour la plupart dérivées manuellement et nécessitent une vérification minutieuse.
Les outils de preuve de théorèmes comme Lean peuvent formaliser chaque étape du processus de preuve, mais il est vraiment laborieux pour les humains d'écrire Lean.
Dans ce cas, la naissance du Lean Copilot revêt une grande importance.
L'artefact qui a choqué Tao Zhexuan à plusieurs reprises : les mathématiciens ont fini avant de pouvoir l'utiliser
LLM peut être utilisé comme un outil pour aider les humains à prouver des théorèmes. Cet argument a été confirmé à plusieurs reprises par Tao Zhexuan.
Il vient de prédire dans son blog que dans 26 ans, l'IA sera combinée avec des outils de recherche et de mathématiques symboliques et deviendra un co-auteur digne de confiance dans la recherche mathématique.
Immédiatement après, des études pour étayer son point de vue ont poussé comme des champignons après une pluie.
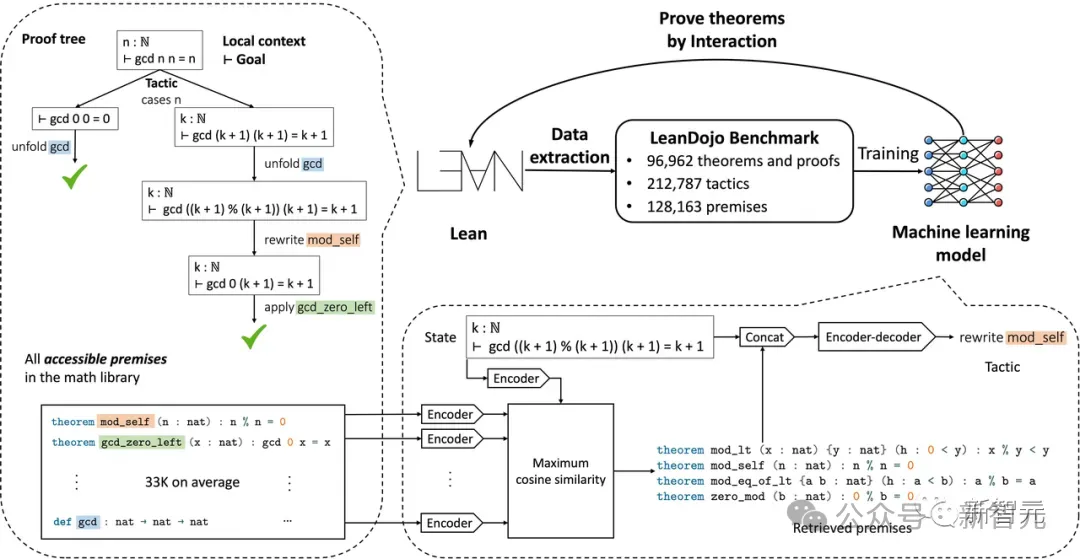
En juin de l'année dernière, des chercheurs du California Institute of Technology, de NVIDIA, du MIT et d'autres institutions ont construit LeanDojo, un prouveur de théorèmes basé sur un LLM open source.
 Photos
Photos
 Photos
Photos
Au 97ème cycle de dialogue, GPT-4 a conclu que l'exemple ne peut pas être résolu sans la méthode exhaustive, prouvant que la conclusion est P≠NP
En octobre dernier, Tao Zhexuan a directement découvert un bug caché dans son article avec l'aide de GPT-4 et Copilot.
En utilisant Lean4 pour formaliser l'argument de la page 6, il a découvert que l'expression
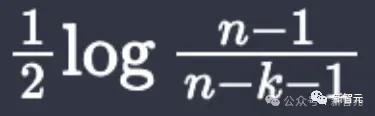 image
image
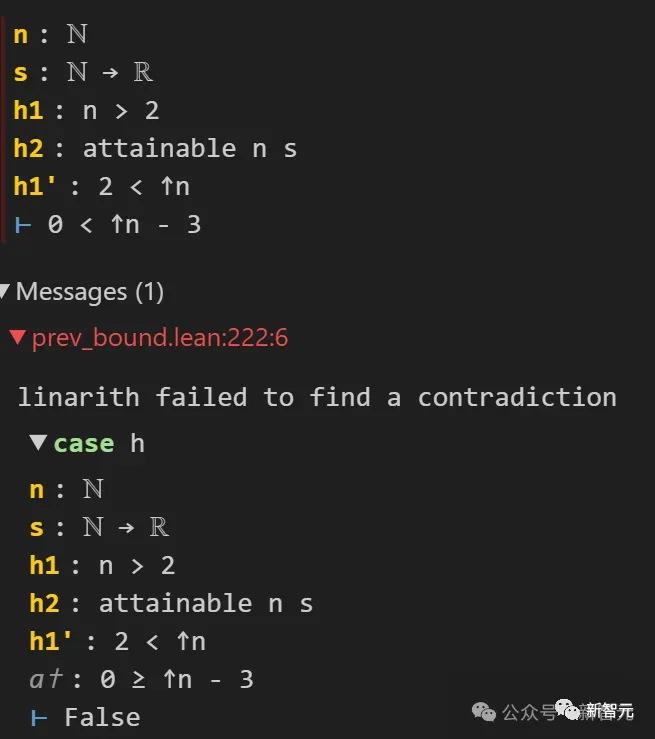
est en fait divergente lorsque n=3,k=2.
Ce bug difficile à voir a été détecté à temps, grâce à Lean4. La raison en est que Lean lui a demandé de construire 0
 Photos
Photos
Cette découverte a directement choqué les élèves de Tao Zhexuan.
 Photos
Photos
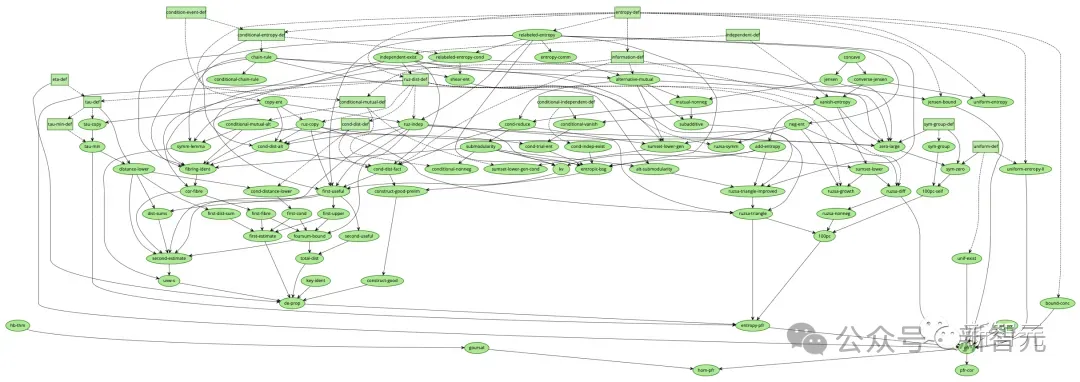
À la fin de l'année dernière, Tao Zhexuan a utilisé directement et avec succès les outils d'IA pour achever le travail de formalisation du processus de preuve de conjecture polynomiale de Freiman-Ruzsa.
 Picture
Picture
Enfin, le graphe de dépendances a été entièrement recouvert de vert, et le compilateur Lean rapporte également que cette conjecture suit pleinement les axiomes standards.
 Photos
Photos
Dans ce processus, tous les chercheurs en mathématiques de première ligne ont ressenti pour la première fois l'impact direct de l'IA sur le pouvoir subversif de la recherche mathématique.
Lean Copilot rend Lean meilleur à utiliser
Et aujourd'hui, cette recherche de Lean Copilot a rendu Lean directement plus puissant.
Dans cet article, l'équipe a construit des outils basés sur Lean Copilot pour suggérer des étapes de preuve (suggestion de stratégie), atteindre des objectifs de preuve intermédiaires (recherche de preuves) et sélectionner des locaux pertinents à l'aide de LLM (sélection de locaux).
Les résultats expérimentaux démontrent également pleinement que, par rapport à l'automatisation de la preuve basée sur des règles existante dans Lean, Lean Copilot est efficace pour aider les humains dans la preuve automatisée des théorèmes.
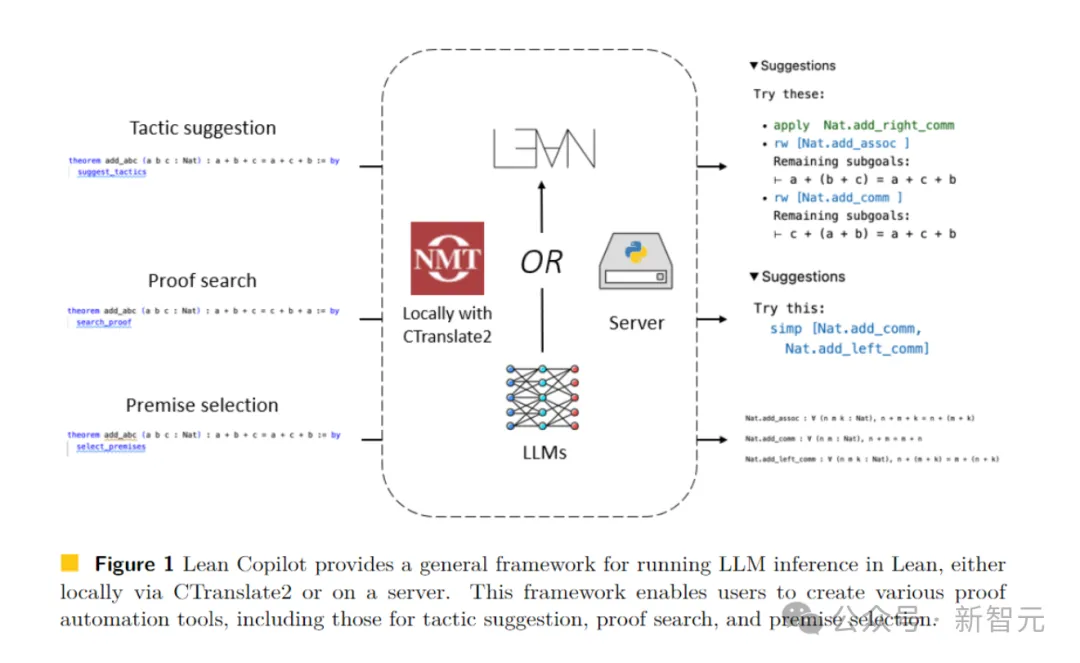
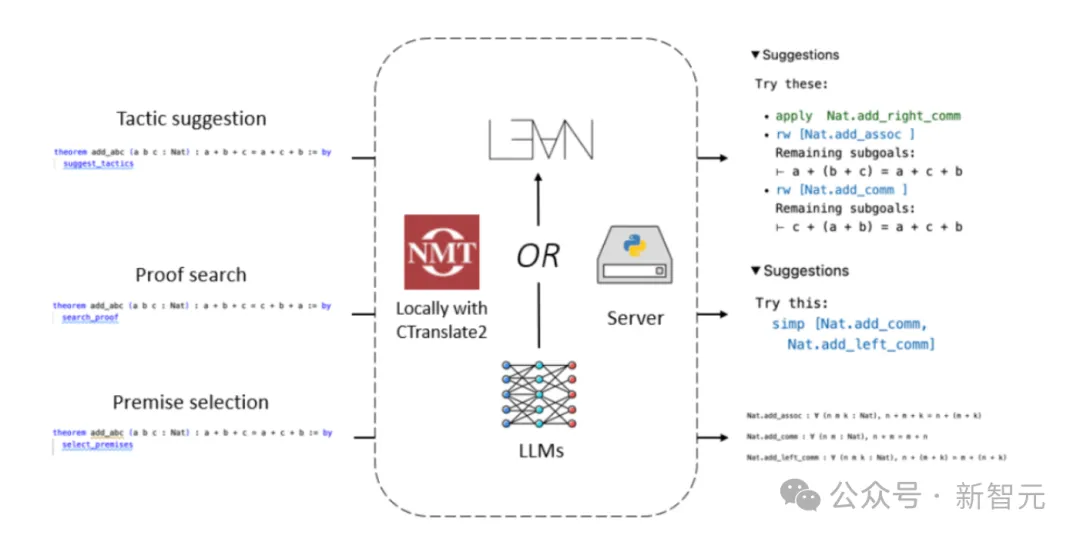
Lean Copilot fournit un cadre général qui peut exécuter l'inférence LLM localement via CTranslate 2 ou sur le serveur.
Grâce à ce framework, les utilisateurs peuvent créer divers outils de preuve automatisés.
 Pictures
Pictures
Lean est un assistant de preuve très populaire parmi les mathématiciens. Comme le montre la figure ci-dessous, une preuve en Lean consiste en une série d'étapes de preuve appelées tactiques.
 Images
Images
En partant du théorème entier comme objectif initial, la stratégie transforme de manière itérative l'objectif actuel en sous-objectifs plus simples jusqu'à ce que tous les objectifs soient résolus.
Les utilisateurs écrivent de manière interactive des stratégies dans l'EDI piloté par VSCode, et les objectifs sont affichés dans le panneau d'affichage d'informations sur la droite.
Générer des suggestions de stratégie
À l'aide de Lean Copilot, l'équipe a construit suggest_tropics, un outil permettant de générer des suggestions de stratégie à l'aide de LLM.
Et c'est aussi une stratégie en soi. Lorsque
est appliqué, il saisit la cible actuelle dans LLM et obtient la liste de candidats politiques générée par LLM.
Il examine chaque option pour voir si elles 1) entraînent une erreur ; 2) n'entraînent rien de mal mais ne parviennent pas à terminer la preuve ;
Si c'est 1), cette stratégie sera supprimée.
 Photos
Photos
Seules les stratégies sans erreur seront affichées dans le panneau d'affichage de droite.
Parmi elles, les stratégies qui réussissent la preuve sont marquées en vert (catégorie 3) ; les stratégies qui modifient l'objectif de la preuve sans erreur mais ne parviennent pas à terminer la preuve sont marquées en bleu (catégorie 2).
Attention ! Lorsque toutes les stratégies répertoriées entrent dans la catégorie 2, ces informations peuvent être extrêmement précieuses pour l'utilisateur.
Dans ce cas, les informations sur les objectifs restants peuvent directement aider l'utilisateur à choisir une stratégie comme prochaine étape de preuve intermédiaire.
Après avoir vu les suggestions, les utilisateurs peuvent choisir de les accepter ou de les utiliser comme source d'inspiration pour développer de nouvelles stratégies.
Par exemple, nous définissons un théorème add_abc dans le code Lean, et son objectif initial est indiqué sur le côté droit de la figure 3.
 Pictures
Pictures
Lorsque nous entrons dans suggest_tropics, nous verrons des suggestions de stratégie sur la droite.
La première stratégie est affichée en vert, indiquant que la preuve a été complétée avec succès.
Les trois suggestions suivantes sont toutes bleues, ce qui indique que la preuve ne peut pas être complétée directement, mais n'entraînera pas d'erreurs.
Ils sont donc susceptibles d'être des étapes de preuve intermédiaires valables !
Dans le même temps, les sous-objectifs restants sont également affichés.
Le champ État tactique affiche Aucun objectif car au moins une suggestion de stratégie peut être prouvée.
 Images
Images
Recherche de la preuve complète
De plus, comme ni les humains ni les machines ne peuvent produire systématiquement la bonne stratégie, le processus doit revenir en arrière et explorer différentes alternatives, ce qui est la recherche de preuves.
En ce qui concerne les Suggest_tropics mentionnés ci-dessus, il ne peut générer que la stratégie de l'étape en cours et n'a pas la capacité de rechercher des preuves multi-stratégies.
À cette fin, l'équipe l'a combiné avec l'outil de recherche de preuves basé sur des règles aesop pour créer un outil de recherche de preuves basé sur LLM.
Aesop mettra en œuvre la recherche « best-first » en tant que stratégie Lean et permettra aux utilisateurs de configurer la manière dont l'arborescence de recherche est développée.
 Images
Images
L'arbre de recherche est composé de cibles sous forme de nœuds.
Au départ, il n'a que la cible d'origine comme nœud racine. À chaque étape, Aesop sélectionne le nœud non développé le plus prometteur, le développe en appliquant une politique et ajoute le nœud résultant en tant que nœud enfant.
 Photos
Photos
Et lorsqu'Ésope trouve un chemin allant de la cause profonde à une cible facilement résoluble, cela prouve que la recherche est couronnée de succès !
Par conséquent, les performances d'Esope dépendent essentiellement de la configuration par l'utilisateur d'un ensemble de règles efficaces.
Cela montre qu'Esope manque de flexibilité. Par conséquent, Search_proof améliore l'ensemble de règles d'Esop en le rendant plus flexible avec les politiques liées aux cibles générées par suggest_tropics à chaque étape.
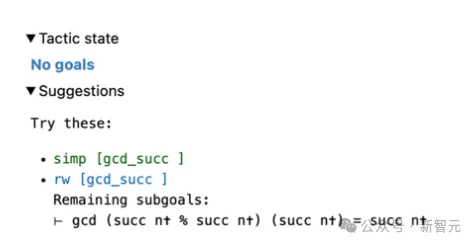
Pour l'objectif d'origine de la figure 3, l'utilisateur n'a qu'à saisir search_prrof et trouver une preuve complète qui peut résoudre l'objectif, qui est affichée dans la vue d'informations (Figure 5 à droite).
Vous pouvez voir que puisque des preuves de succès sont trouvées, l'état tactique restant est Aucun objectif.
 Images
Images
Choisissez des prémisses bien annotées
De plus, une autre tâche difficile et importante dans la preuve de théorème est de trouver des prémisses pertinentes qui réduisent ou complètent la preuve.
En plus d'un grand nombre de prérequis dans la bibliothèque de code source et la bibliothèque standard, Lean dispose également d'une grande bibliothèque mathématique (Mathlib).
Cependant, la recherche de locaux candidats dans toutes les bibliothèques est extrêmement difficile et prend beaucoup de temps.
Tant de personnes essaient d'obtenir l'aide du Lean ou d'autres assistants de preuve, ou d'automatiser ce processus.
 Photos
Photos
En Lean, la méthode de sélection de prémisses la plus avancée est un framework basé sur une forêt aléatoire (random forest) implémenté directement en Lean.
Cependant, la tâche de sélection des prémisses est bien adaptée au LLM amélioré par la récupération, où la matrice de récupération (intégration des prémisses) est entraînée lors de la formation d'un grand modèle pour estimer la corrélation entre la cible de preuve et les prémisses du candidat.
Étant donné un objectif de preuve au moment de l'inférence, codez d'abord l'objectif dans un vecteur, puis effectuez une multiplication matrice-vecteur entre l'intégration de prémisse et le vecteur objectif.
Ensuite, afin de sélectionner les k meilleurs locaux (où k peut être un hyperparamètre qui détermine le nombre de locaux que l'utilisateur souhaite retourner), il suffit de renvoyer les k locaux avec les scores les plus élevés.
Pour effectuer des tâches de raisonnement en Lean, en plus du raisonnement rapide fourni par Lean Copilot, vous avez également besoin d'une bibliothèque de multiplication matricielle efficace et d'un lecteur matriciel numpy C++.
Les chercheurs ont utilisé la fonction de multiplication matricielle de CTranslate2 et le lecteur de fichiers rapide numpy C++ de Libnpy.
Ils relient à nouveau ces chiffres au Lean via le mécanisme FFI.
Ainsi, la stratégie de sélection de prémisses peut fonctionner très efficacement, puisque les intégrations de prémisses peuvent être pré-calculées et que toutes les opérations ultérieures peuvent être effectuées rapidement en C++ à l'aide des bibliothèques présentées ci-dessus.
Après avoir obtenu la prémisse du retour, le chercheur l'a en outre annoté avec des informations utiles.
Tous les locaux sont répartis en deux catégories : les locaux directement utilisables dans l'environnement actuel (locaux hors périmètre) et les locaux non utilisables directement dans l'environnement actuel (locaux hors périmètre).
Cela dépend si les packages requis sont importés.
Vous pouvez facilement utiliser le local si vous avez déjà importé les packages requis par le local. La figure 6 ci-dessous montre une prémisse de portée annotée.

La figure 7 montre la prémisse annotée hors de portée.

Ce qui suit est un exemple d'utilisation de la "sélection de prémisses". Pour le théorème add_abc de la figure 3, vous pouvez saisir directement select_premises dans la preuve (figure 8 à gauche).
Ensuite, une liste de prérequis associés apparaîtra dans la vue d'informations (Figure 8, à droite).
Pour ce théorème simple, on voit clairement que les prémisses choisies sont effectivement pertinentes, car elles sont toutes liées aux nombres naturels et à la règle d'addition.
Dans ce cas, les 4 locaux sélectionnés sont tous dans le périmètre actuel, ce qui signifie que leurs modules sont déjà importés.

Ci-dessus sont trois outils pratiques d'automatisation des preuves construits par des chercheurs via Lean Copilot, qui sont utilisés pour les suggestions de stratégies, les preuves de recherche et la sélection des prémisses.
81,2 % des étapes de preuve sont toutes automatisées
Grâce au cadre Lean Copilot, les chercheurs avancent empiriquement l'hypothèse selon laquelle la collaboration homme-machine dans la preuve interactive du théorème Lean (ITP) est bénéfique.
En raison du processus de preuve de théorème dans Lean, il se concentre principalement sur la preuve de stratégie.
Par conséquent, dans l'expérience spécifique, l'auteur a principalement évalué les outils d'automatisation de preuves pour la « suggestion de stratégie » et la « recherche de preuves ».
En résumé, aesop est actuellement l'outil d'automatisation de preuves basé sur des règles le plus avancé pour la recherche de preuves.
Les chercheurs ont vérifié l'efficacité de la preuve de recherche basée sur LLM par rapport à Ésope dans deux cas :
(1) Preuve autonome du théorème (LLM complété indépendamment)
(2) Assistance aux humains pour exécuter le théorème prouver (les humains et l'IA collaborent)
De plus, les chercheurs ont également comparé les preuves de recherche avec des suggestions de stratégie pour prouver les avantages des preuves de recherche en plus des suggestions de stratégie uniques.
Étudiez comment Lean Copilot peut aider efficacement les humains dans le processus d'ITP, similaire au paradigme des humains utilisant Copilot dans la programmation logicielle.
C'est-à-dire que lorsque nous sommes confrontés à un objectif, nous appellerons d'abord Copilot pour voir s'il peut résoudre directement le problème.
Sinon, nous simplifions davantage l'objectif et essayons à nouveau Copilot. Ensuite, le processus ci-dessus est répété jusqu'à ce que Copilot résolve avec succès les cibles restantes.
Les chercheurs ont utilisé cet exemple de collaboration itérative pour voir combien de main d'œuvre chaque outil d'automatisation de preuve peut automatiser.
Les résultats spécifiques sont présentés dans le tableau 1 ci-dessous.
La recherche de preuves (search_proof) peut prouver automatiquement 64 % des théorèmes (32 sur 50), nettement plus élevé que les suggestions d'Ésope et de stratégie (suggest_tropics).
Lorsqu'elle est utilisée pour aider les humains, la recherche de preuves ne nécessite qu'une moyenne de 1,02 stratégies saisies manuellement, ce qui est également mieux qu'Ésope (3,62) et les suggestions de stratégies (2,72).
 Picture
Picture
Enfin, pour chaque théorème testé, les auteurs ont calculé le pourcentage d'étapes de preuve qui pourraient être automatisées par chacun des trois outils.
Les résultats ont révélé que la recherche de preuves peut effectuer automatiquement environ 81,2 % des étapes de preuve du théorème, ce qui est nettement supérieur aux suggestions de stratégie (48,6 %) et à Ésope (35,2 %).
En résumé, les performances de la recherche de preuves sont 1,67 fois supérieures à celles des suggestions politiques et 2,31 fois supérieures à celles de la ligne de base basée sur des règles d'Esope.
Inférence LLM native dans Lean via Copilot
suggestion tactique, recherche de preuves et sélection de prémisses dans Lean Copilot. Ces trois tâches peuvent sembler de nature différente, mais les exigences en matière d'expérience utilisateur sont similaires.
Ils doivent tous générer des réponses assez rapidement, avoir des exigences de calcul modérées, tout en fonctionnant en Lean.
La raison pour laquelle les utilisateurs ont ces exigences est que Lean lui-même peut fournir des commentaires sur l'environnement (tels que les cibles restantes, les messages d'erreur, les informations de type, etc.) très rapidement dans la plupart des cas.
Cette vitesse est cohérente avec l'essence de la démonstration du théorème : elle nécessite un raisonnement cohérent.
Si Lean Copilot oblige les utilisateurs à attendre longtemps, il sera difficile pour la collaboration entre les humains et l'IA de fonctionner.
De même, nous souhaitons également vraiment répondre aux besoins du low computing. Parce que la preuve de théorème dans Lean lui-même ne nécessite pas de GPU et peut être exécutée sur l'ordinateur portable local de l'utilisateur.
Par conséquent, il est très important que les utilisateurs Lean soient capables de fonctionner efficacement sur la plupart des matériels (y compris les ordinateurs portables sans GPU).
Parce que les utilisateurs peuvent ne pas avoir accès aux GPU compatibles CUDA lors de la rédaction de preuves.
Parce qu'une inférence rapide et de faibles exigences de calcul doivent être satisfaites, et que tous les frameworks d'apprentissage profond populaires et efficaces sont en Python, une solution naturelle à laquelle l'équipe a pensé était d'héberger le modèle en Python (local ou distant), et puis faites une requête au modèle depuis Lean.
Cependant, cette approche souffre de la surcharge de communication inter-processus, nécessite que les utilisateurs effectuent des étapes de configuration supplémentaires et n'est pas adaptée au flux de travail traditionnel de Lean.
Pour surmonter ces problèmes, Lean Copilot exécute LLM nativement dans Lean via l'interface de fonction étrangère (FFI).
FFI est un mécanisme qui permet à un programme écrit dans un langage d'appeler un sous-programme dans un autre langage.
La partie Lean est implémentée en c++ et peut interopérer efficacement avec c++.
Les programmeurs peuvent déclarer une fonction en Lean mais implémenter le corps de la fonction en C++. La mise en œuvre est compilée dans une bibliothèque partagée et liée dynamiquement au Lean.
Par défaut, nous utilisons le modèle de repver pré-entraîné LeanDojo. Il est basé sur un convertisseur codeur-décodeur, BVT5, qui mappe les chaînes d'entrée aux chaînes de sortie.
Lean Copilot le rend exécutable en Lean en encapsulant le modèle dans une fonction C++ qui opère sur des chaînes, qui peuvent être appelées en Lean via FFI.
 Photos
Photos
L'auteur chinois a apporté de grandes contributions
L'équipe de trois personnes du dernier article est également l'auteur de la plateforme open source LeanDojo le 23 juin.
 Photos
Photos
Adresse papier : https://arxiv.org/pdf/2306.15626.pdf
Peiyang Song (Song Peiyang)
 Photos
Photos
Chanson Peiyang est étudiant de premier cycle spécialisé en informatique au College of Creative Studies (CCS) de l'UC Santa Barbara, encadré par Richert Wang et Phill Conrad.
En parallèle, il est également chercheur SURF au Département des sciences informatiques et mathématiques (CMS) de Caltech, co-supervisé par le professeur Anima Anandkumar et le Dr Kaiyu Yang.
 Pictures
Pictures
De plus, il est chercheur au laboratoire d'architecture de l'UC Berkeley, en collaboration avec Tim Sherwood et le Dr Jeremy Lau (Google).
Ses intérêts de recherche sont l'apprentissage automatique (ML), impliquant des domaines d'application tels que le traitement du langage naturel (NLP) et la vision par ordinateur (CV), ainsi que les théories de base telles que les systèmes et les langages de programmation (PL).
Les recherches récentes de Song Peiyang ont principalement deux directions.
L'un d'entre eux est le raisonnement symbolique neuronal et les mathématiques de l'intelligence artificielle (AI4Math), qui combine de grands modèles avec des démonstrateurs de théorèmes interactifs (ITP).
L'autre est l'apprentissage automatique économe en énergie basé sur la logique temporelle.
Kaiyu Yang (杨凯媪)
 photo
photo
Kaiyu Yang est chercheur postdoctoral au Département des sciences informatiques et mathématiques (CMS) de Caltech, encadré par Anima Anandkumar.
Il a obtenu son doctorat à l'Université de Princeton, où son superviseur était Jia Deng, et il a également travaillé avec Olga Russakovsky et Chen Danqi.
Ses recherches portent sur l'intelligence artificielle neurosymbolique, qui vise à permettre à l'apprentissage automatique d'effectuer un raisonnement symbolique, en espérant y parvenir à travers deux directions :
(1) Appliquer l'apprentissage automatique à des tâches de raisonnement symbolique, telles que la logique formelle Ou un raisonnement mathématique et une démonstration de théorèmes en langage naturel ;
(2) Introduire des composants symboliques dans les modèles d'apprentissage automatique pour les rendre plus interprétables, vérifiables et efficaces en matière de données.
Actuellement, il travaille sur l'intelligence artificielle capable de comprendre et de raisonner sur les mathématiques. Le raisonnement mathématique constitue une étape importante dans l’intelligence humaine et a le potentiel de transformer de nombreux problèmes importants en science et en ingénierie, tels que la résolution d’équations aux dérivées partielles et la vérification de formules.
Anima Anandkumar
Anima Anandkumar est maintenant professeur de sciences informatiques et mathématiques à Caltech.
 Pictures
Pictures
Ses intérêts de recherche se concentrent principalement sur les domaines de l'apprentissage automatique à grande échelle, de l'optimisation non convexe et des statistiques de grande dimension.
En particulier, elle a dirigé le développement et l'analyse d'algorithmes tensoriels pour l'apprentissage automatique.
La méthode de décomposition tensorielle a un parallélisme et une évolutivité extrêmement élevés et peut être appliquée à des données massives. Il peut garantir la convergence vers la solution optimale et produire des résultats d’estimation cohérents pour de nombreux modèles probabilistes (tels que les modèles de Markov).
Plus largement, le professeur Anandkumar a recherché des techniques efficaces pour accélérer l'optimisation non convexe.
Références :
https://www.php.cn/link/1dd5a4016c624ef51f0542d4ae60e281
https://www.php.cn/link/ed798eec758 07d f6e79b0be391f720e4
https https://www.php.cn/link/a652e914c736dfaf8a6667ae6936f0d6
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

