Le repérage des nuages ​​de points est incontournable pour la vision 3D ! Comprendre toutes les solutions et défis courants dans un seul article

Le nuage de points en tant qu'ensemble de points devrait entraîner un changement dans l'obtention et la génération d'informations de surface tridimensionnelles (3D) d'objets grâce à la reconstruction 3D, à l'inspection industrielle et au fonctionnement de robots. Le processus le plus difficile mais essentiel est l'enregistrement des nuages ​​de points, c'est-à-dire l'obtention d'une transformation spatiale qui aligne et fait correspondre deux nuages ​​de points obtenus dans deux coordonnées différentes. Cette revue présente la vue d'ensemble et les principes de base de l'enregistrement des nuages ​​de points, classe et compare systématiquement diverses méthodes et résout les problèmes techniques existant dans l'enregistrement des nuages ​​de points, en essayant de fournir aux chercheurs universitaires en dehors du domaine et aux ingénieurs des conseils et faciliter les discussions sur une vision unifiée. pour l'enregistrement des nuages ​​de points.

La méthode générale d'acquisition de nuages ​​de points

est divisée en méthodes actives et passives. Le nuage de points activement acquis par le capteur est la méthode active, et la méthode par reconstruction à un stade ultérieur est la méthode passive.

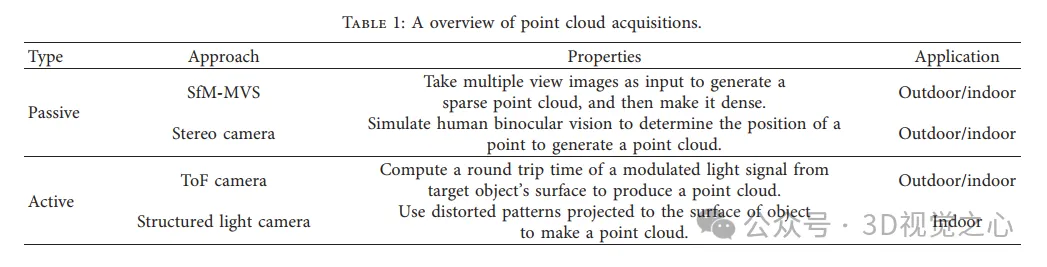
Reconstruction dense de SFM à MVS. (a) GFD. (b) Exemple de nuage de points généré par SfM. (c) Organigramme de l'algorithme PMVS, un algorithme stéréo multi-vues basé sur des correctifs. (d) Exemple de nuage de points dense généré par PMVS.

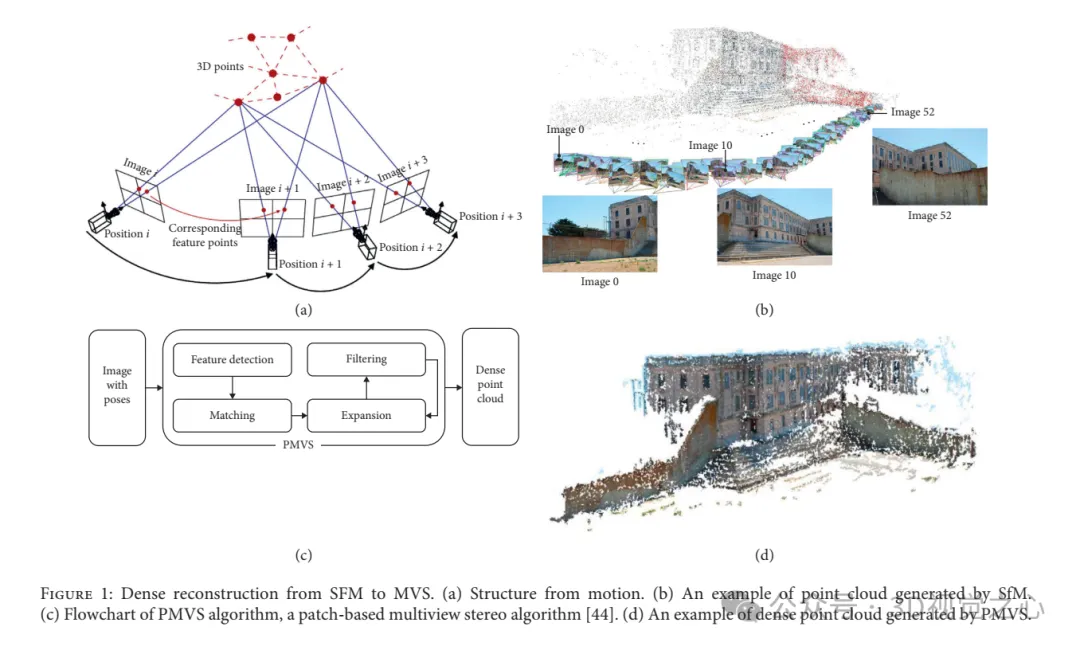
Méthodes de reconstruction de lumière structurée :

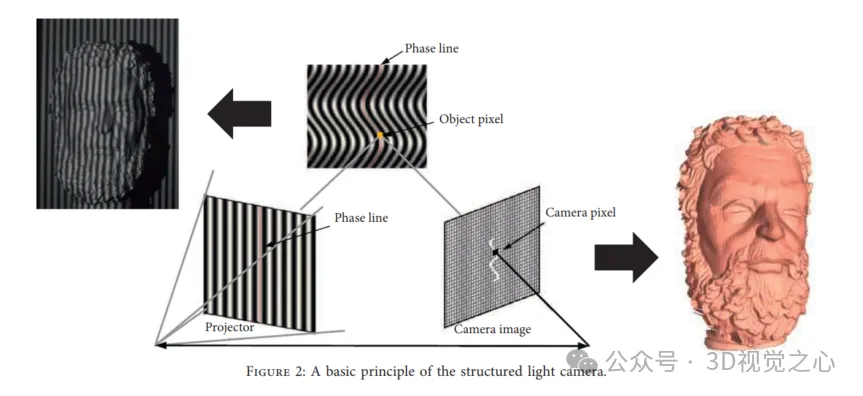
inscription rigide et inscription non rigide

Dans un environnement, la transformation peut être décomposée en rotation et translation Après une transformation rigide appropriée, un nuage de points est mappé sur. un autre nuage de points tout en conservant la même forme et la même taille.

En recalage non rigide, une transformation non rigide est établie pour envelopper les données numérisées dans le nuage de points cible. Les transformations non rigides incluent les réflexions, les rotations, la mise à l'échelle et les traductions, par opposition aux seules traductions et rotations dans le repérage rigide. L'enregistrement non rigide est utilisé pour deux raisons principales : (1) les non-linéarités et les erreurs d'étalonnage dans l'acquisition des données peuvent provoquer une distorsion basse fréquence des numérisations d'objets rigides ; (2) l'enregistrement est effectué sur des scènes ou des objets qui changent de forme et se déplacent au fil du temps ; .

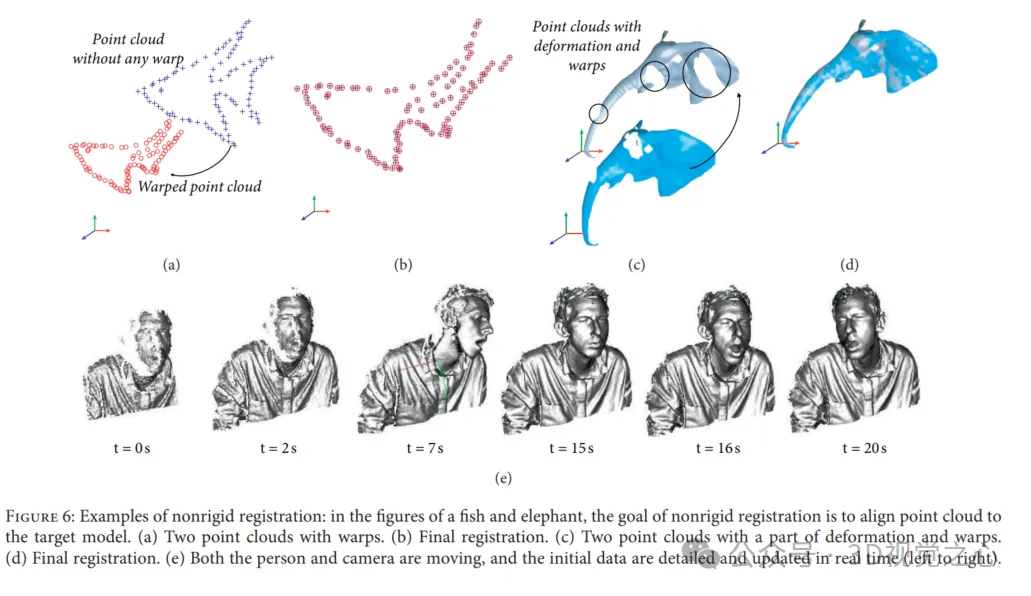
Exemples de recalage rigide : (a) deux nuages ​​de points : nuage de points de lecture (vert) et nuage de points de référence (rouge) ; sans (b) et avec (c) cas d'algorithme de recalage rigide, les nuages ​​de points sont fusionnés ; dans un système de coordonnées commun.

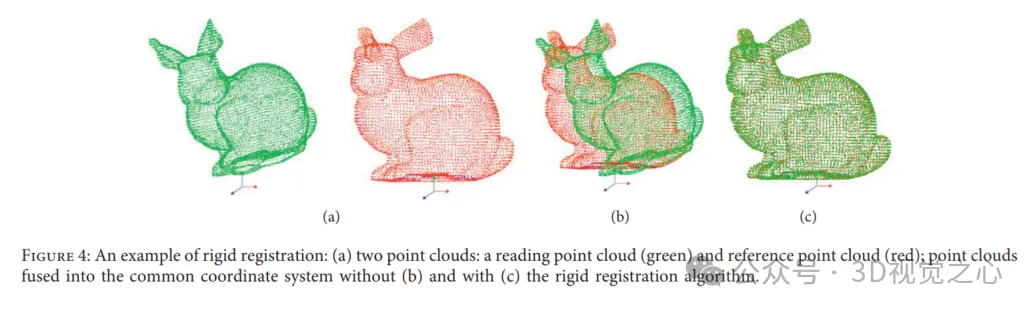
Cependant, les performances de l'enregistrement des nuages ​​de points sont limitées par le chevauchement des variantes, le bruit et les valeurs aberrantes, le coût de calcul élevé et divers indicateurs de réussite de l'enregistrement.

Quelles sont les modalités d'inscription ?

Au cours des dernières décennies, de plus en plus de méthodes d'enregistrement de nuages ​​de points ont été proposées, depuis les algorithmes ICP classiques jusqu'aux solutions combinées à la technologie de deep learning.

1) Schéma ICP

L'algorithme ICP est un algorithme itératif qui peut garantir la précision, la vitesse de convergence et la stabilité de l'enregistrement dans des conditions idéales. Dans un sens, ICP peut être considéré comme un problème de maximisation des attentes (EM), il calcule et met donc à jour de nouvelles transformations basées sur des correspondances, qui sont ensuite appliquées aux données lues jusqu'à ce que la métrique d'erreur converge. Cependant, cela ne garantit pas que l'ICP atteigne l'optimum global. L'algorithme ICP peut être grossièrement divisé en quatre étapes : sélection des points, correspondance des points, rejet des points et minimisation des métriques d'erreur, comme le montre la figure ci-dessous.

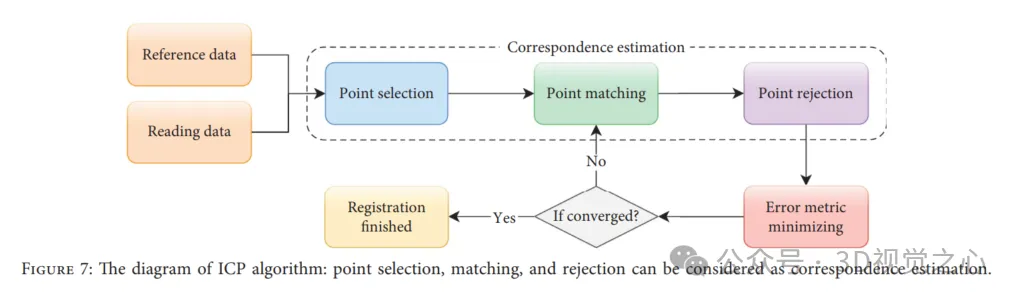
2) Méthodes basées sur les fonctionnalités

Comme nous l'avons vu dans les algorithmes basés sur ICP, il est crucial d'établir une correspondance avant l'estimation de la transformation. Le résultat final est garanti si l'on obtient une correspondance appropriée décrivant la relation correcte entre les deux nuages ​​de points. Par conséquent, nous pouvons coller des points de repère sur la cible numérisée, ou sélectionner manuellement des paires de points équivalentes en post-traitement pour calculer la transformation des points d'intérêt (points sélectionnés), qui peut finalement être appliquée pour lire le nuage de points. Comme le montre la figure 12(c), les nuages ​​​​de points sont chargés dans le même système de coordonnées et dessinés dans des couleurs différentes. Les figures 12(a) et 12(b) montrent deux nuages ​​de points capturés à différents points de vue, avec des paires de points sélectionnées respectivement à partir des données de référence et des données lues, et les résultats d'enregistrement sont présentés sur la figure 12(d). Cependant, ces méthodes ne sont ni adaptées aux objets de mesure auxquels aucun repère n’est attaché, ni applicables aux applications nécessitant un enregistrement automatique. Dans le même temps, afin de minimiser l'espace de recherche des correspondances et d'éviter de supposer des transformations initiales dans les algorithmes basés sur l'ICP, un enregistrement basé sur les caractéristiques est introduit, dans lequel les points clés conçus par les chercheurs sont extraits. Habituellement, la détection des points clés et l’établissement de la correspondance sont les principales étapes de cette méthode.

Les méthodes courantes d'extraction de points clés incluent PFH, SHOT, etc. Il est également important de concevoir un algorithme pour supprimer les valeurs aberrantes et estimer efficacement la transformation basée sur les valeurs internes.

3) Approches basées sur l'apprentissage

Dans les applications qui utilisent des nuages ​​de points comme entrée, les stratégies traditionnelles d'estimation des descripteurs de caractéristiques s'appuient fortement sur les propriétés géométriques uniques des objets dans le nuage de points. Cependant, les données du monde réel sont souvent spécifiques à une cible et peuvent contenir des avions, des valeurs aberrantes et du bruit. De plus, les disparités supprimées contiennent souvent des informations utiles qui peuvent être utilisées pour l’apprentissage. Les techniques basées sur l'apprentissage peuvent être adaptées pour coder des informations sémantiques et peuvent être généralisées à des tâches spécifiques. La plupart des stratégies d'enregistrement intégrées aux techniques d'apprentissage automatique sont plus rapides et plus robustes que les méthodes classiques, et s'étendent de manière flexible à d'autres tâches telles que l'estimation de la pose d'objets et la classification d'objets. De même, un défi clé dans l’enregistrement des nuages ​​de points basé sur l’apprentissage est de savoir comment extraire des caractéristiques invariantes par rapport à la variation spatiale du nuage de points et plus robustes au bruit et aux valeurs aberrantes.

Les représentants des méthodes basées sur l'apprentissage sont : PointNet, PointNet++, PCRNet, Deep Global Registration, Deep Closest Point, Partial Registration Network, Robust Point Matching, PointNetLK, 3DRegNet.

4) Méthode avec fonction de densité de probabilité

L'enregistrement des nuages ​​de points basé sur la fonction de densité de probabilité (PDF) fait de l'enregistrement à l'aide de modèles statistiques un problème bien étudié. L'idée clé de cette méthode est d'utiliser des fonctions de densité de probabilité spécifiques. représentent les données, telles que le modèle de mélange gaussien (GMM) et la distribution normale (ND). La tâche d'enregistrement est reformulée comme un problème d'alignement de deux distributions correspondantes, suivi d'une fonction objectif qui mesure et minimise la différence statistique entre elles. Dans le même temps, grâce à la représentation du PDF, le nuage de points peut être considéré comme une distribution plutôt que comme plusieurs points individuels, il évite donc l'estimation de la correspondance et a de bonnes performances anti-bruit, mais est généralement plus lent que celui basé sur ICP. méthodes.

5) Autres méthodes

Inscription globale rapide. Fast Global Registration (FGR) fournit une stratégie rapide pour l’enregistrement des nuages ​​de points qui ne nécessite aucune initialisation. Plus précisément, FGR opère sur les correspondances candidates de la surface couverte et n'effectue pas de mises à jour de correspondance ni de requêtes de points les plus proches. La particularité de cette approche est qu'elle peut être produite directement par une seule optimisation d'un objectif robuste densément défini sur la surface. inscription. Cependant, les méthodes existantes pour résoudre l'enregistrement des nuages ​​de points génèrent généralement des correspondances candidates ou multiples entre deux nuages ​​de points, puis calculent et mettent à jour les résultats globaux. De plus, dans le recalage global rapide, la correspondance est établie immédiatement lors de l'optimisation et n'est pas réestimée dans les étapes suivantes. Par conséquent, les recherches coûteuses du voisin le plus proche sont évitées afin de maintenir les coûts de calcul à un faible niveau. En conséquence, un traitement linéaire pour chaque correspondance en étapes itératives et un système linéaire d’estimation de pose sont efficaces. FGR est évalué sur plusieurs ensembles de données, tels que le benchmark UWA et Stanford Bunny, par rapport à l'ICP point à point et point-top, ainsi qu'aux variantes d'ICP telles que Go ICP. Les expériences montrent que FGR fonctionne bien en présence de bruit !

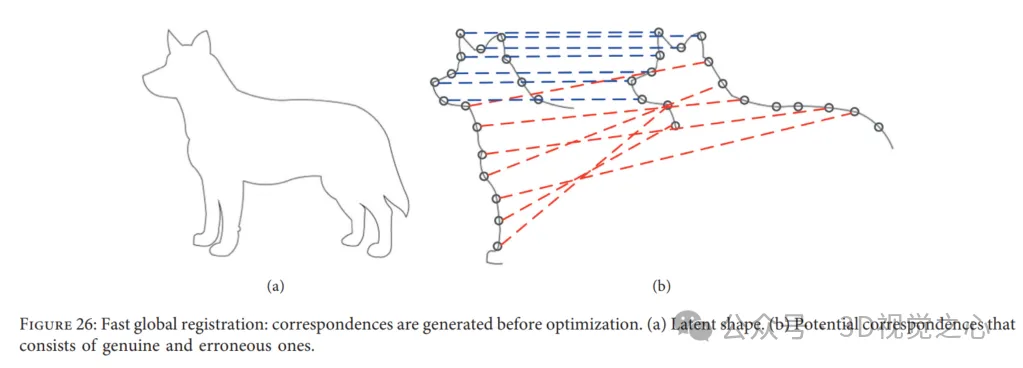
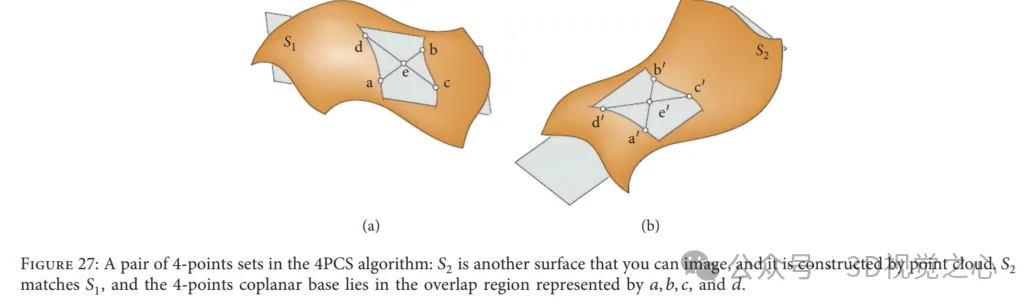
Algorithme d'ensemble congruent à quatre points : un ensemble congruent à 4 points (4PCS) fournit une transformation initiale pour la lecture des données sans hypothèses de position de départ. Généralement, une transformation d'alignement rigide entre deux nuages ​​de points peut être définie de manière unique par une paire de triplets, l'un à partir des données de référence et l'autre à partir des données lues. Cependant, dans cette méthode, il recherche des bases spéciales à 4 points, c'est-à-dire 4 points congrus coplanaires dans chaque nuage de points, en recherchant dans un petit ensemble de potentiels, comme le montre la figure 27. Résoudre la transformation rigide optimale dans le problème du plus grand ensemble de points communs (LCP). Cet algorithme atteint des performances proches lorsque le chevauchement des nuages ​​de points appariés est faible et que des valeurs aberrantes sont présentes. Afin de s’adapter aux différentes applications, de nombreux chercheurs ont introduit des travaux plus importants liés à la solution classique 4PCS.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!