Maison >Périphériques technologiques >IA >Surmonté les trois problèmes majeurs du « modèle basé sur des graphiques » pour la première fois ! HKU open source OpenGraph : l'apprentissage sans échantillon s'adapte à une variété de tâches en aval
Surmonté les trois problèmes majeurs du « modèle basé sur des graphiques » pour la première fois ! HKU open source OpenGraph : l'apprentissage sans échantillon s'adapte à une variété de tâches en aval
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2024-03-15 14:04:16845parcourir
La technologie d'apprentissage graphique a été largement utilisée dans divers domaines, notamment les systèmes de recommandation, l'analyse des réseaux sociaux, les réseaux de citations et les réseaux de transport. Cette technologie peut extraire et apprendre efficacement des données relationnelles complexes, fournissant ainsi un outil puissant aux scientifiques et ingénieurs des données. Grâce aux algorithmes d’apprentissage des graphes, nous pouvons mieux comprendre les associations et les connexions entre les données, nous aidant ainsi à découvrir les lois et les modèles cachés derrière les données. Dans des applications pratiques, la technologie d'apprentissage des graphes peut nous aider à créer des réseaux de neurones graphiques (GNN) plus précis et plus précis en utilisant des mécanismes itératifs de transmission de messages pour capturer des relations complexes d'ordre élevé dans des données structurées en graphiques, dans diverses réalisations remarquables. applications d'apprentissage de graphiques.
Habituellement, ce type de réseau neuronal graphique de bout en bout nécessite une grande quantité de données annotées de haute qualité pour obtenir de meilleurs résultats d'entraînement.
Ces dernières années, certains travaux ont proposé le mode de pré-entraînement et de réglage fin (Pré-entraînement et Réglage fin) des modèles de graphiques, en utilisant diverses tâches d'apprentissage auto-supervisées pour d'abord pré-entraîner sur des données graphiques non étiquetées. , puis effectuez une formation sur une petite quantité de données. Un réglage fin est effectué sur les données étiquetées pour lutter contre le problème des signaux de supervision insuffisants. Les tâches d'apprentissage auto-supervisées incluent ici des méthodes telles que l'apprentissage contrastif, la reconstruction de masques et la maximisation des informations mutuelles locales et globales.
Bien que de telles méthodes de pré-formation réussissent dans une certaine mesure, elles présentent certaines limites en termes de capacités de généralisation, en particulier lorsque des changements de répartition se produisent entre la pré-formation et les tâches en aval.
Dans les systèmes de recommandation, les modèles pré-entraînés sont formés sur la base des premières données, mais les préférences des utilisateurs et la popularité des produits changent souvent, ce qui nécessite que le modèle soit constamment mis à jour pour s'adapter aux nouvelles informations.
Pour relever ce défi, des recherches récentes ont proposé des méthodes de réglage fin des indices pour les modèles graphiques, afin que les modèles pré-entraînés puissent s'adapter plus efficacement aux différentes tâches et données en aval.
Bien que les recherches ci-dessus aient favorisé les performances de généralisation des modèles de réseaux neuronaux graphiques, ces modèles sont basés sur une hypothèse : les données d'entraînement et les données de test ont le même ensemble de nœuds et le même espace de fonctionnalités.
Cela limite considérablement le champ d'application des modèles graphiques pré-entraînés. Par conséquent, cet article explore des méthodes permettant d’améliorer davantage la capacité de généralisation des modèles graphiques.
Nous espérons qu'OpenGraph capturera des modèles structurels topologiques courants et réalisera des prédictions sans tir sur les données de test. Cela signifie que grâce au processus de propagation vers l'avant, les caractéristiques peuvent être extraites efficacement et les données des graphiques de test prédites avec précision.
Le processus de formation du modèle est effectué sur des données graphiques complètement différentes, et aucun élément du graphique de test, y compris les nœuds, les arêtes et les vecteurs de caractéristiques, n'est touché pendant la phase de formation.
Afin d'atteindre cet objectif, cet article doit résoudre les trois défis suivants : 
C1. Modifications des ensembles de jetons dans les ensembles de données
Une difficulté importante dans la prédiction du graphique à échantillon nul. La tâche est que différentes données graphiques ont généralement des ensembles de jetons graphiques complètement différents. Plus précisément, les ensembles de nœuds de différents graphiques ne se chevauchent souvent pas, et différents ensembles de données graphiques utilisent souvent des fonctionnalités de nœuds complètement différentes. Cela empêche le modèle d'effectuer des tâches de prédiction entre ensembles de données en apprenant des paramètres liés aux jetons graphiques d'un ensemble de données spécifique.
C2. Modélisation efficace des relations entre les nœuds
Dans le domaine de l'apprentissage des graphes, il existe souvent des dépendances complexes entre les nœuds et le modèle doit prendre en compte de manière globale les relations de voisinage locales et globales des nœuds. Lors de la création d'un modèle graphique général, une tâche importante consiste à être capable de modéliser efficacement les relations entre les nœuds, ce qui peut améliorer l'effet et l'évolutivité du modèle lors du traitement de grandes quantités de données graphiques.
C3. Rareté des données de formation
En raison de la protection de la vie privée, des coûts de collecte de données et d'autres raisons, les problèmes de rareté des données sont répandus dans de nombreux domaines en aval de l'apprentissage des graphes, ce qui rend la formation de modèles de graphes généraux sujette à un manque. de prise en charge de certains résultats de formation sous-optimaux en raison d'un manque de compréhension des domaines en aval.
Pour relever les défis ci-dessus, des chercheurs de l'Université de Hong Kong ont proposé OpenGraph, un modèle performant en matière d'apprentissage sans tir et capable d'identifier des modèles structurels topologiques transférables entre différents domaines en aval.

Lien papier : https://arxiv.org/pdf/2403.01121.pdf
Lien du code source : https://github.com/HKUDS/OpenGraph
En créant une topologie projection Le tokenizer graphique proposé résout le défi C1, générant ainsi des jetons graphiques unifiés.
Pour relever le défi C2, un transformateur graphique évolutif est conçu, équipé d'un mécanisme d'auto-attention efficace basé sur l'échantillonnage d'ancres et comprend un échantillonnage de séquences de jetons pour obtenir une formation plus efficace.
Pour relever le défi C3, nous exploitons de grands modèles de langage pour l'augmentation des données afin d'enrichir notre pré-formation, en utilisant des algorithmes d'arbres d'indices et l'échantillonnage de Gibbs pour simuler des données relationnelles structurées sous forme de graphiques du monde réel. Nos tests approfondis sur plusieurs ensembles de données graphiques montrent les capacités de généralisation supérieures d'OpenGraph dans une variété de paramètres.
Introduction au modèle
L'architecture globale du modèle est présentée dans la figure ci-dessous, qui peut être divisée en trois parties, à savoir 1) Tokenizer de graphe unifié, 2) Transformateur de graphe évolutif, 3) distillation des connaissances d'un grand modèle de langage .

Tokenizer de graphique unifié
Afin de faire face aux énormes différences de nœuds, d'arêtes et de caractéristiques des différents ensembles de données, notre première tâche est de construire un graphe unifié. tokenizer , qui peut mapper efficacement différentes données graphiques dans une séquence de jetons unifiée. Dans notre tokenizer, chaque jeton possède un vecteur sémantique qui décrit les informations du nœud correspondant.
En adoptant un espace de représentation de nœuds unifié et une structure de données de séquence flexible, nous espérons effectuer une tokenisation standardisée et efficace pour différentes données graphiques.
Pour atteindre cet objectif, notre tokenizer utilise des informations topologiques lissées et une fonction de mappage de l'espace des nœuds à l'espace de représentation latente.
Matrice de contiguïté lisse d'ordre élevé
Dans le processus de tokenisation du graphique, la puissance d'ordre élevé de la matrice de contiguïté est utilisée comme l'une des entrées. Cette méthode peut non seulement obtenir le haut-. relation de connexion d'ordre de la structure du graphe, mais résout également le problème de la rareté des connexions dans les matrices de contiguïté originales.
La normalisation laplacienne est effectuée pendant le processus de calcul, et toutes les puissances matricielles de contiguïté d'ordres différents sont prises en compte. La méthode de calcul spécifique est la suivante.
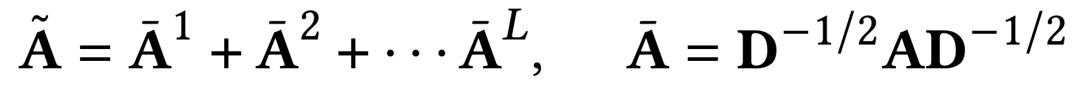
Cartographie de graphiques arbitraires tenant compte de la topologie
Les matrices de contiguïté de différents ensembles de données présentent d'énormes différences de dimensions, ce qui nous empêche de prendre directement la matrice de contiguïté en entrée, puis d'utiliser une entrée fixe Traitement du réseau neuronal dimensionnel.
Notre solution consiste d'abord à projeter la matrice d'adjacence sous la forme d'une séquence de représentation de nœuds, puis à utiliser un modèle de séquence de longueur variable pour le traitement. Afin de réduire la perte d'informations dans le processus de mappage, nous proposons une méthode de mappage prenant en compte la topologie.
Tout d'abord, la plage de valeurs de notre mappage sensible à la topologie est un espace de représentation latent de dimension supérieure. Certains travaux antérieurs ont souligné que même des mappages aléatoires peuvent souvent produire des représentations satisfaisantes en adoptant des dimensions d’espace latent plus grandes.
Afin de préserver davantage les informations sur la structure du graphe et de réduire l'impact du caractère aléatoire, nous utilisons la décomposition rapide des valeurs propres (SVD) pour construire notre fonction de cartographie. Dans les expériences réelles, deux cycles de décomposition rapide des valeurs propres peuvent conserver efficacement les informations topologiques, et la surcharge de calcul qui en résulte est négligeable par rapport aux autres modules.
Scalable Graph Transformer
Après un processus de tokenisation de graphe sans paramètre, OpenGraph attribue une représentation unifiée de jeton de graphe prenant en compte la topologie pour représenter graphiquement des données avec différentes caractéristiques. La tâche suivante consiste à modéliser les dépendances complexes entre les nœuds à l'aide de réseaux neuronaux entraînables.
OpenGraph adopte l'architecture du transformateur pour profiter de ses puissantes capacités de modélisation de relations complexes. Afin de garantir l'efficacité et les performances du modèle, nous introduisons les deux techniques d'échantillonnage suivantes.
Échantillonnage de séquence de jetons
Étant donné que nos données de séquence de jetons graphiques comportent généralement un grand nombre de jetons et de dimensions de représentation cachées, le transformateur graphique utilisé par OpenGraph échantillonne la séquence de jetons d'entrée et n'apprend que le lot d'entraînement actuel. les relations par paires entre les jetons au cours d'une période donnée réduisent le nombre de paires de relations qui doivent être modélisées du carré du nombre de nœuds au carré de la taille du lot de formation, réduisant ainsi considérablement la surcharge de temps et d'espace du transformateur graphique dans la formation phase. De plus, cette méthode d'échantillonnage permet au modèle d'accorder plus d'attention au lot d'entraînement en cours lors de l'entraînement.
Bien que les données d'entrée soient échantillonnées, puisque notre représentation initiale du jeton graphique contient la relation topologique entre les nœuds, la séquence de jetons échantillonnée peut toujours refléter les informations de tous les nœuds du graphique entier dans une certaine mesure.
Méthode d'échantillonnage d'ancrage dans l'auto-attention
Bien que l'échantillonnage de séquence de jetons réduise la complexité du carré du nombre de nœuds au carré de la taille du lot, la complexité au niveau du carré a un plus grand impact sur la taille du lot La limitation rend impossible l'utilisation de lots plus grands pour la formation du modèle, affectant ainsi le temps de formation global et la stabilité de la formation.
Afin d'atténuer ce problème, la partie transformateur d'OpenGraph abandonne la modélisation de la relation par paire entre tous les jetons. Au lieu de cela, elle échantillonne certains points d'ancrage et divise l'apprentissage des relations entre tous les nœuds en deux fois.
Distillation des connaissances sur un grand modèle de langage
En raison de la confidentialité des données et d'autres raisons, il est très difficile d'obtenir des données de divers domaines pour former un modèle de graphique général. Ressentant les étonnantes capacités de connaissance et de compréhension démontrées par les grands modèles de langage (LLM), nous exploitons sa puissance pour générer diverses données structurées en graphes pour la formation de modèles de graphes généraux.
Le mécanisme d'augmentation des données que nous avons conçu permet aux données graphiques améliorées par LLM de mieux se rapprocher des caractéristiques des graphiques du monde réel, améliorant ainsi la pertinence et l'utilité des données augmentées.
Génération de nœuds basée sur LLM
Lors de la génération d'un graphique, notre première étape consiste à créer un ensemble de nœuds adapté à un scénario d'application spécifique. Chaque nœud possède une description textuelle des fonctionnalités qui facilite le processus de génération de contours ultérieur.
Cependant, lorsqu'il s'agit de scénarios du monde réel, cette tâche peut être particulièrement difficile en raison de la grande taille de l'ensemble de nœuds. Par exemple, sur une plateforme de commerce électronique, les données graphiques peuvent contenir des milliards de produits. Par conséquent, permettre efficacement à LLM de générer un grand nombre de nœuds devient un défi important.
Pour relever les défis ci-dessus, nous adoptons une stratégie consistant à diviser continuellement les nœuds généraux en sous-catégories plus fines.
Par exemple, lors de la génération de nœuds de produits dans un scénario de commerce électronique, utilisez d'abord une invite de requête LLM similaire à « Répertorier les sous-catégories de tous les produits sur les plateformes de commerce électronique telles que Taobao ». LLM a répondu avec une liste de sous-catégories telles que « Vêtements », « Ustensiles de cuisine pour la maison » et « Électronique ».
Ensuite, nous demandons à LLM d'affiner davantage chaque sous-catégorie pour poursuivre ce processus de division itératif. Ce processus est répété jusqu'à ce que nous obtenions des nœuds qui ressemblent à des instances du monde réel, comme un nœud avec les étiquettes « vêtements », « vêtements pour femmes », « pull », « pull à poches » et « pull à poches blanc » Le produit.
Algorithme d'arbre d'invite
Le processus de division des nœuds en sous-catégories et de génération d'entités à granularité fine suit une structure arborescente. Les nœuds généraux initiaux (par exemple « produit », « document d'apprentissage en profondeur ») servent de racines et les entités à granularité fine servent de nœuds feuilles. Nous adoptons une stratégie d'indication d'arbre pour parcourir et générer ces nœuds.

Génération d'arêtes basée sur l'échantillonnage LLM et Gibbs
Pour générer des arêtes, nous utilisons l'algorithme d'échantillonnage de Gibbs avec l'ensemble de nœuds généré ci-dessus. L'algorithme part d'un échantillon aléatoire et itère à chaque fois, sur la base de l'échantillon actuel, un échantillon obtenu en modifiant l'une des dimensions des données est échantillonné.
La clé de cet algorithme est d'estimer la probabilité conditionnelle qu'une certaine dimension de données change dans les conditions de l'échantillon actuel. Nous proposons d'effectuer une estimation de probabilité par LLM sur la base des caractéristiques du texte obtenues lors de la génération des nœuds.
Étant donné que l'espace défini des arêtes est grand, afin d'éviter l'énorme surcharge causée par le fait de laisser LLM l'explorer, nous utilisons d'abord LLM pour caractériser l'ensemble de nœuds, puis utilisons un simple opérateur de similarité pour caractériser les nœuds en fonction de le vecteur de représentation. Calculez la relation entre eux. Dans le cadre de génération de bords ci-dessus, nous adoptons également les trois techniques importantes d'ajustement suivantes.
Normalisation de probabilité dynamique
Étant donné que la similarité de la représentation LLM peut être significativement différente de la plage [0, 1], afin d'obtenir une valeur de probabilité plus adaptée à l'échantillonnage, nous utilisons une normalisation de probabilité dynamique Méthodes.
Cette méthode maintient dynamiquement les valeurs d'estimation de similarité T' les plus récentes pendant le processus d'échantillonnage, calcule leur moyenne et leur écart type, et enfin mappe l'estimation de similarité actuelle à la plage de distribution de deux écarts types au-dessus et en dessous de la moyenne. . Cela donne une estimation de probabilité d'environ [0, 1].
Présentation de la localité des nœuds
La méthode de génération de bords basée sur LLM peut déterminer efficacement leurs relations de connexion potentielles en fonction de la similarité sémantique des nœuds.
Cependant, cela a tendance à créer trop de connexions entre tous les nœuds sémantiquement liés, ignorant le concept important de localité dans les graphiques du monde réel.
Dans le monde réel, les nœuds sont plus susceptibles d'être connectés à un sous-ensemble de nœuds associés car ils n'ont généralement qu'une interaction limitée avec un sous-ensemble de nœuds. Pour modéliser cette propriété importante, une méthode prenant en compte la localité lors de la génération des arêtes est introduite.
Chaque nœud se voit attribuer au hasard un indice de localité. La probabilité d'interaction entre deux nœuds est affectée par l'atténuation de la différence absolue de l'indice de localité. Plus la différence dans l'indice de localité des nœuds est grande, plus l'atténuation est grave. sera.
Injecter un modèle de topologie de graphe
Afin de rendre les données du graphe générées plus cohérentes avec le modèle de structure topologique, nous générons à nouveau des représentations de nœuds modifiées au cours du premier processus de génération de graphe.
Cette représentation de nœud est obtenue sur le graphique généré initialement à l'aide d'un simple réseau de convolution graphique. Elle peut mieux se conformer aux caractéristiques de distribution des données structurées par graphique et éviter les changements de distribution entre le graphique et l'espace texte. Enfin, sur la base de la représentation révisée des nœuds, nous effectuons à nouveau un échantillonnage graphique pour obtenir les données finales de la structure graphique.
Vérification expérimentale
Dans l'expérience, nous avons utilisé uniquement l'ensemble de données généré basé sur LLM pour la formation du modèle OpenGraph, et les ensembles de données de test sont de véritables ensembles de données dans divers scénarios d'application et incluent la classification et la chaîne de nœuds Il existe deux types de tâches de prévision routière. Les paramètres spécifiques de l'expérience sont les suivants :
Réglage 0-shot
Afin de vérifier la capacité de prédiction sans échantillon d'OpenGraph, OpenGraph a été testé sur l'ensemble de données d'entraînement généré, puis utilisé un ensemble de données de test réel complètement différent Effectuer des tests d'effet. Il n'y a pas de chevauchement entre l'ensemble de données d'entraînement et l'ensemble de données de test en termes de nœuds, d'arêtes, de fonctionnalités et d'étiquettes.
Paramètres de quelques tirs
Étant donné que la plupart des méthodes existantes ne peuvent pas effectuer de prédiction efficace de zéro tir, nous utilisons la prédiction de quelques tirs pour les tester. Les méthodes de base peuvent être pré-entraînées sur des données de pré-entraînement, puis entraînées, affinées ou suggérées pour être affinées à l'aide d'échantillons k-shot.
Comparaison de l'effet global
Les résultats des tests sur 2 tâches et un total de 8 ensembles de données de test sont les suivants.
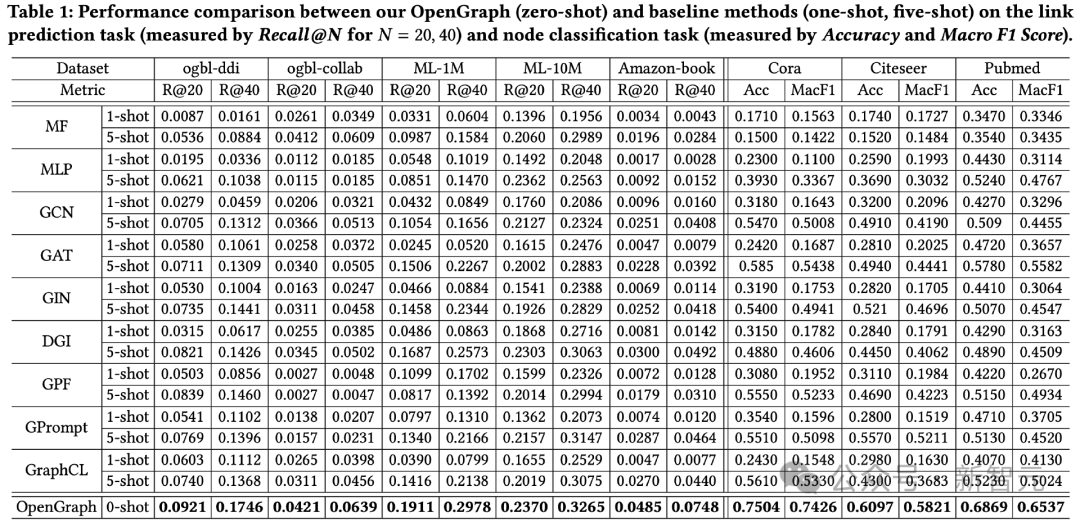
On peut observer :
1) Dans le cas d'ensembles de données croisés, l'effet de prédiction à échantillon nul d'OpenGraph a un plus grand avantage que les méthodes existantes.
2) Dans le cas de migration cross-dataset, les méthodes de pré-entraînement existantes sont parfois encore pires que leurs modèles de base qui ne sont entraînés de zéro que sur quelques échantillons, ce qui reflète la capacité des modèles de graphes à obtenir des cross-datasets. Généralisation des ensembles de données Difficultés.
Graph Tokenizer Research
Ensuite, nous explorons l'impact de la conception du tokenizer d'image sur l'effet. Nous avons d’abord ajusté l’extrémité de lissage de la matrice de contiguïté et testé son impact sur l’effet. L’effet est fortement atténué à l’ordre 0, ce qui indique l’importance d’utiliser un lissage d’ordre supérieur.
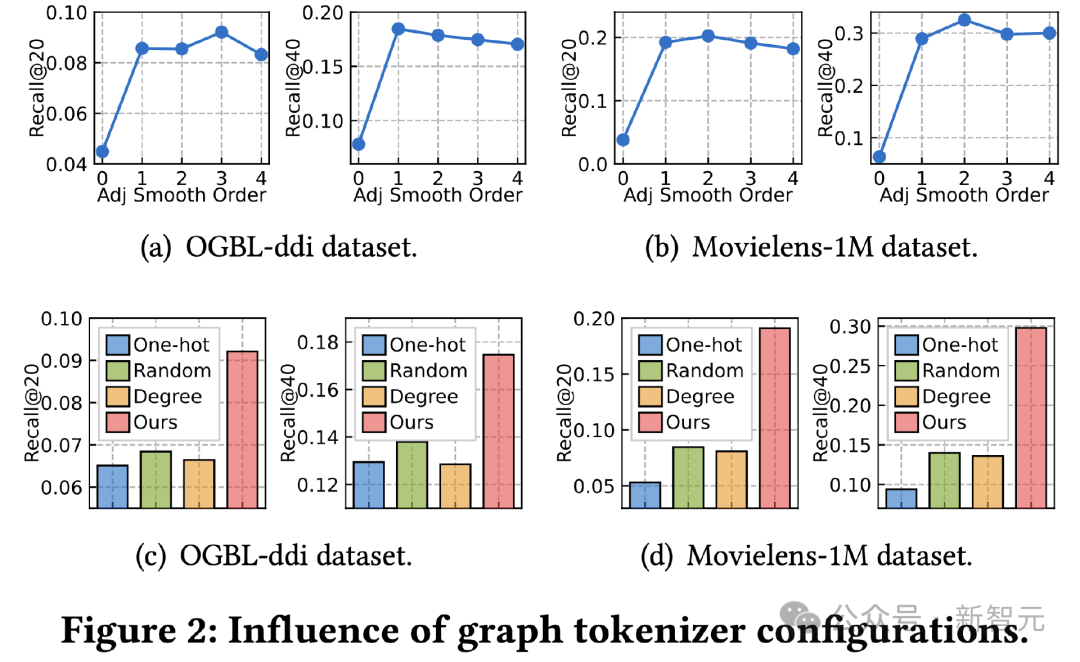
Deuxièmement, nous remplaçons la fonction de mappage prenant en compte la topologie par d'autres méthodes simples, notamment la représentation d'identifiant unique apprenable sur des ensembles de données, le mappage aléatoire et la représentation apprenable basée sur le degré de nœud.
Les résultats montrent que les trois alternatives sont moins efficaces. Parmi elles, l'apprentissage de la représentation des identifiants dans les ensembles de données a le pire effet. L'effet de représentation des diplômes couramment utilisé dans les travaux existants atténue également considérablement l'effet. toutes les méthodes alternatives fonctionnent mieux, mais sont encore loin de notre cartographie tenant compte de la topologie.
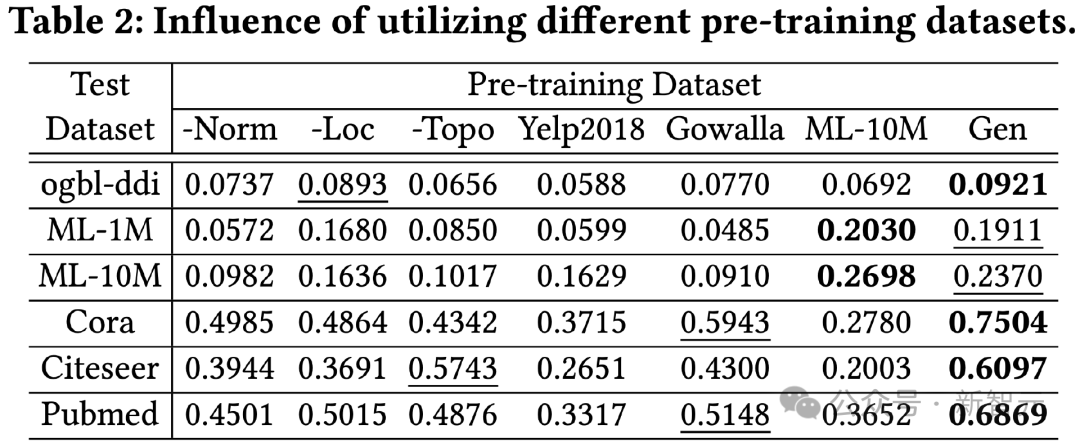
Recherche d'ensembles de données pré-entraînement
Afin de vérifier l'efficacité de la méthode de distillation des connaissances basée sur LLM, nous utilisons différents ensembles de données pré-entraînement pour entraîner OpenGraph et le tester sur différents ensembles de tests sur l'effet.
Les ensembles de données de pré-entraînement comparés dans cette expérience incluent une version qui supprime une certaine astuce dans notre seule méthode de génération, deux ensembles de données réels Yelp2018 et Gowalla qui ne sont pas liés à l'ensemble de données de test, et liés au ML l'ensemble de données de test. 10M d'ensemble de données, cela peut être vu à partir des résultats :
1) Dans l'ensemble, notre ensemble de données généré peut produire de meilleurs résultats sur toutes les données de test.
2) Les techniques de trois générations testées ont toutes un effet d'amélioration significatif.
3) L'utilisation d'ensembles de données réels (Yelp, Gowalla) pour l'entraînement peut avoir des effets négatifs, qui peuvent être dus aux différences de distribution entre les différents ensembles de données réels.
4) ML-10M a obtenu les meilleurs résultats sur ML-1M et ML-10M, ce qui montre que l'utilisation d'ensembles de données d'entraînement similaires peut produire de meilleurs résultats.
Recherche sur les techniques d'échantillonnage dans Transformer
Cette expérience a mené un test d'ablation sur l'échantillonnage de séquences de jetons (Seq) et l'échantillonnage d'ancres (Anc) dans notre module de transformateur graphique.
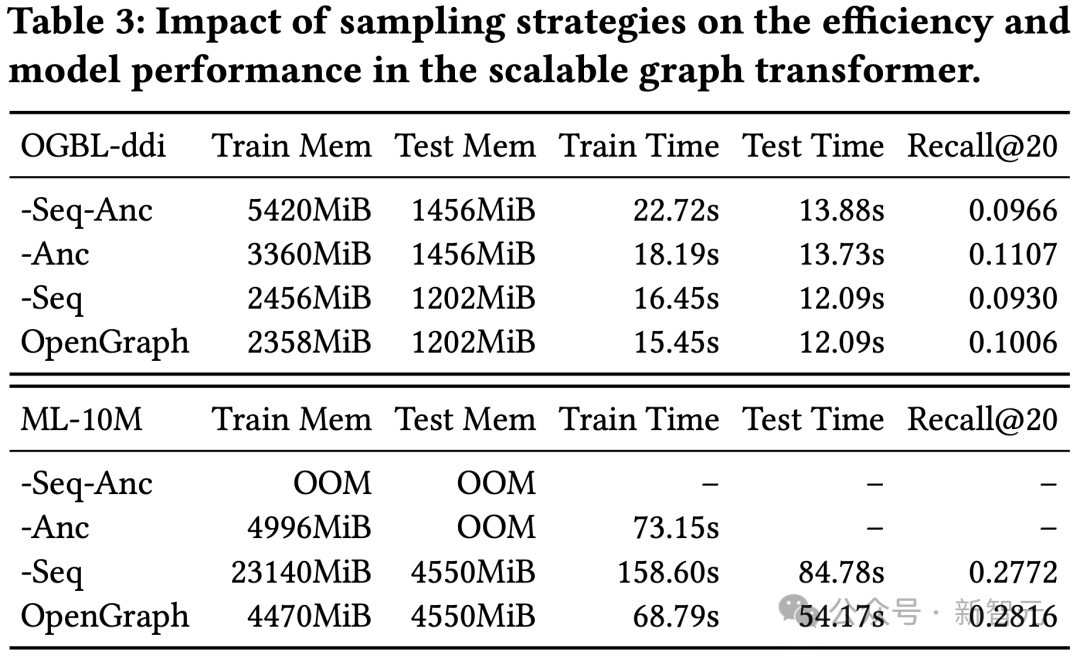
Les résultats montrent que les deux méthodes d'échantillonnage peuvent optimiser la surcharge spatiale et temporelle du modèle pendant le processus de formation et de test. En termes d'effet, l'échantillonnage de séquences de jetons a un effet positif sur l'effet de modèle, tandis que les résultats sur l'ensemble de données ddi montrent que l'échantillonnage par parabole d'ancrage a un effet négatif sur l'effet de modèle.
Conclusion
L'objectif principal de cette recherche est de développer un cadre hautement adaptable capable de capturer et de comprendre avec précision des modèles topologiques complexes dans diverses structures de graphes.
En exploitant le potentiel du modèle proposé, nous visons à améliorer considérablement la capacité de généralisation du modèle pour qu'il fonctionne bien dans les tâches d'apprentissage de graphes zéro-shot, y compris diverses applications en aval.
Pour améliorer encore l'efficacité et la robustesse d'OpenGraph, nous avons construit notre modèle basé sur une architecture de transformateur graphique évolutive et un mécanisme d'augmentation de données basé sur LLM.
Grâce à des expériences approfondies sur plusieurs ensembles de données de référence, nous avons vérifié les capacités de généralisation exceptionnelles du modèle. Cette étude fait une tentative d’exploration préliminaire dans le sens du modèle à base de graphes.
Dans les travaux futurs, nous prévoyons de permettre à notre framework de découvrir automatiquement des connexions et des structures bruyantes avec une influence d'apprentissage contrefactuelle, tout en apprenant des modèles structurels généraux et transférables pour divers graphiques.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- comment créer une base de données SQL
- Quelles sont les couches du modèle de référence TCP/IP ?
- Comment importer des données d'un tableau Excel dans un autre tableau
- PHP implémente des fonctions de réseaux sociaux
- Application intégrée de PHP, Unity3D et Workerman : comment construire un nouveau réseau social

