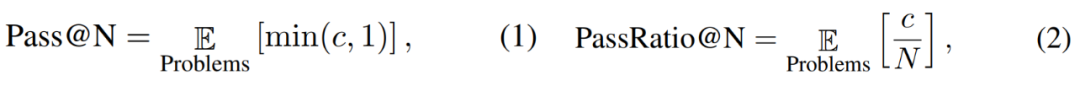Les données synthétiques continuent de libérer le potentiel de raisonnement mathématique des grands modèles !
La capacité à résoudre des problèmes mathématiques a toujours été considérée comme un indicateur important du niveau d'intelligence des modèles de langage. Habituellement, seuls les très grands modèles ou les modèles ayant subi une pré-formation mathématique approfondie ont une chance de bien performer sur des problèmes mathématiques. Récemment, un travail de recherche Xwin créé par l'équipe Swin-Transformer et réalisé conjointement par des chercheurs de l'Université Xi'an Jiaotong, de l'Université des sciences et technologies de Chine, de l'Université Tsinghua et de Microsoft Research Asia a renversé cette perception et révélé le Le modèle de langage à l'échelle 7B (c'est-à-dire 7 milliards de paramètres) (LLaMA-2-7B) sous pré-formation générale a montré un fort potentiel dans la résolution de problèmes mathématiques et peut utiliser des méthodes de réglage fin supervisées basées sur des données synthétiques pour rendre le modèle de plus en plus parfait. Stimulation constante des capacités mathématiques. Cette étude a été publiée sur arXiv, intitulée "Les modèles de langage 7B communs possèdent déjà de fortes capacités mathématiques". 
- Lien papier : https://arxiv.org/pdf/2403.04706.pdf
- Lien code : https://github.com/Xwin-LM/Xwin-LM
L'équipe de recherche a d'abord utilisé seulement 7,5K données pour affiner les instructions du modèle LLaMA-2-7B, puis a évalué les performances du modèle en GSM8K et MATH. Les résultats expérimentaux montrent que lors de la sélection de la meilleure réponse parmi 256 réponses générées pour chaque question de l'ensemble de tests, la précision du test peut atteindre respectivement 97,7 % et 72,0 %. Ce résultat montre que même dans le cadre d'une pré-formation générale, le niveau 7B est atteint. La découverte selon laquelle même les petits modèles ont le potentiel de générer des réponses de haute qualité remet en question l’opinion précédente selon laquelle le potentiel d’un raisonnement mathématique puissant ne se limite pas aux modèles pré-entraînés à grande échelle et liés mathématiquement. 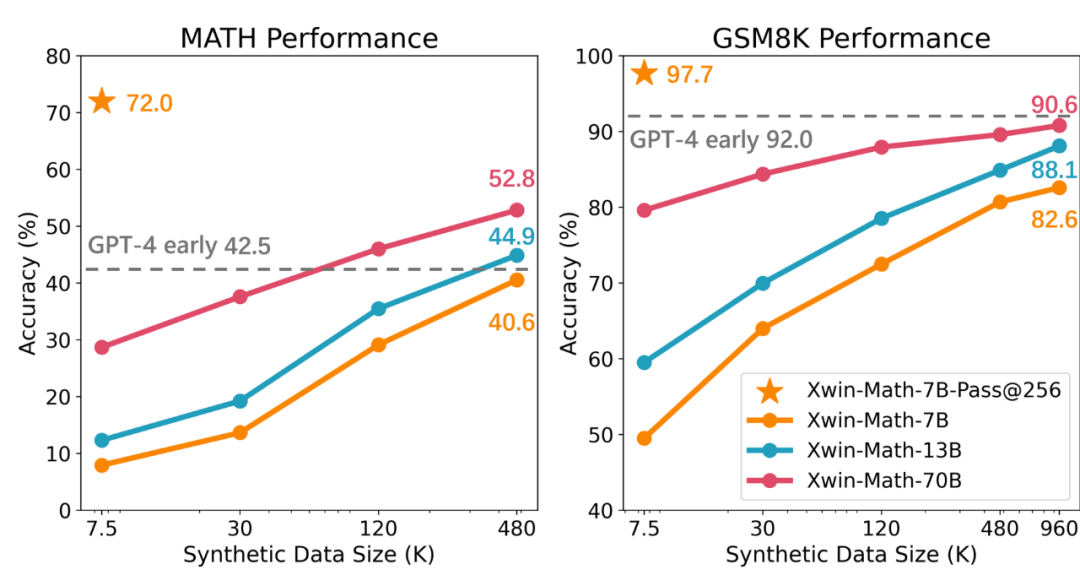
Cependant, les recherches soulignent également que malgré leur fort potentiel de raisonnement mathématique, le principal problème des modèles de langage actuels est qu'il est difficile de stimuler de manière cohérente leurs capacités mathématiques inhérentes. Par exemple, si une seule réponse générée par question était prise en compte dans l'expérience précédente, la précision des tests GSM8K et MATH chuterait à 49,5 % et 7,9 %, respectivement. Cela reflète l'instabilité des capacités mathématiques du modèle. Pour résoudre ce problème, l'équipe de recherche a adopté la méthode d'expansion de l'ensemble de données de réglage fin supervisé (SFT) et a constaté qu'avec l'augmentation des données SFT, la fiabilité du modèle dans la génération de réponses correctes était considérablement améliorée. L'étude a également mentionné qu'en utilisant des données synthétiques, l'ensemble de données SFT peut être efficacement élargi, et cette méthode est presque aussi efficace que les données réelles. L'équipe de recherche a utilisé l'API GPT-4 Turbo pour générer des questions mathématiques synthétiques et des processus de résolution de problèmes, et a assuré la qualité des questions grâce à de simples mots d'invite de vérification. Grâce à cette méthode, l’équipe a réussi à étendre l’ensemble de données SFT de 7,5 000 à environ un million d’échantillons, obtenant ainsi une loi d’échelle presque parfaite. Le modèle Xwin-Math-7B résultant a atteint une précision de 82,6 % et 40,6 % sur GSM8K et MATH respectivement, dépassant considérablement les modèles SOTA précédents et dépassant même certains modèles 70B, réalisant une amélioration révolutionnaire. Le modèle Xwin-Math-70B a obtenu un résultat de 52,8 % sur l'ensemble d'évaluation MATH, dépassant largement la première version de GPT-4. C’est la première fois que la recherche basée sur la série de modèles de base LLaMA dépasse GPT-4 sur MATH. 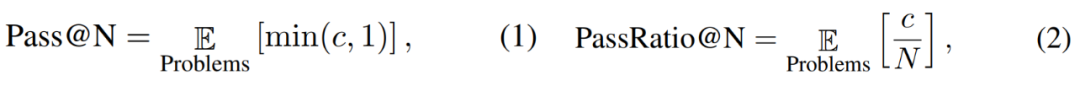
Les chercheurs ont également défini les indicateurs d'évaluation Pass@N et PassRatio@N, dans le but d'évaluer si le modèle peut produire la bonne réponse (indiquant la capacité mathématique potentielle du modèle) et la proportion de réponses correctes parmi les N résultats du modèle. Échelle (indiquant la stabilité des capacités mathématiques du modèle). Lorsque la quantité de données SFT est faible, le Pass@256 du modèle est déjà très élevé. Après avoir encore élargi l'échelle des données SFT, le Pass@256 du modèle augmente très peu, tandis que le PassRatio@256 augmente considérablement. Cela montre que le réglage fin supervisé basé sur des données synthétiques est un moyen efficace d’améliorer la stabilité des capacités mathématiques du modèle. 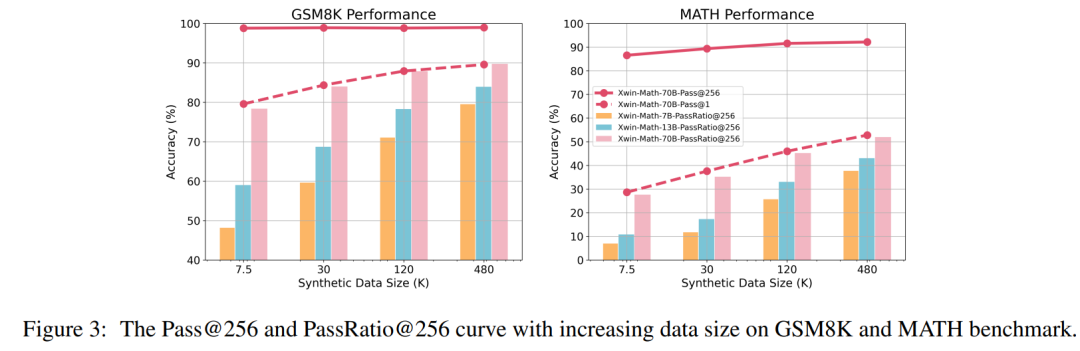
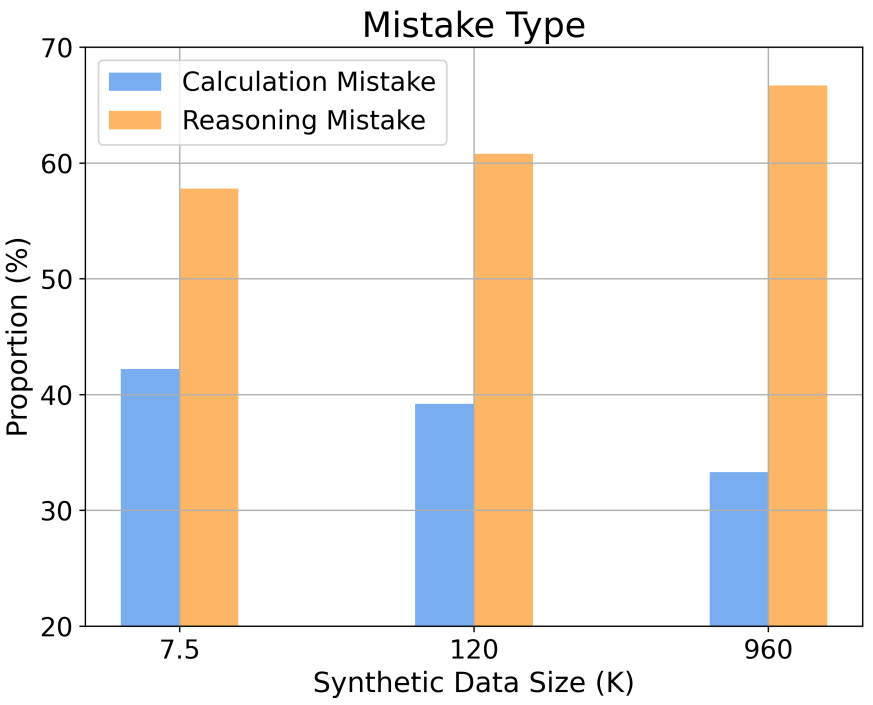
De plus, l'étude fournit des informations sur le comportement de mise à l'échelle selon différentes complexités de raisonnement et types d'erreurs. Par exemple, à mesure que la taille de l'ensemble de données SFT augmente, la précision du modèle dans la résolution de problèmes mathématiques suit une relation de loi de puissance avec le nombre d'étapes d'inférence. En augmentant la proportion de longues étapes d'inférence dans les échantillons d'apprentissage, la précision du modèle dans la résolution de problèmes difficiles peut être considérablement améliorée. Dans le même temps, l’étude a également révélé que les erreurs de calcul sont plus faciles à atténuer que les erreurs de raisonnement. 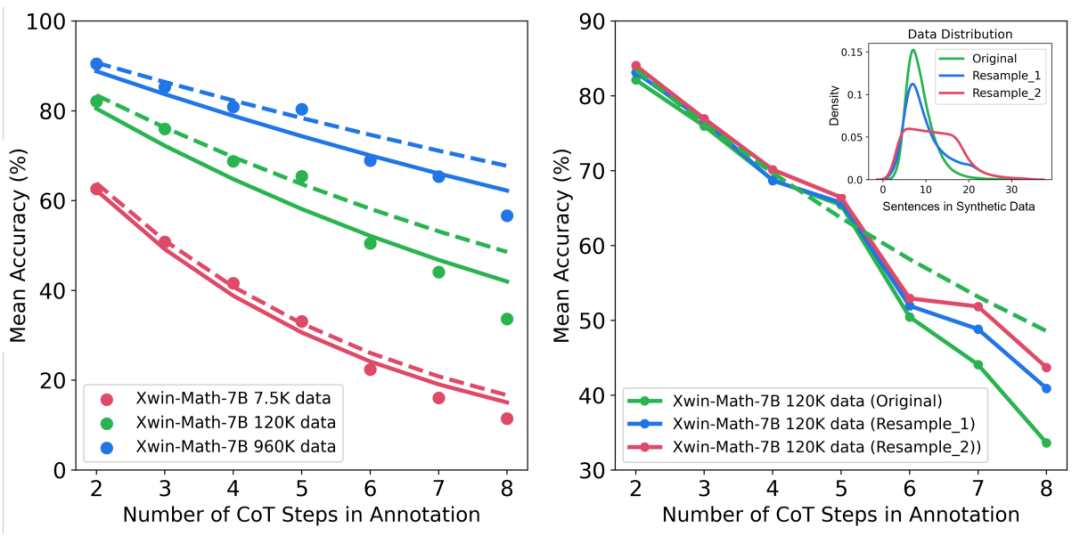
Lors de l'examen de mathématiques du lycée hongrois, qui montre la capacité de généralisation du raisonnement mathématique du modèle, Xwin-Math a également obtenu un score de 65 %, juste derrière GPT-4. Cela montre que la manière dont les données ont été synthétisées dans l’étude ne s’est pas trop adaptée à l’ensemble d’évaluation et a montré une bonne capacité de généralisation. 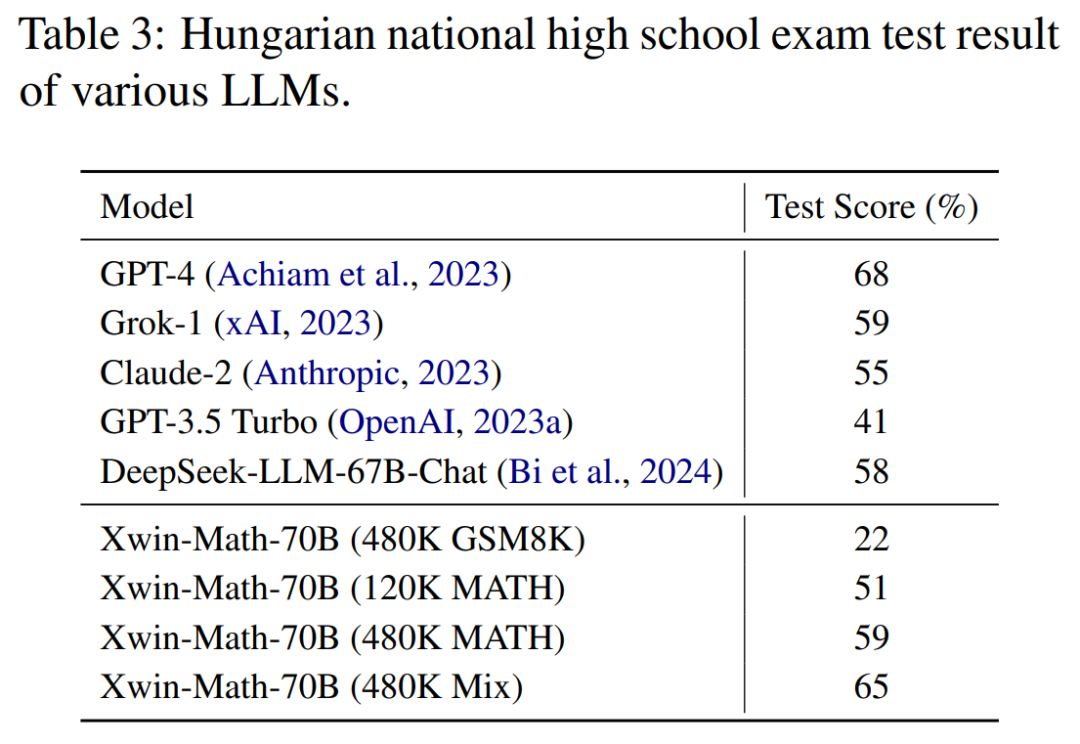

Cette étude démontre non seulement l'efficacité des données synthétiques dans l'expansion des données SFT, mais offre également une nouvelle perspective sur la recherche de grands modèles de langage dans les capacités de raisonnement mathématique. L'équipe de recherche a déclaré que leurs travaux jetaient les bases d'explorations et de progrès futurs dans ce domaine, et espérait promouvoir l'intelligence artificielle afin de réaliser de plus grandes percées dans la résolution de problèmes mathématiques. Avec les progrès continus de la technologie de l’intelligence artificielle, nous avons des raisons de nous attendre à ce que l’IA soit encore plus performante dans le domaine des mathématiques et aide davantage les humains à résoudre des problèmes mathématiques complexes. L'article couvre également les résultats des expériences d'ablation et d'autres indicateurs d'évaluation de la méthode de synthèse des données. Veuillez vous référer au texte intégral pour plus de détails. Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!