Maison >Périphériques technologiques >IA >La pierre angulaire d'AI4Science : le réseau neuronal à graphes géométriques, la revue la plus complète est ici ! L'Université Renmin de Chine Hillhouse a publié conjointement le laboratoire Tencent AI, l'Université Tsinghua, Stanford, etc.
La pierre angulaire d'AI4Science : le réseau neuronal à graphes géométriques, la revue la plus complète est ici ! L'Université Renmin de Chine Hillhouse a publié conjointement le laboratoire Tencent AI, l'Université Tsinghua, Stanford, etc.
- 王林avant
- 2024-03-07 21:10:13948parcourir

Éditeur | XS
Nature a publié deux résultats de recherche importants en novembre 2023 : la technologie de synthèse des protéines Chroma et la méthode de conception de matériaux cristallins GNoME. Les deux études ont adopté les réseaux de neurones graphiques comme outil de traitement des données scientifiques.
En fait, les réseaux de neurones graphiques, en particulier les réseaux de neurones graphes géométriques, ont toujours été un outil important pour la recherche en intelligence scientifique (AI for Science). En effet, les systèmes physiques tels que les particules, les molécules, les protéines et les cristaux dans le domaine scientifique peuvent être modélisés dans une structure de données spéciale : des graphiques géométriques.
Différents des diagrammes topologiques généraux, afin de mieux décrire le système physique, les diagrammes géométriques ajoutent des informations spatiales indispensables et doivent respecter la symétrie physique de translation, de rotation et de retournement. Compte tenu de la supériorité des réseaux neuronaux à graphes géométriques pour la modélisation des systèmes physiques, diverses méthodes ont vu le jour ces dernières années et le nombre d'articles continue de croître.
Récemment, l'Université Renmin de Chine Hillhouse s'est associée au Tencent AI Lab, à l'Université Tsinghua, à Stanford et à d'autres institutions pour publier un article de synthèse : "Une enquête sur les réseaux neuronaux à graphes géométriques : structures de données, modèles et applications". Basée sur une brève introduction aux connaissances théoriques telles que la théorie des groupes et la symétrie, cette revue passe systématiquement en revue la littérature pertinente sur les réseaux neuronaux à graphes géométriques, depuis les structures de données et les modèles jusqu'à de nombreuses applications scientifiques.

Lien papier :https://arxiv.org/abs/2403.00485
Lien GitHub :https://github.com/RUC-GLAD/GGNN4Science
Dans cette revue, l'auteur After En recherchant plus de 300 références, nous avons résumé 3 modèles de réseaux neuronaux à graphes géométriques différents, introduit des méthodes associées pour un total de 23 tâches différentes sur diverses données scientifiques telles que des particules, des molécules et des protéines, et collecté plus de 50 ensembles de données connexes. Enfin, la revue attend avec impatience les futures orientations de recherche, notamment les modèles de base de graphes géométriques, la combinaison avec de grands modèles de langage, etc.
Ce qui suit est une brève introduction à chaque chapitre.
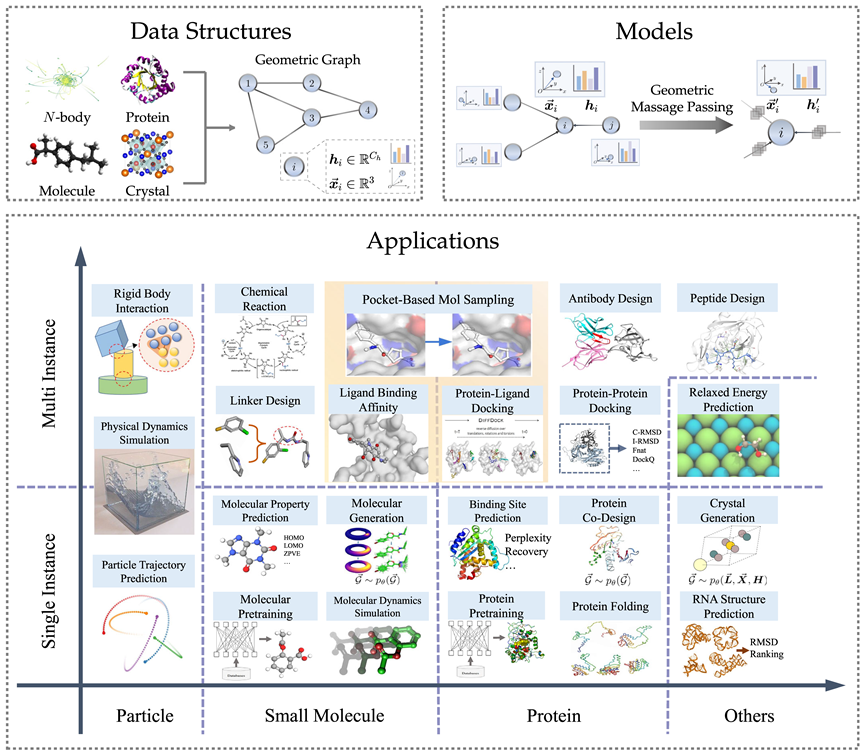
Structure de données du graphique géométrique
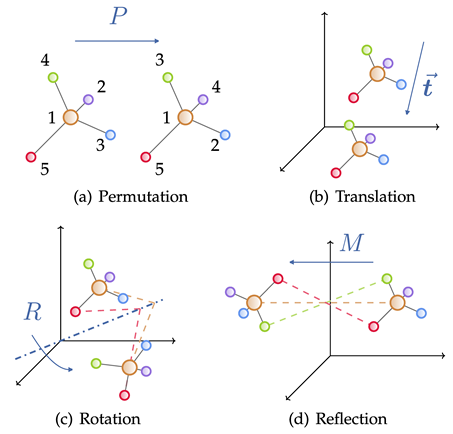
Le graphique géométrique se compose d'une matrice de contiguïté, des caractéristiques des nœuds et des informations géométriques des nœuds (telles que les coordonnées). Dans l'espace euclidien, les figures géométriques montrent généralement des symétries physiques de translation, de rotation et de réflexion. Des groupes sont généralement utilisés pour décrire ces transformations, notamment le groupe euclidien, le groupe de translation, le groupe orthogonal, le groupe de permutation, etc. Intuitivement, cela peut être compris comme une combinaison de quatre opérations : déplacement, translation, rotation et retournement dans un certain ordre.
Pour de nombreux domaines de l'IA pour la science, les graphiques géométriques constituent une méthode de représentation puissante et polyvalente, qui peut être utilisée pour représenter de nombreux systèmes physiques, notamment de petites molécules, des protéines, des cristaux, des nuages de points physiques, etc.
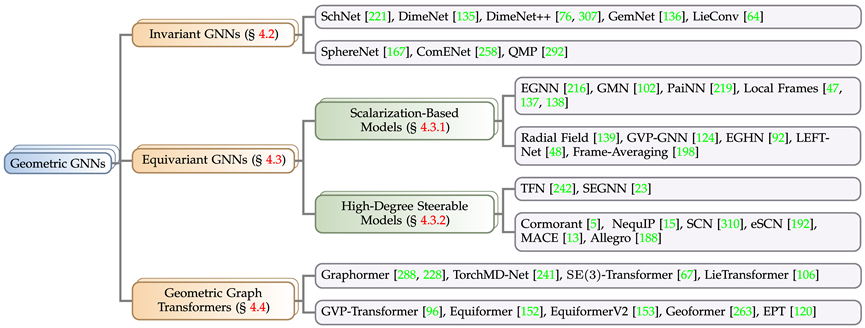
Modèle de réseau neuronal à graphe géométrique
Selon les exigences de symétrie des objectifs de solution dans des problèmes réels, cet article divise les réseaux de neurones à graphe géométrique en trois catégories : le modèle invariant et le modèle de modèle équivariant, et le transformateur de graphe géométrique inspiré de l'architecture Transformer. Le modèle équivariant est subdivisé en un modèle basé sur la scalarisation et un modèle orientable à haut degré basé sur l'harmonisation sphérique. Selon les règles ci-dessus, l'article rassemble et catégorise les modèles de réseaux neuronaux à graphes géométriques bien connus de ces dernières années.
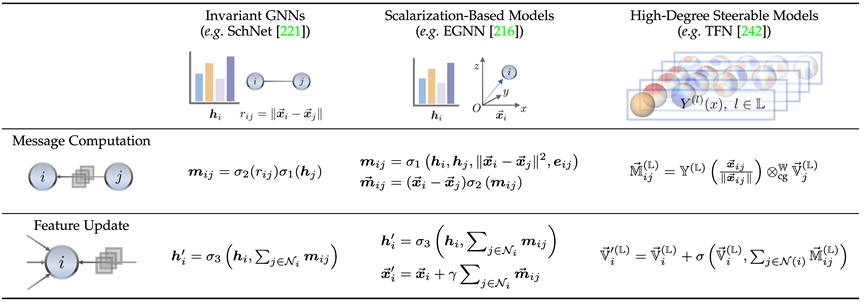
Ici, nous introduisons brièvement la relation entre le modèle invariant (SchNet[1]), le modèle de méthode de scalarisation (EGNN[2]) et le modèle contrôlable d'ordre élevé (TFN[3]) à travers le travail représentatif de chaque branche et différence. On peut constater que tous les trois utilisent des mécanismes de transmission de messages, mais que les deux derniers, qui sont des modèles équivariants, introduisent une transmission de message géométrique supplémentaire.
Le modèle invariant utilise principalement les caractéristiques du nœud lui-même (telles que le type d'atome, la masse, la charge, etc.) et les caractéristiques invariantes entre les atomes (telles que la distance, l'angle [4], l'angle dièdre [5]), etc. .pour calculer les messages.
En plus de cela, la méthode de scalarisation introduit en outre des informations géométriques via la différence de coordonnées entre les nœuds et combine linéairement les informations invariantes en tant que poids des informations géométriques pour obtenir l'introduction de l'équivariance.
Les modèles contrôlables d'ordre élevé utilisent des harmoniques sphériques d'ordre élevé et des matrices de Wigner-D pour représenter les informations géométriques du système. Cette méthode contrôle l'ordre de représentation irréductible via le coefficient Clebsch-Gordan en mécanique quantique, réalisant ainsi le passage du message géométrique. processus.
La précision du réseau neuronal du graphe géométrique est grandement améliorée grâce à la symétrie garantie par ce type de conception, et elle brille également dans la tâche de génération.
La figure ci-dessous montre les résultats des trois tâches de prédiction des propriétés moléculaires, d'amarrage protéine-ligand et de conception (génération) d'anticorps à l'aide du réseau neuronal à graphe géométrique et du modèle traditionnel sur les trois ensembles de données de QM9, PDBBind et SabDab It. On voit clairement que Avantages des réseaux de neurones à graphes géométriques.
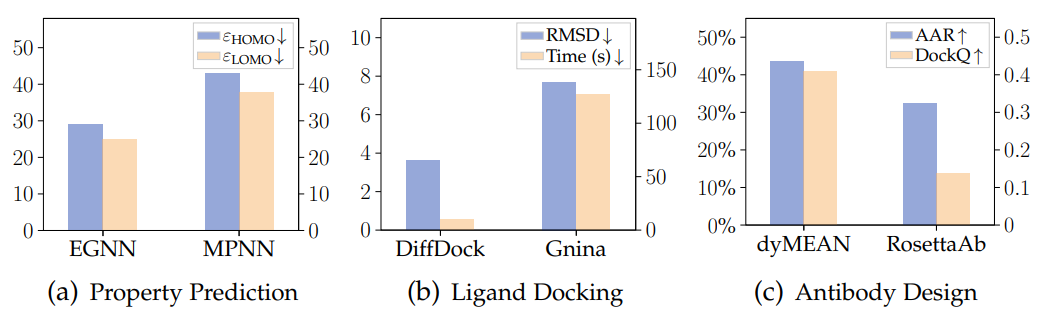
Applications scientifiques
En termes d'applications scientifiques, la revue couvre la physique (particules), la biochimie (petites molécules, protéines) et d'autres scénarios d'application tels que les cristaux, les définitions de tâches et les garanties de symétrie requises. À partir des catégories , les ensembles de données couramment utilisés dans chaque tâche et les idées classiques de conception de modèles dans ce type de tâches sont introduits.
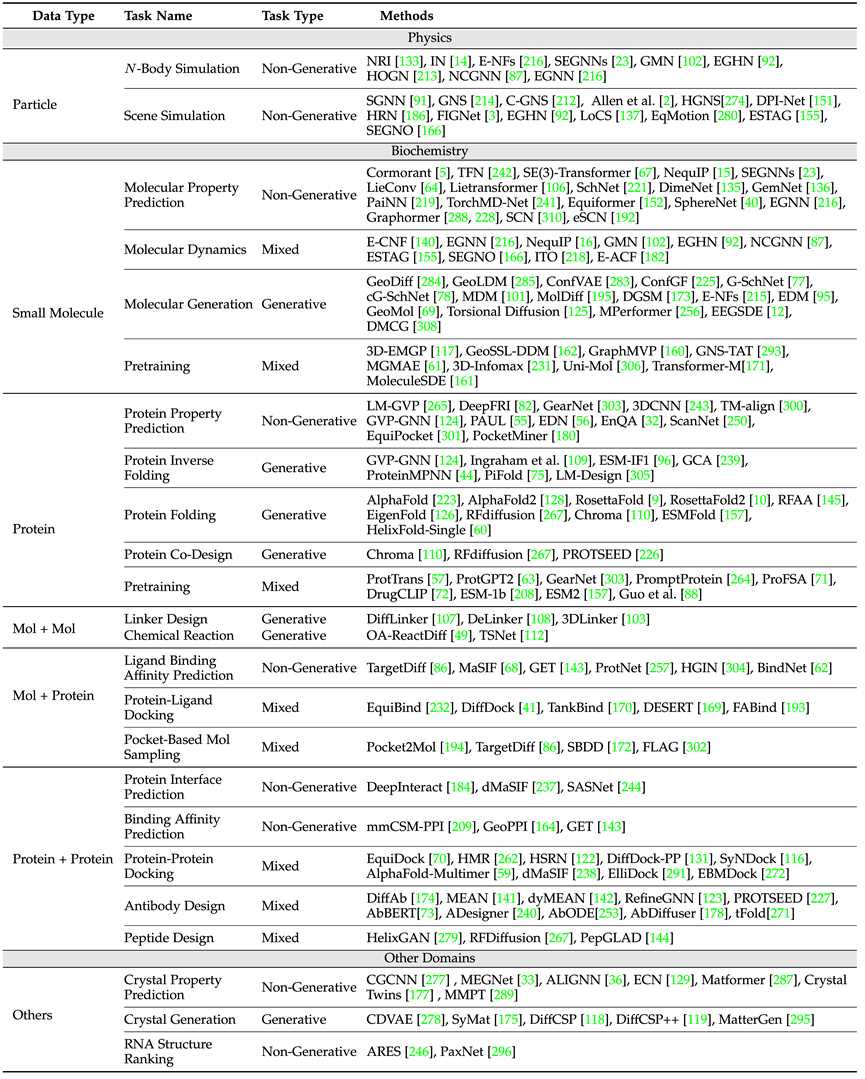
Le tableau ci-dessus présente les tâches courantes et les modèles classiques dans divers domaines. Parmi eux, selon une instance unique et des instances multiples (telles que les réactions chimiques, qui nécessitent la participation de plusieurs molécules), l'article distingue séparément les petites molécules - petites molécules, petites molécules -Protéine, protéine - trois domaines de protéines.
Afin de mieux faciliter la conception de modèles et le développement d'expériences sur le terrain, l'article compte les ensembles de données et les références communs pour deux types de tâches basées sur une instance unique et des instances multiples, et enregistre les tailles d'échantillon et les types de tâches de différents ensembles de données. .
Le tableau suivant résume les ensembles de données de tâches à instance unique courants.
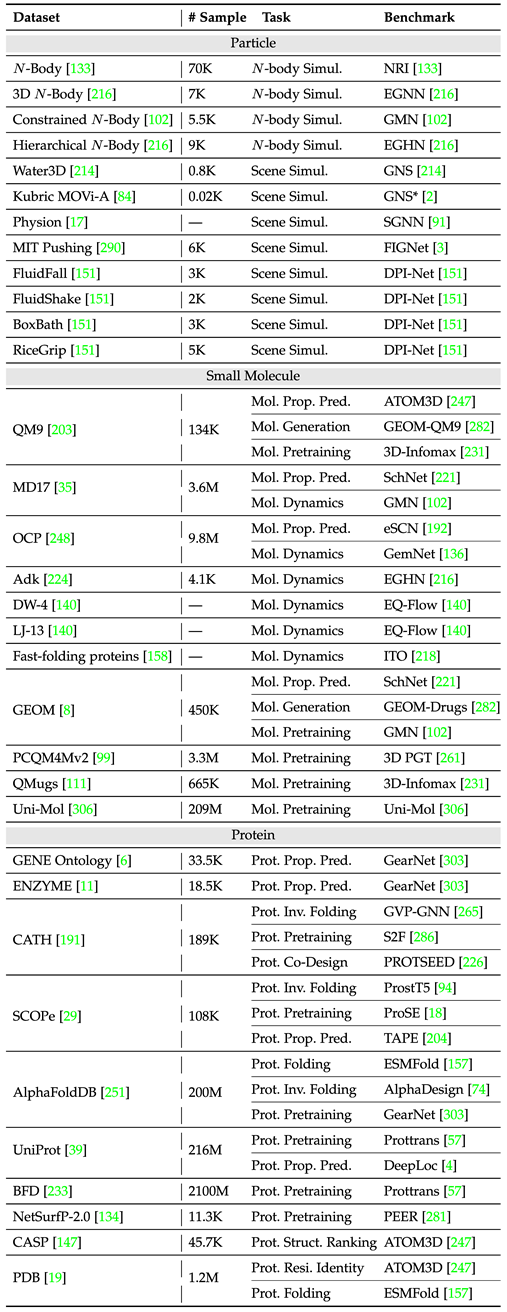
Le tableau suivant organise les ensembles de données de tâches multi-instances courantes.
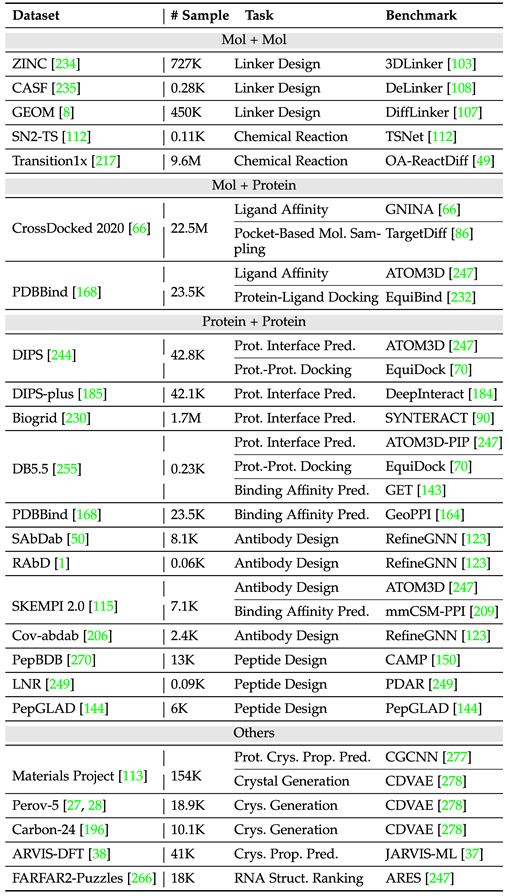
Perspectives futures
L'article donne un aperçu préliminaire de plusieurs aspects, dans l'espoir de servir de point de départ :
1. Le modèle de graphe géométrique de base
est unifié dans diverses tâches et domaines. La supériorité du modèle de base s'est pleinement reflétée dans les progrès significatifs des modèles de la série GPT. Comment réaliser une conception raisonnable dans l'espace des tâches, l'espace des données et l'espace des modèles, afin d'introduire cette idée dans la conception du réseau neuronal à graphes géométriques, reste un problème ouvert intéressant.
2. Cycle efficace de formation de modèles et de vérification expérimentale dans le monde réel
L'acquisition de données scientifiques est coûteuse et prend du temps, et les modèles qui ne sont évalués que sur des ensembles de données indépendants ne peuvent pas refléter directement les commentaires du monde réel. L'importance de parvenir à des paradigmes expérimentaux itératifs modèles-réalité efficaces similaires à GNoME (qui intègre un pipeline de bout en bout comprenant une formation sur les réseaux de graphes, des calculs de théorie fonctionnelle de la densité et des laboratoires automatisés pour la découverte et la synthèse des matériaux) augmentera de jour en jour. jour.
3. Intégration avec les grands modèles de langage (LLM)
Il a été largement prouvé que les grands modèles de langage (LLM) possèdent des connaissances riches, couvrant divers domaines. Bien que certains travaux utilisent les LLM pour certaines tâches telles que la prédiction des propriétés moléculaires et la conception de médicaments, ils ne fonctionnent que sur des primitives ou des graphes moléculaires. Comment les combiner de manière organique avec des réseaux neuronaux de graphes géométriques afin qu'ils puissent traiter des informations structurelles 3D et effectuer des prédictions ou des générations sur des structures 3D reste encore un défi.
4. Assouplissement des contraintes d'équivariance
Il ne fait aucun doute que l'équivariance est cruciale pour améliorer l'efficacité des données et la capacité de généralisation du modèle, mais il convient de noter que des contraintes d'équivariance trop fortes peuvent parfois trop restreindre le modèle. performance. Par conséquent, comment équilibrer l’équivariance et l’adaptabilité du modèle conçu est une question très intéressante. L'exploration dans ce domaine peut non seulement enrichir notre compréhension du comportement des modèles, mais également ouvrir la voie au développement de solutions plus robustes et générales avec une applicabilité plus large.
Références
[1] Schütt K, Kindermans PJ, Sauceda Felix H E, et al. Schnet : Un réseau neuronal convolutionnel à filtre continu pour la modélisation des interactions quantiques [J]. .
[2] Satorras V G, Hoogeboom E, Welling M. E (n) réseaux de neurones à graphes équivariants[C]//Conférence internationale sur l'apprentissage automatique. PMLR, 2021 : 9323-9332.
[3] Thomas N, Smidt T, Kearnes S, et al. Réseaux de champs tensoriels : réseaux de neurones équivariants en rotation et en translation pour les nuages de points 3D [J]. Préimpression arXiv arXiv:1802.08219, 2018.
[4] Gasteiger J, Groß J, Günnemann S. Transmission de messages directionnels pour les graphiques moléculaires[C]//Conférence internationale sur les représentations d'apprentissage. 2019.
[5] Gasteiger J, Becker F, Günnemann S. Gemnet : Réseaux neuronaux à graphes directionnels universels pour molécules[J]. Advances in Neural Information Processing Systems, 2021, 34 : 6790-6802.
[6] Merchant A, Batzner S, Schoenholz SS, et al. Mise à l'échelle de l'apprentissage profond pour la découverte des matériaux[J]. Nature, 2023, 624(7990) : 80-85.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Parlons de la théorie de la réplication maître-esclave, de la sentinelle et du clustering dans Redis [explication détaillée avec images et texte]
- Le modèle de langage IA open source de Meta, MusicGen, peut convertir du texte et des mélodies en morceaux de musique complets.
- Le talent visuel des grands modèles de langage : GPT peut également résoudre des tâches visuelles grâce à l'apprentissage contextuel

