Résumé de sept techniques de réduction de dimensionnalité linéaire couramment utilisées dans l'apprentissage automatique

Dans l'article précédent, nous avons principalement résumé les techniques de réduction de dimensionnalité non linéaire. Dans cet article, nous résumerons les techniques courantes de réduction de dimensionnalité linéaire.

1. Analyse en composantes principales (ACP)

L'ACP est une technique de réduction de dimensionnalité largement utilisée qui peut convertir des ensembles de données de grande dimension en représentations de basse dimension plus gérables tout en conservant les caractéristiques clés des données. En identifiant les directions (composantes principales) présentant la plus grande variance dans les données, PCA peut projeter les données dans ces directions pour atteindre l'objectif de réduction de dimensionnalité.

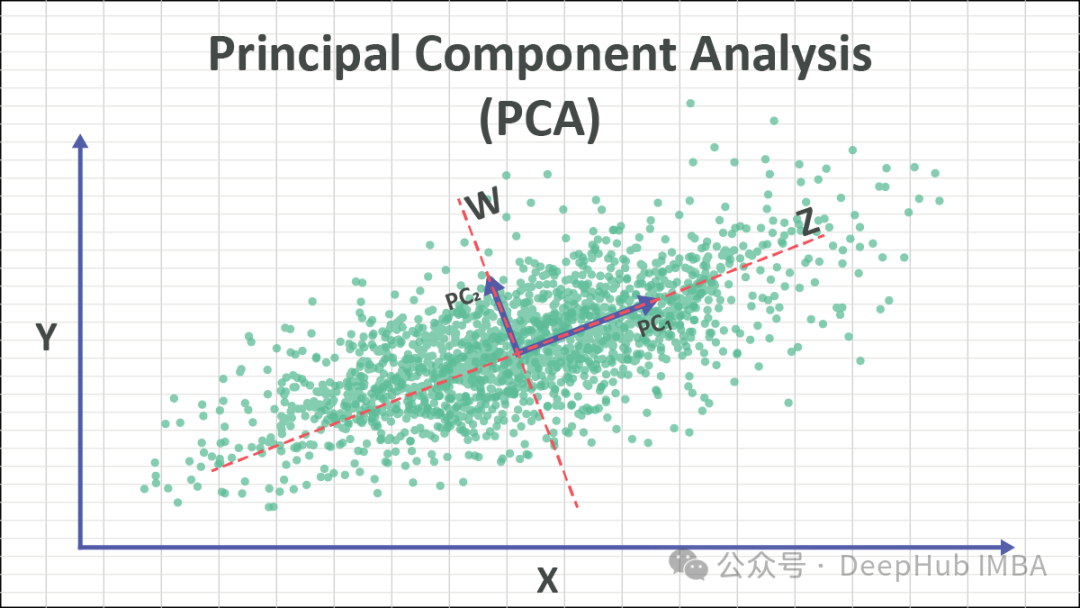
L'idée principale de PCA est de transformer les données originales en un nouveau système de coordonnées pour maximiser la variance des données. Ces nouveaux axes sont appelés composants principaux et sont des combinaisons linéaires des caractéristiques d'origine. Conserver la composante principale avec la plus grande variance conserve essentiellement les informations clés des données. En supprimant les composantes principales présentant des variances plus faibles, l’objectif de réduction de dimensionnalité peut être atteint.

Les étapes de la PCA sont les suivantes :

1. Standardiser les données : normaliser les données d'origine afin que la moyenne de chaque caractéristique soit de 0 et la variance de 1.
2. Calculer la matrice de covariance : calculez la matrice de covariance des données standardisées.
3. Calculer les valeurs propres et les vecteurs propres : effectuez une décomposition des valeurs propres sur la matrice de covariance pour obtenir les valeurs propres et les vecteurs propres correspondants.
4. Sélectionnez les composantes principales : sélectionnez les k vecteurs propres supérieurs comme composantes principales en fonction de la taille des valeurs propres, où k est la dimension après réduction de dimensionnalité.
5. Données de projection : projetez les données originales sur les composants principaux sélectionnés pour obtenir un ensemble de données dimensionnellement réduit.

PCA peut être utilisé pour des tâches telles que la réduction de la dimensionnalité des données, l'extraction de caractéristiques et la reconnaissance de formes. Lorsque vous utilisez la PCA, vous devez vous assurer que les données répondent à l'hypothèse de base de séparabilité linéaire, et effectuer le prétraitement et la compréhension des données nécessaires pour obtenir des effets de réduction de dimensionnalité précis.

2. Analyse factorielle (FA)

L'analyse factorielle (FA) est une technique statistique utilisée pour identifier la structure ou les facteurs sous-jacents parmi les variables observées. Elle vise à découvrir les facteurs latents qui expliquent la variance partagée entre les variables observées. en fin de compte, les réduisant à un plus petit nombre de variables non liées.

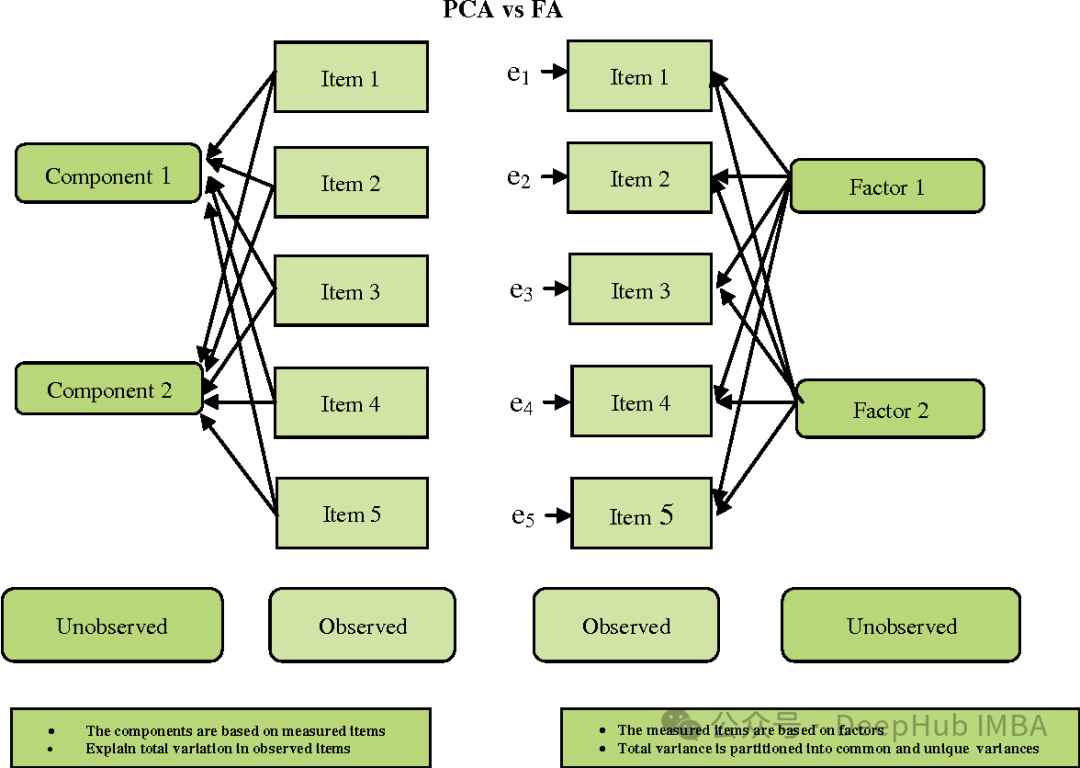
FA et PCA sont quelque peu similaires, mais il existe quelques différences importantes :

1. Objectif : PCA vise à trouver la direction de la variance maximale, tandis que FA vise à trouver les variables (facteurs) sous-jacentes qui expliquent la variation commune observée entre les variables.
2. Hypothèses : PCA suppose que les variables observées sont les caractéristiques originales observées, tandis que FA suppose que les variables observées sont la somme de combinaisons linéaires de facteurs latents et d'erreurs aléatoires.
3. Interprétabilité : la PCA a tendance à être plus simple car ses principaux composants sont des combinaisons linéaires des fonctionnalités d'origine. Et les facteurs de FA peuvent être moins faciles à interpréter car il s’agit de combinaisons linéaires de variables observées plutôt que de caractéristiques brutes.
4. Rotation : En FA, les facteurs subissent souvent une rotation pour les rendre plus faciles à interpréter.

L'analyse factorielle est largement utilisée dans des domaines tels que la psychologie, les sciences sociales et les études de marché. Il permet de simplifier les ensembles de données, de découvrir les structures sous-jacentes et de réduire les erreurs de mesure. Cependant, il faut être prudent lors de la sélection du nombre de facteurs et de la méthode de rotation pour garantir que les résultats sont interprétables et valides.

3. Analyse discriminante linéaire, LDA

L'analyse discriminante linéaire (LDA) est une technologie d'apprentissage supervisé pour la réduction de dimensionnalité et l'extraction de caractéristiques. Elle diffère de l'analyse en composantes principales (ACP) car elle prend en compte non seulement la structure de variance des données, mais également les informations sur les catégories des données. LDA vise à trouver une direction de projection qui maximise la distance entre les différentes catégories (diffusion inter-classe) tout en minimisant la distance au sein d'une même catégorie (diffusion intra-classe).

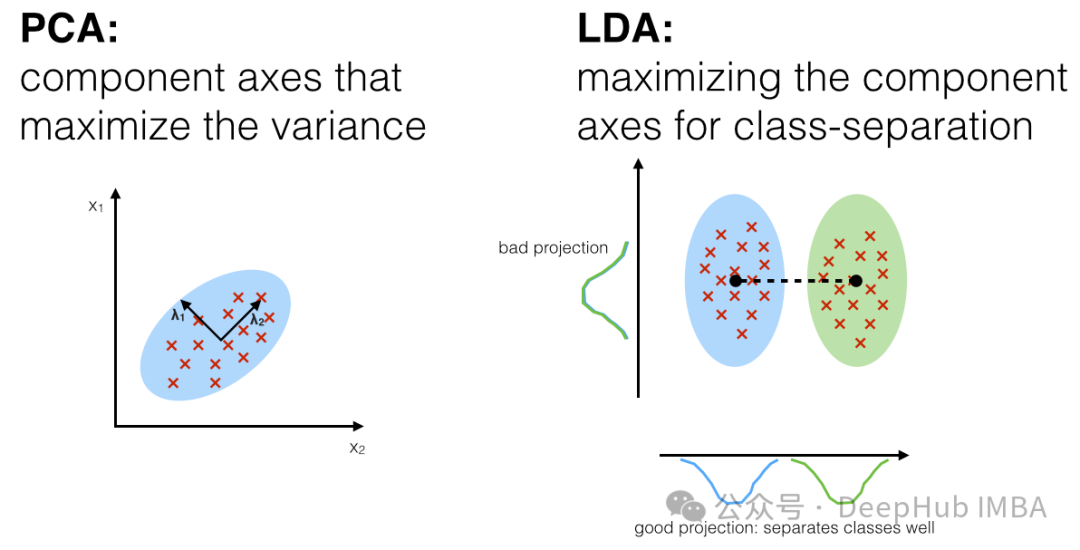
Les principales étapes de LDA sont les suivantes :

1. Calculez le vecteur moyen de la catégorie : pour chaque catégorie, calculez le vecteur moyen de tous les échantillons de cette catégorie.
2. Calculez la matrice de dispersion au sein de la classe : pour chaque catégorie, calculez la matrice de dispersion entre tous les échantillons de la catégorie et son vecteur moyen, et additionnez-les.
3. Calculez la matrice de dispersion entre les classes : calculez la matrice de dispersion entre les vecteurs moyens de toutes les catégories et le vecteur moyen global.
4. Calculer les valeurs propres et les vecteurs propres : multipliez la matrice inverse de la matrice par la matrice de dispersion inter-classes et effectuez une décomposition des valeurs propres de la matrice résultante pour obtenir les valeurs propres et les vecteurs propres.
5. Sélectionnez la direction de projection : sélectionnez les k vecteurs propres supérieurs avec les valeurs propres les plus grandes comme direction de projection, où k est la dimension après réduction de dimensionnalité.
6. Données de projection : projetez les données originales dans la direction de projection sélectionnée pour obtenir les données dimensionnellement réduites.

L'avantage de LDA est qu'il prend en compte les informations de catégorie des données, afin que la projection générée puisse mieux distinguer les différences entre les différentes catégories. Il est largement utilisé dans la reconnaissance de formes, la reconnaissance faciale, la reconnaissance vocale et d'autres domaines. LDA peut rencontrer certains problèmes lorsqu’il s’agit de classes multiples et de déséquilibres de classes, et nécessite une attention particulière.

4. Eigendecomposition

Eigendecomposition (décomposition des valeurs propres) est une technique mathématique utilisée pour décomposer des matrices carrées. Il décompose une matrice carrée en un ensemble de vecteurs propres et le produit de valeurs propres. Les vecteurs propres représentent des directions qui ne changent pas de direction pendant les transformations, tandis que les valeurs propres représentent une mise à l'échelle le long de ces directions pendant les transformations.

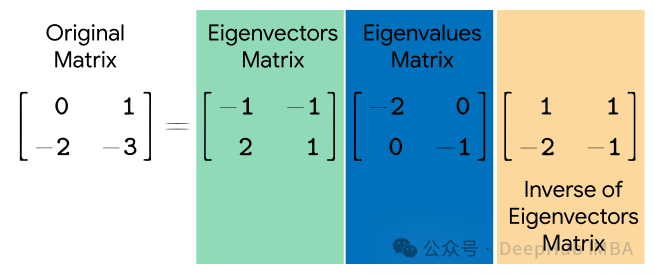
Étant donné une matrice carrée AA, sa décomposition en valeurs propres s'exprime comme suit :

où, Q est une matrice composée de vecteurs propres de A, Λ est une matrice diagonale et les éléments sur sa diagonale sont la valeur propre de A.

La décomposition des valeurs propres a de nombreuses applications, notamment l'analyse en composantes principales (ACP), la reconnaissance des faces propres, le regroupement spectral, etc. En PCA, la décomposition des valeurs propres est utilisée pour trouver les vecteurs propres de la matrice de covariance des données et donc les principales composantes des données. Dans le clustering spectral, la décomposition des valeurs propres est utilisée pour trouver les vecteurs propres de la carte de similarité, effectuant ainsi le clustering. La reconnaissance des visages propres utilise la décomposition des valeurs propres pour identifier les caractéristiques importantes des images de visage.

Bien que la décomposition des valeurs propres soit très utile dans de nombreuses applications, toutes les matrices carrées ne peuvent pas être décomposées en valeurs propres. Par exemple, les matrices singulières ou les matrices non carrées ne peuvent pas être décomposées en valeurs propres. La décomposition des valeurs propres peut prendre beaucoup de temps à calculer sur de grandes matrices.

5. Décomposition en valeurs singulières (SVD)

La décomposition en valeurs singulières (SVD) est une technique importante pour la décomposition matricielle. Il décompose une matrice en produit de trois matrices, qui sont la transposée d'une matrice orthogonale, d'une matrice diagonale et d'une autre matrice orthogonale.

Étant donné une matrice m × n AA, sa décomposition en valeurs singulières est exprimée comme suit :

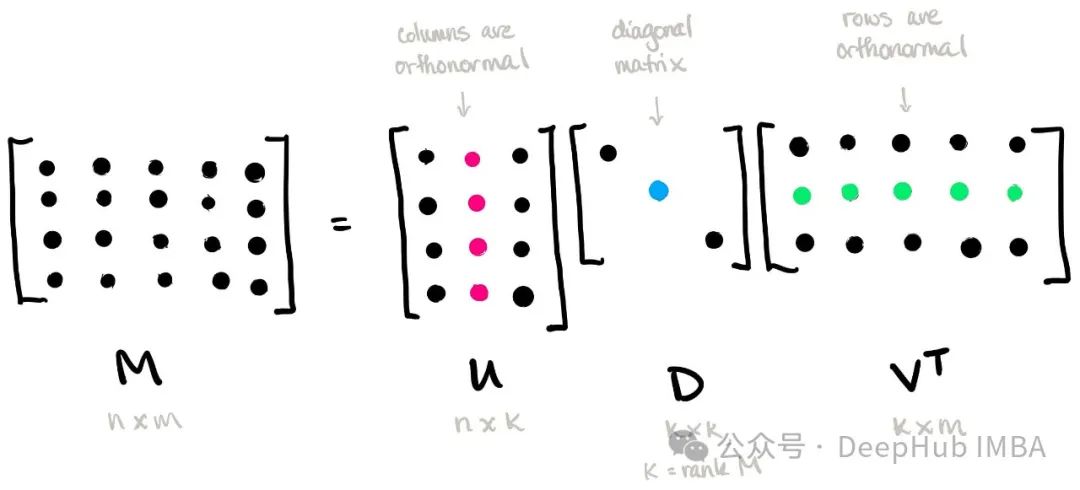
où, U est une matrice orthogonale m × m, appelée matrice vectorielle singulière gauche Σ est une matrice diagonale m × n ; , et les éléments sur sa diagonale sont appelés valeurs singulières ; VT est la transposée d'une matrice orthogonale n × n, appelée matrice vectorielle singulière droite.

La décomposition en valeurs singulières a un large éventail d'applications, notamment la compression de données, la réduction de dimensionnalité, la solution matricielle inverse, le système de recommandation, etc. Dans la réduction de dimensionnalité, seuls les éléments avec des valeurs singulières plus grandes sont conservés, ce qui permet d'obtenir une compression et une représentation efficaces des données. Dans les systèmes de recommandation, la relation entre les utilisateurs et les éléments peut être modélisée via une décomposition en valeurs singulières pour fournir des recommandations personnalisées.

La décomposition en valeurs singulières peut également être utilisée pour résoudre les inverses de matrice, en particulier pour les matrices singulières. En conservant les termes avec des valeurs singulières plus grandes, la matrice inverse peut être résolue approximativement, évitant ainsi le problème de l'inversion de la matrice singulière.

6. Décomposition en valeurs singulières tronquées (TSVD)

La décomposition en valeurs singulières tronquées (TSVD) est une variante de la décomposition en valeurs singulières (SVD), qui conserve uniquement les sommes de valeurs singulières les plus importantes dans le calcul des vecteurs singuliers correspondants, atteignant ainsi la dimensionnalité. réduction et compression des données.

Étant donné une matrice AA m × n, sa décomposition en valeurs singulières tronquées est exprimée comme suit :

où, Uk est une matrice orthogonale m × k, Σk est une matrice diagonale k × k, VkT est la transposée d'un k × n matrice orthogonale qui correspond à conserver les k valeurs singulières les plus importantes et les vecteurs singuliers correspondants.

Le principal avantage du TSVD est qu'il peut réaliser une réduction de dimensionnalité et une compression des données en conservant les valeurs singulières et les vecteurs singuliers les plus importants, réduisant ainsi les coûts de stockage et de calcul. Ceci est particulièrement utile lorsque vous travaillez avec des ensembles de données à grande échelle, car l'espace de stockage et le temps de calcul requis peuvent être considérablement réduits.

TSVD a des applications dans de nombreux domaines, notamment le traitement d'images, le traitement du signal, les systèmes de recommandation, etc. Dans ces applications, TSVD peut être utilisé pour réduire la dimensionnalité des données, supprimer le bruit, extraire des fonctionnalités clés, etc.

7. Factorisation matricielle non négative (NMF)

La factorisation matricielle non négative (NMF) est une technologie de décomposition de données et de réduction de dimensionnalité. Sa caractéristique est que les matrices et les vecteurs obtenus par décomposition sont non négatifs. Cela rend NMF utile dans de nombreuses applications, en particulier dans des domaines tels que l'exploration de texte, le traitement d'images et les systèmes de recommandation.

Étant donné une matrice non négative VV, NMF la décompose sous la forme du produit de deux matrices non négatives WW et HH :

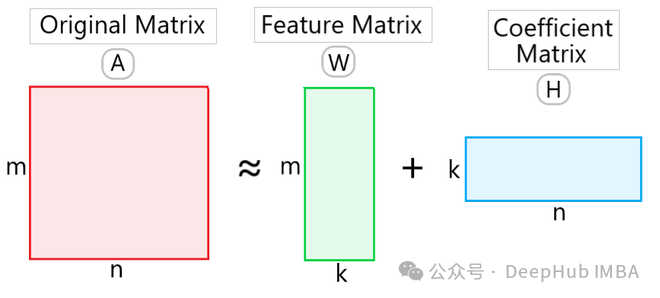
où W est une matrice non négative de m × k, appelée matrice de base (matrice de base) ou matrice de caractéristiques, H est une matrice k × n non négative, appelée matrice de coefficients. Ici k est la dimension après réduction de dimensionnalité.

L'avantage du NMF est qu'il peut obtenir des résultats de décomposition ayant une signification physique car tous les éléments sont non négatifs. Cela permet à NMF de découvrir des sujets latents dans l'exploration de texte et d'extraire les caractéristiques des images lors du traitement d'images. De plus, NMF a également pour fonction de réduire la dimensionnalité des données, ce qui peut réduire la dimensionnalité et l'espace de stockage des données.

Les applications NMF incluent la modélisation de sujets de texte, la segmentation et la compression d'images, le traitement du signal audio, les systèmes de recommandation, etc. Dans ces domaines, NMF est largement utilisé dans des tâches telles que l'analyse de données et l'extraction de caractéristiques, ainsi que la récupération et la classification d'informations.

Résumé

La technologie de réduction de dimensionnalité linéaire est un type de technologie utilisé pour mapper des ensembles de données de grande dimension à un espace de faible dimension. L'idée principale est de conserver les principales caractéristiques de l'ensemble de données grâce à une transformation linéaire. Ces techniques de réduction de dimensionnalité linéaire ont leurs avantages uniques et leur applicabilité dans différents scénarios d'application, et la méthode appropriée peut être sélectionnée en fonction de la nature des données et des exigences de la tâche. Par exemple, PCA convient à la réduction non supervisée de la dimensionnalité des données, tandis que LDA convient aux tâches d'apprentissage supervisé.

Sur la base de l'article précédent, nous avons présenté 10 techniques de réduction de dimensionnalité non linéaire et 7 techniques de réduction de dimensionnalité linéaire. Faisons un résumé

Technologie de réduction de dimensionnalité linéaire : mapper les données dans un espace de faible dimension basé sur une transformation linéaire. ensembles de données ; comme dans le cas où les points de données sont distribués sur un sous-espace linéaire ; parce que son algorithme est simple, il est efficace sur le plan informatique et facile à comprendre et à mettre en œuvre, il ne peut généralement pas capturer la structure non linéaire des données, ce qui peut conduire à des informations ; est perdu.

Technologie de réduction de dimensionnalité non linéaire : mappe les données dans un espace de faible dimension via une transformation non linéaire ; convient aux ensembles de données avec des structures non linéaires, telles que des points de données distribués sur une variété ; peut mieux conserver la non-linéarité dans la structure des données et les relations locales, offrant ainsi une meilleure visualisation ; complexité informatique plus élevée, nécessitant généralement plus de ressources et de temps de calcul.

Si les données sont linéairement séparables ou si les ressources informatiques sont limitées, une technologie de réduction de dimensionnalité linéaire peut être sélectionnée. Si les données contiennent des structures non linéaires complexes ou nécessitent une meilleure visualisation, vous pouvez envisager d'utiliser une technologie de réduction de dimensionnalité non linéaire. En pratique, vous pouvez également essayer différentes méthodes et choisir la technologie de réduction de dimensionnalité la plus appropriée en fonction de l'effet réel.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!