Maison >développement back-end >Tutoriel Python >Explication détaillée de l'algorithme Bellman Ford et de sa mise en œuvre en Python
Explication détaillée de l'algorithme Bellman Ford et de sa mise en œuvre en Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2024-01-22 19:39:131279parcourir
L'algorithme Bellman Ford peut trouver le chemin le plus court entre le nœud cible et les autres nœuds dans le graphique pondéré. Ceci est très similaire à l'algorithme de Dijkstra. L'algorithme de Bellman-Ford peut gérer des graphiques avec des poids négatifs et est relativement simple en termes de mise en œuvre.
Explication détaillée du principe de l'algorithme de Bellman Ford
L'algorithme de Bellman Ford trouve de manière itérative de nouveaux chemins plus courts que les chemins surestimés en surestimant les longueurs de chemin du sommet de départ à tous les autres sommets.
Parce que nous voulons enregistrer la distance du trajet de chaque nœud, nous pouvons la stocker dans un tableau de taille n, n représente également le nombre de nœuds.
Diagramme d'instance
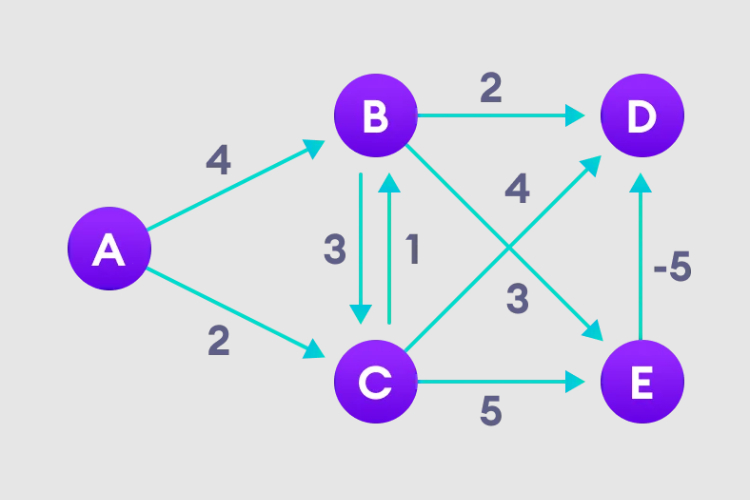
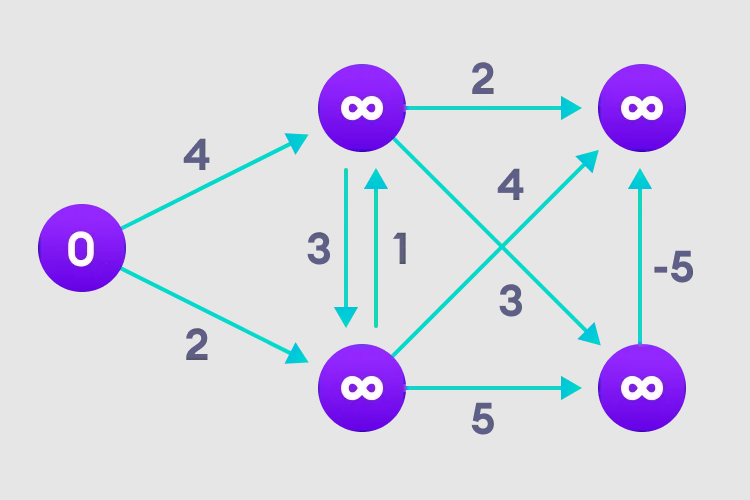
1. Sélectionnez le nœud de départ, attribuez-le à tous les autres sommets à l'infini et enregistrez la valeur du chemin.
2. Visitez chaque bord et effectuez une opération de relaxation pour mettre à jour en permanence le chemin le plus court.
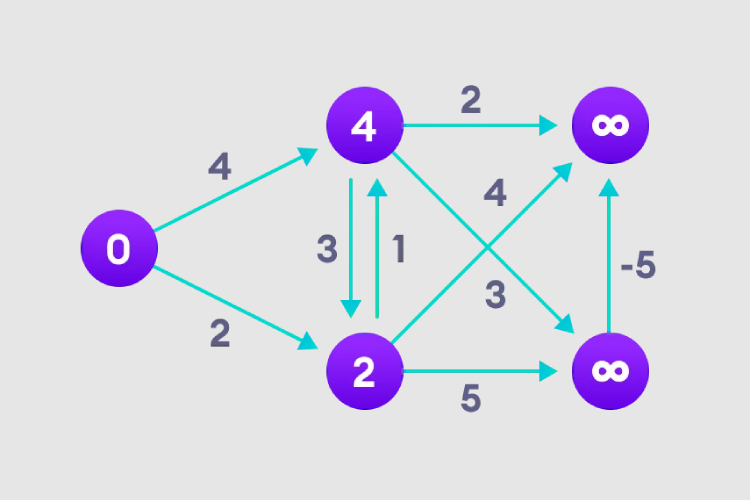
3. Nous devons faire cela N-1 fois, car dans le pire des cas, la longueur du chemin du nœud le plus court devra peut-être être réajustée N-1 fois.
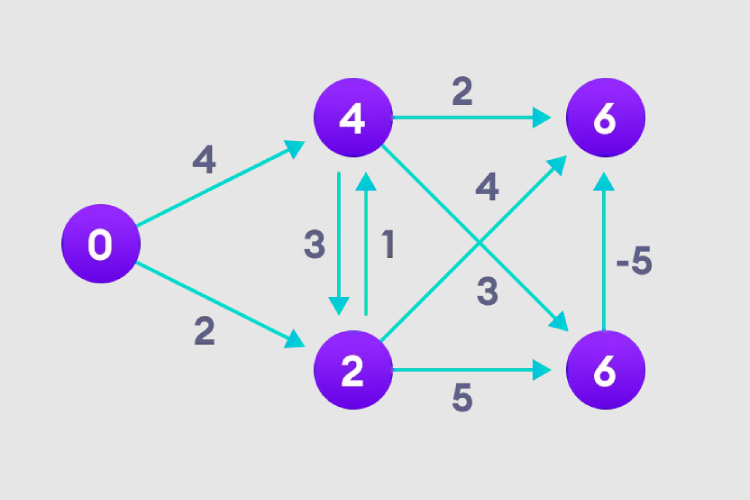
4. Remarquez comment le nœud dans le coin supérieur droit ajuste la longueur de son chemin.
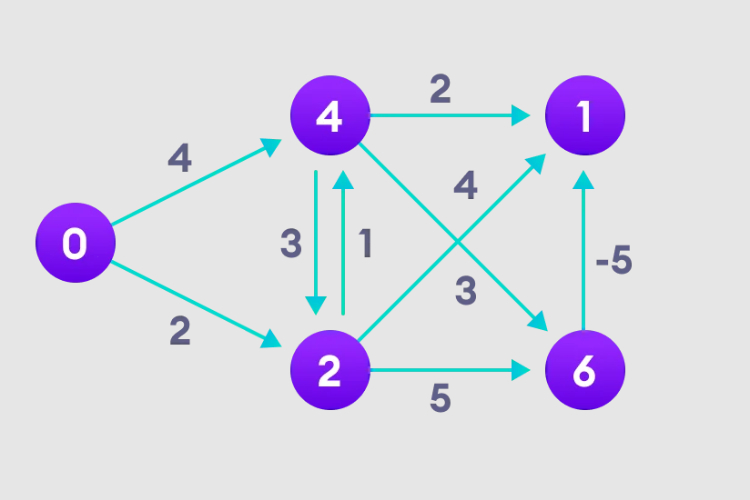
5. Une fois que tous les nœuds ont des longueurs de chemin, vérifiez s'il y a une boucle négative.
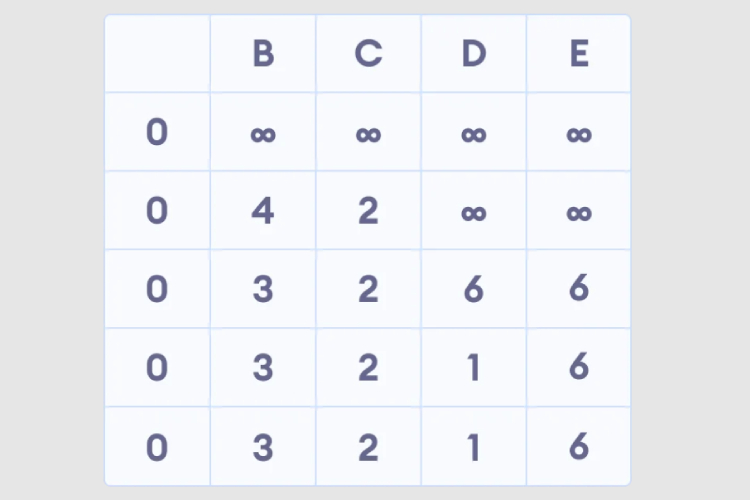
Python implémente l'algorithme Bellman Ford
class Graph:
def __init__(self, vertices):
self.V = vertices # Total number of vertices in the graph
self.graph = [] # Array of edges
def add_edge(self, s, d, w):
self.graph.append([s, d, w])
def print_solution(self, dist):
print("Vertex Distance from Source")
for i in range(self.V):
print("{0}\t\t{1}".format(i, dist[i]))
def bellman_ford(self, src):
dist = [float("Inf")] * self.V
dist[src] = 0
for _ in range(self.V - 1):
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
dist[d] = dist[s] + w
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
print("Graph contains negative weight cycle")
return
self.print_solution(dist)
g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)
g.bellman_ford(0)Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

