Maison >Périphériques technologiques >IA >Analyse approfondie des concepts et des applications des modèles de régression linéaire multiple
Analyse approfondie des concepts et des applications des modèles de régression linéaire multiple
- 王林avant
- 2024-01-22 18:30:211685parcourir
La régression linéaire multiple est la forme la plus courante de régression linéaire et est utilisée pour décrire comment une variable à réponse unique Y présente une relation linéaire avec plusieurs variables prédictives.
Exemples d'applications où la régression multiple peut être utilisée :
Le prix de vente d'une maison peut être affecté par des facteurs tels que l'emplacement, le nombre de chambres et de salles de bains, l'année de construction, la taille du terrain, etc.
2. La taille d'un enfant dépend de la taille de la mère, de la taille du père, de la nutrition et des facteurs environnementaux.
Paramètres du modèle de régression linéaire multiple
Considérons un modèle de régression linéaire multiple avec k variables prédictives indépendantes x1, x2..., xk et une variable de réponse y.
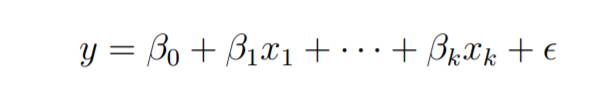
Supposons que nous ayons n observations pour k+1 variables et que n variables doivent être supérieures à k.
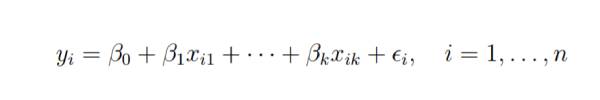
L'objectif fondamental de la régression des moindres carrés est d'ajuster l'hyperplan dans l'espace dimensionnel (k+1) pour minimiser la somme des carrés résiduels.
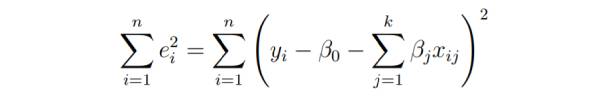
Avant de dériver les paramètres du modèle, mettez-les à zéro et dérivez l'équation normale des moindres carrés que les paramètres doivent satisfaire.
Ces équations sont formulées à l'aide de vecteurs et de matrices.

Un modèle de régression linéaire s'écrit comme suit :
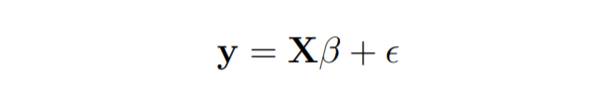
Dans la régression linéaire, le paramètre des moindres carrés estime b
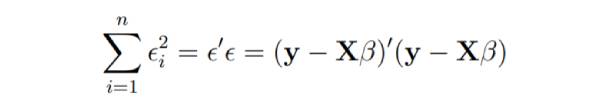
Imaginez que les colonnes des données du problème , et disons que b est variable. Nous souhaitons trouver le « meilleur » b qui minimise la somme des carrés des résidus.
La plus petite somme de carrés possible est zéro.
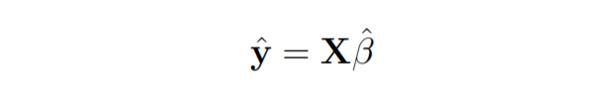
Voici le vecteur de réponse estimé.
Le code implémente une régression linéaire multiple sur l'ensemble de données data2
data2 data set
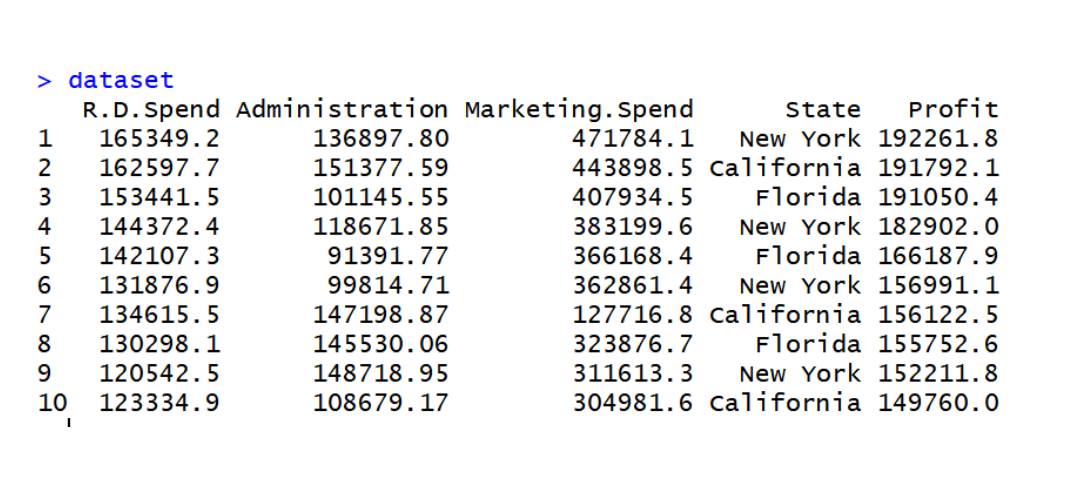
dataset=read.csv('data2.csv') dataset$State=factor(dataset$State, levels=c('New York','California','Florida'), labels=c(1,2,3)) dataset$State
library(caTools) set.seed(123) split=sample.split(dataset$Profit,SplitRatio=0.8) training_set=subset(dataset,split==TRUE) test_set=subset(dataset,split==FALSE) regressor=lm(formula=Profit~., data=training_set) y_pred=predict(regressor,newdata=test_set)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

