Implémentation d'un modèle de diffusion de suppression du bruit à l'aide de PyTorch

Avant de comprendre en détail le principe de fonctionnement du modèle probabiliste de diffusion de débruitage (DDPM), comprenons d'abord une partie du développement de l'intelligence artificielle générative, qui est également l'une des recherches fondamentales du DDPM.

VAE

VAE utilise un encodeur, un espace latent probabiliste et un décodeur. Pendant l'entraînement, l'encodeur prédit la moyenne et la variance de chaque image et échantillonne ces valeurs à partir d'une distribution gaussienne. Le résultat de l'échantillonnage est transmis au décodeur, qui convertit l'image d'entrée sous une forme similaire à l'image de sortie. La divergence KL est utilisée pour calculer la perte. Un avantage significatif de la VAE est sa capacité à générer des images diversifiées. Lors de l'étape d'échantillonnage, on peut directement échantillonner à partir de la distribution gaussienne et générer de nouvelles images via le décodeur.

GAN

Un an seulement après les auto-encodeurs variationnels (VAE), une famille révolutionnaire de modèles génératifs a émergé - les réseaux contradictoires génératifs (GAN), marquant une nouvelle classe de modèles génératifs. Le début du modèle, caractérisé par le La collaboration de deux réseaux de neurones : un générateur et un discriminateur, implique un processus de formation contradictoire. Le but du générateur est de générer des données réelles, telles que des images, à partir de bruit aléatoire, tandis que le discriminateur s'efforce de distinguer les données réelles des données générées. Tout au long de la phase de formation, le générateur et le discriminateur améliorent continuellement leurs capacités grâce à un processus d'apprentissage compétitif. Le générateur génère des données de plus en plus convaincantes, devenant ainsi plus intelligent que le discriminateur, ce qui améliore sa capacité à distinguer les échantillons réels des échantillons générés. Cette interaction contradictoire aboutit à ce que le générateur produise des données réalistes et de haute qualité. Lors de la phase d'échantillonnage, après la formation GAN, le générateur génère de nouveaux échantillons en entrant du bruit aléatoire. Il convertit ce bruit en données qui reflètent généralement des exemples réels.

Pourquoi avons-nous besoin d'une autre architecture de modèle

Bien que les GAN et les VAE aient chacun leurs propres avantages en matière de génération d'images, ils ont tous deux quelques problèmes. Les GAN peuvent générer des images réalistes très similaires aux images de l'ensemble de formation, mais leurs résultats générés manquent de diversité. Les VAE peuvent créer une variété d’images, mais ont tendance à produire des images floues. Cependant, la combinaison de ces deux capacités pour créer des images à la fois très réalistes et diversifiées n’a pas réussi. Ce défi représente un obstacle important pour les chercheurs et doit être relevé. Par conséquent, l’une des futures orientations de recherche consiste à explorer comment combiner les avantages des GAN et des VAE pour obtenir une génération d’images hautement réalistes et diversifiées. Cela apportera une avancée majeure dans le domaine de la génération d’images et sera largement utilisé dans divers domaines.

Six ans après la publication de l'article du GAN et sept ans après la publication de l'article du VAE, un modèle révolutionnaire a émergé, à savoir le modèle probabiliste de diffusion de débruitage (DDPM). DDPM combine les avantages des deux domaines pour créer des images diversifiées et réalistes.

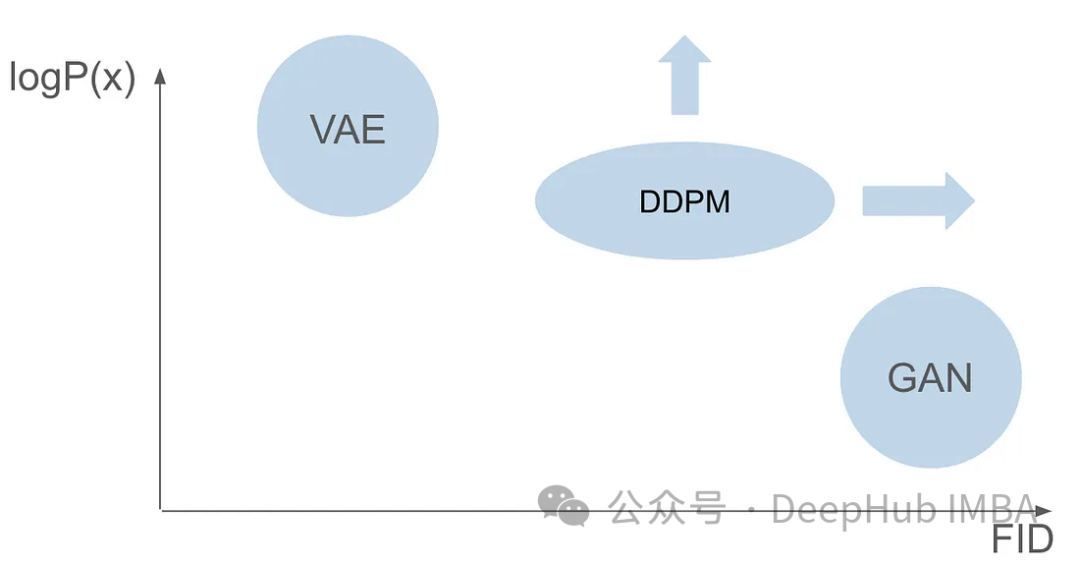
Cet article explorera la complexité du DDPM en détail, y compris le processus de formation, les processus avant et arrière et les méthodes d'échantillonnage. Nous utiliserons PyTorch pour créer et former DDPM à partir de zéro, guidant les lecteurs tout au long du processus.

Il est supposé que vous connaissez déjà les bases du deep learning et que vous disposez de bases solides en deep Computer Vision. Nous n’entrerons pas dans le détail de ces concepts de base, mais viserons plutôt à générer des images crédibles dans leur authenticité.

DDPM

Le modèle probabiliste de diffusion de débruitage (DDPM) est une méthode de pointe dans le domaine des modèles génératifs. Comparé aux modèles traditionnels qui reposent sur des fonctions de vraisemblance explicites, le DDPM fonctionne via un processus de diffusion de débruitage itératif. Ce processus consiste à ajouter progressivement du bruit à une image et à essayer de supprimer ce bruit. La théorie de base est basée sur l'idée de convertir une distribution simple (telle qu'une distribution gaussienne) en une distribution de données d'image complexe et expressive via une série d'étapes de diffusion. En d’autres termes, en transférant des échantillons de la distribution d’images originale vers une distribution gaussienne, nous pouvons construire un modèle pour inverser ce processus. Cela nous permet de partir d'une distribution entièrement gaussienne et de générer de nouvelles images avec des caractéristiques de distribution d'image, obtenant ainsi une génération d'images efficace.

La formation du DDPM se compose de deux étapes de base : un processus direct qui génère des images bruitées, fixes et non apprenables, et un processus inverse ultérieur. L’objectif principal du processus inverse est de débruiter les images à l’aide de modèles spécialisés d’apprentissage automatique.

Processus de diffusion vers l'avant

Le processus de diffusion vers l'avant est une étape fixe et impossible à apprendre, mais il nécessite certains paramètres prédéfinis. Avant de plonger dans les paramètres, comprenons d'abord comment cela fonctionne.

Le concept central de ce processus est de commencer avec une image claire. À un pas spécifique, désigné par « T », une petite quantité de bruit est progressivement introduite selon une distribution gaussienne.

Comme vous pouvez le voir sur l'image, le bruit augmente à chaque étape, approfondissons la représentation mathématique de ce bruit.

Le bruit est échantillonné à partir d'une distribution gaussienne. Pour introduire une petite quantité de bruit à chaque étape, nous utilisons une chaîne de Markov. Pour générer une image de l’horodatage actuel, nous n’avons besoin que d’une image du dernier horodatage. Le concept de chaînes de Markov est ici clé et sera crucial pour les détails mathématiques qui suivront.

Une chaîne de Markov est un processus stochastique dans lequel la probabilité de transition vers un état particulier dépend uniquement de l'état actuel et du temps écoulé, et non de la séquence d'événements précédente. Cette fonctionnalité simplifie la modélisation du processus d’ajout de bruit, facilitant ainsi son analyse mathématique.

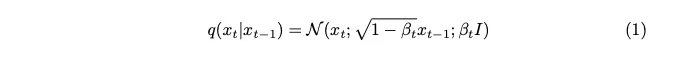
Le paramètre de variance exprimé en bêta est intentionnellement fixé à une très petite valeur afin d'introduire seulement un minimum de bruit à chaque étape.

Le paramètre de pas "T" détermine la taille de pas requise pour générer une image entièrement bruitée. Dans cet article, ce paramètre est fixé à 1 000, ce qui peut paraître important. Avons-nous vraiment besoin de créer 1 000 images bruitées pour chaque image originale de l'ensemble de données ? Il est prouvé que l'aspect chaîne de Markov aide à résoudre ce problème ? Puisque nous n’avons besoin que de l’image de l’étape précédente pour prédire l’étape suivante et que le bruit ajouté à chaque étape reste le même, nous pouvons simplifier le calcul en générant des images de bruit à des horodatages spécifiques. L'utilisation d'une technique de reparamétrage par paire nous permet de simplifier davantage les équations.

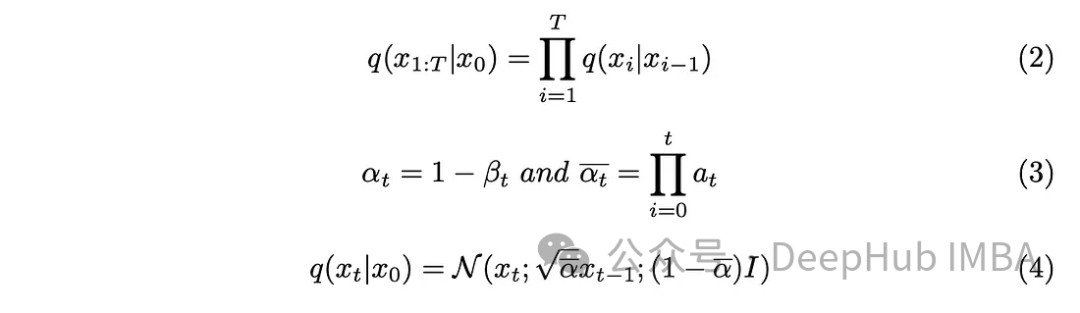
Incorporez les nouveaux paramètres introduits dans l'équation (3) dans l'équation (2), développez l'équation (2) et obtenez le résultat.

Processus de diffusion inverse

Nous avons introduit du bruit dans l'image et l'étape suivante consiste à effectuer l'opération inverse. A moins de connaître les conditions initiales, c'est-à-dire l'image non débruitée à t = 0, il est impossible de mettre en œuvre mathématiquement le processus inverse pour débruiter l'image. Notre objectif est d’échantillonner directement le bruit pour créer de nouvelles images, et ici il y a un manque d’informations sur les résultats. Je dois donc trouver un moyen de débruiter progressivement une image sans connaître le résultat. La solution est donc apparue : utiliser des modèles d’apprentissage profond pour approximer cette fonction mathématique complexe.

Avec un peu de connaissances mathématiques, le modèle se rapprochera de l'équation (5). Un détail à noter est que nous nous en tiendrons au document original du DDPM et garderons la variance fixe, bien qu'il soit également possible de faire en sorte que le modèle l'apprenne.

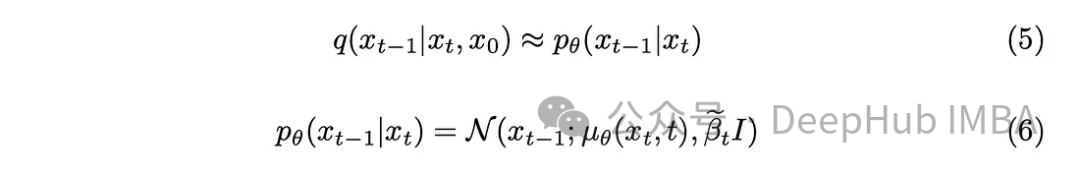
La tâche du modèle est de prédire la moyenne du bruit ajouté entre l'horodatage actuel et l'horodatage précédent. Cela peut éliminer efficacement le bruit et obtenir l'effet souhaité. Mais que se passe-t-il si notre objectif est de faire en sorte que le modèle prédise le bruit ajouté depuis « l'image originale » jusqu'au dernier horodatage ?

À moins de connaître l'image initiale sans bruit, il est mathématiquement difficile d'effectuer le processus inverse. Commençons. en définissant la variance a posteriori.

La tâche du modèle est de prédire le bruit ajouté à l'image à l'horodatage t à partir de l'image initiale. Le processus forward nous permet d'effectuer cette opération, en commençant par une image claire et en progressant vers une image bruitée à l'horodatage t.

Algorithme de formation

Nous supposons que l'architecture du modèle utilisée pour faire des prédictions sera un U-Net. L'objectif de la phase de formation est le suivant : pour chaque image de l'ensemble de données, sélectionnez aléatoirement un horodatage dans la plage [0, T] et calculez le processus de diffusion vers l'avant. Cela produit une image claire et quelque peu bruyante, ainsi que le bruit réel utilisé. Ce modèle est ensuite utilisé pour prédire le bruit ajouté à l'image en utilisant notre compréhension du processus inverse. Avec le bruit réel et prévu, nous semblons être entrés dans un problème d’apprentissage automatique supervisé.

La question principale se pose : quelle fonction de perte devrions-nous utiliser pour entraîner notre modèle ? Puisque nous avons affaire à l'espace latent probabiliste, la divergence de Kullback-Leibler (KL) est un choix approprié.

La divergence KL mesure la différence entre deux distributions de probabilité, dans notre cas, la distribution prédite par le modèle et la distribution attendue. L'intégration de la divergence KL dans la fonction de perte guide non seulement le modèle pour produire des prédictions précises, mais garantit également que la représentation de l'espace latent est conforme à la structure de probabilité souhaitée.

La divergence KL peut être approchée comme la fonction de perte L2, de sorte que la fonction de perte suivante peut être obtenue :

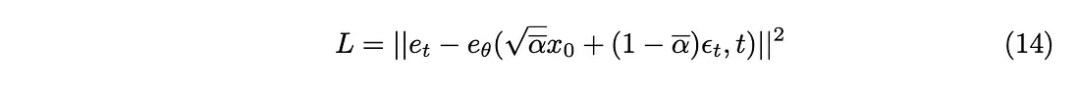
Enfin, nous obtenons l'algorithme d'entraînement proposé dans l'article.

Sampling

Le processus inverse a été expliqué, voici comment l'utiliser. En partant d’une image complètement aléatoire au temps T, et en utilisant le processus inverse T fois, on atteint finalement le temps 0. Cela forme le deuxième algorithme décrit dans cet article

Paramètres

Nous avons beaucoup de paramètres différents beta, beta_tildes, alpha, alpha_hat et ainsi de suite. Je ne sais toujours pas comment choisir ces paramètres. Mais le seul paramètre connu à ce stade est T, qui est fixé à 1 000.

Pour tous les paramètres répertoriés, leur sélection dépend de la version bêta. Dans un sens, Beta détermine la quantité de bruit que nous souhaitons ajouter à chaque étape. Par conséquent, pour garantir le succès de l’algorithme, une sélection bêta minutieuse est cruciale. Parce qu'il y a trop d'autres paramètres, veuillez vous référer au document.

Diverses méthodes d'échantillonnage ont été explorées au cours de la phase expérimentale de l'article original. Les images de la méthode d'échantillonnage linéaire d'origine recevaient soit un bruit insuffisant, soit devenaient trop bruyantes. Pour résoudre ce problème, une autre méthode plus courante est adoptée, à savoir l’échantillonnage cosinus. L'échantillonnage cosinus permet un ajout de bruit plus fluide et plus cohérent.

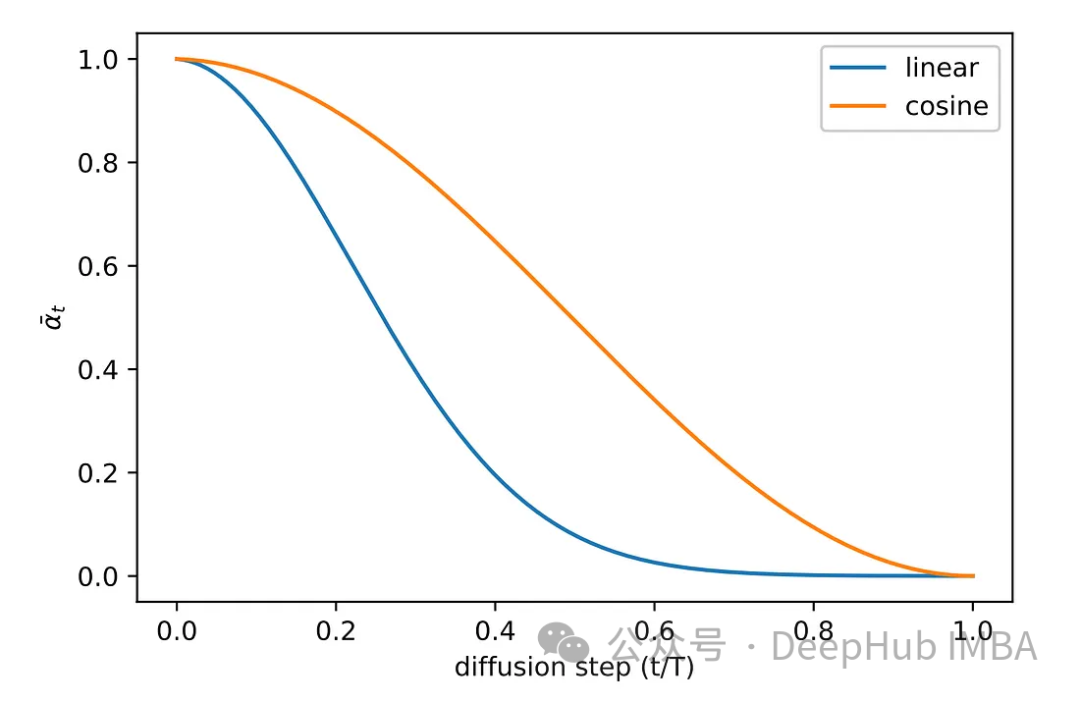
Implémentation du modèle Pytorch

Nous utiliserons l'architecture U-Net pour la prédiction du bruit La raison pour laquelle U-Net a été choisi est que U-Net est le meilleur pour le traitement d'images, la capture spatiale et caractéristique. cartes et fournissant une architecture d'entrée idéale pour la même taille de sortie.

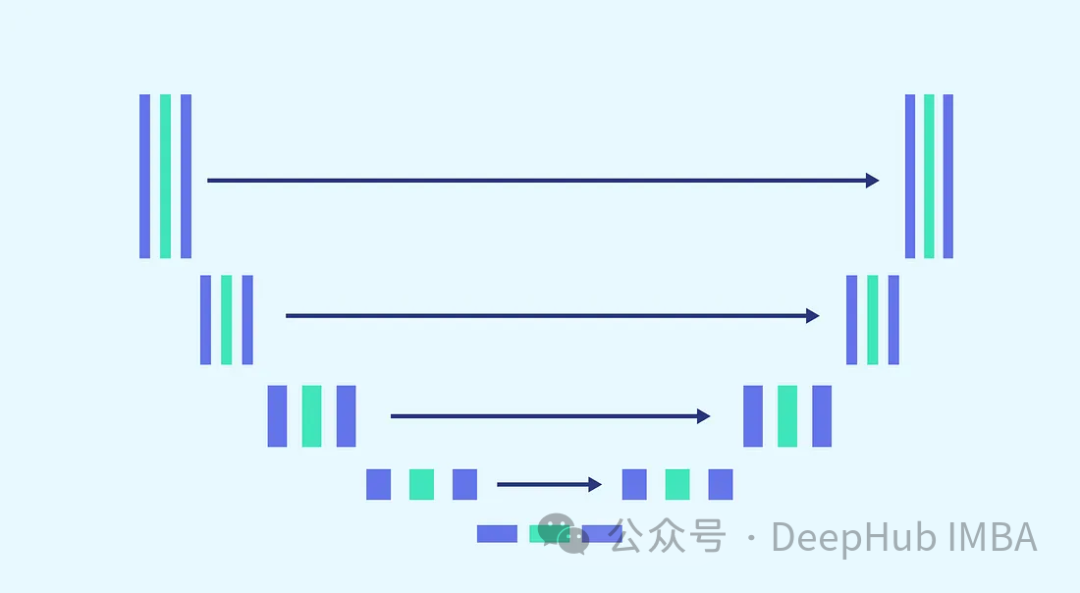
Compte tenu de la complexité de la tâche et de la nécessité d'utiliser le même modèle pour chaque étape (où le modèle doit être capable de débruiter les images entièrement bruitées et les images légèrement bruitées avec le même poids), régler le modèle est un incontournable. Indispensable. Cela inclut la fusion de blocs plus complexes et la prise en compte des horodatages utilisés via une étape d'intégration sinusoïdale. Le but de ces améliorations est de faire du modèle un expert dans les tâches de débruitage. Nous présenterons chaque bloc avant de procéder à la construction du modèle complet.

ConvNext Block

Afin de répondre au besoin d'augmenter la complexité du modèle, le bloc de convolution joue un rôle essentiel. Nous ne pouvons pas nous fier uniquement aux blocs de base du document u-net ici, nous les combinerons avec ConvNext.

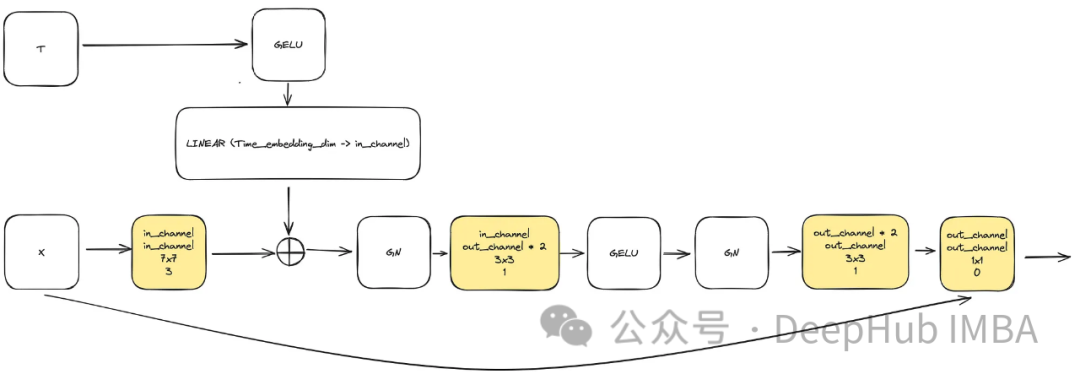
L'entrée se compose de "x" représentant l'image et d'une visualisation d'horodatage intégrée "t" de taille "time_embedding_dim". Tout au long du processus, les blocs jouent un rôle clé dans l'apprentissage des cartes spatiales et caractéristiques en raison de leur complexité et de leurs connexions résiduelles avec la couche d'entrée et la couche finale.

class ConvNextBlock(nn.Module):def __init__(self,in_channels,out_channels,mult=2,time_embedding_dim=None,norm=True,group=8,):super().__init__()self.mlp = (nn.Sequential(nn.GELU(), nn.Linear(time_embedding_dim, in_channels))if time_embedding_dimelse None) self.in_conv = nn.Conv2d(in_channels, in_channels, 7, padding=3, groups=in_channels) self.block = nn.Sequential(nn.GroupNorm(1, in_channels) if norm else nn.Identity(),nn.Conv2d(in_channels, out_channels * mult, 3, padding=1),nn.GELU(),nn.GroupNorm(1, out_channels * mult),nn.Conv2d(out_channels * mult, out_channels, 3, padding=1),) self.residual_conv = (nn.Conv2d(in_channels, out_channels, 1)if in_channels != out_channelselse nn.Identity()) def forward(self, x, time_embedding=None):h = self.in_conv(x)if self.mlp is not None and time_embedding is not None:assert self.mlp is not None, "MLP is None"h = h + rearrange(self.mlp(time_embedding), "b c -> b c 1 1")h = self.block(h)return h + self.residual_conv(x)

Incorporation d'horodatage sinusoïdal

L'un des blocs clés du modèle est le bloc d'intégration d'horodatage sinusoïdal, qui permet à l'encodage d'un horodatage donné de conserver des informations sur l'heure actuelle requise pour que le modèle décode, car le Le modèle sera utilisé pour tous les différents horodatages. Ceci est une implémentation très classique et elle est appliquée à divers endroits. Le module l'utilise pour créer une représentation temporelle basée sur un horodatage t donné. La sortie de ce perceptron multicouche (MLP) servira également d'entrée « t » à tous les blocs ConvNext modifiés.

Ici, "dim" est un hyperparamètre du modèle, indiquant le nombre de canaux requis pour le premier bloc. Il sert de base de calcul pour le nombre de canaux dans les blocs suivants.

class SinusoidalPosEmb(nn.Module):def __init__(self, dim, theta=10000):super().__init__()self.dim = dimself.theta = theta def forward(self, x):device = x.devicehalf_dim = self.dim // 2emb = math.log(self.theta) / (half_dim - 1)emb = torch.exp(torch.arange(half_dim, device=device) * -emb)emb = x[:, None] * emb[None, :]emb = torch.cat((emb.sin(), emb.cos()), dim=-1)return emb

Attention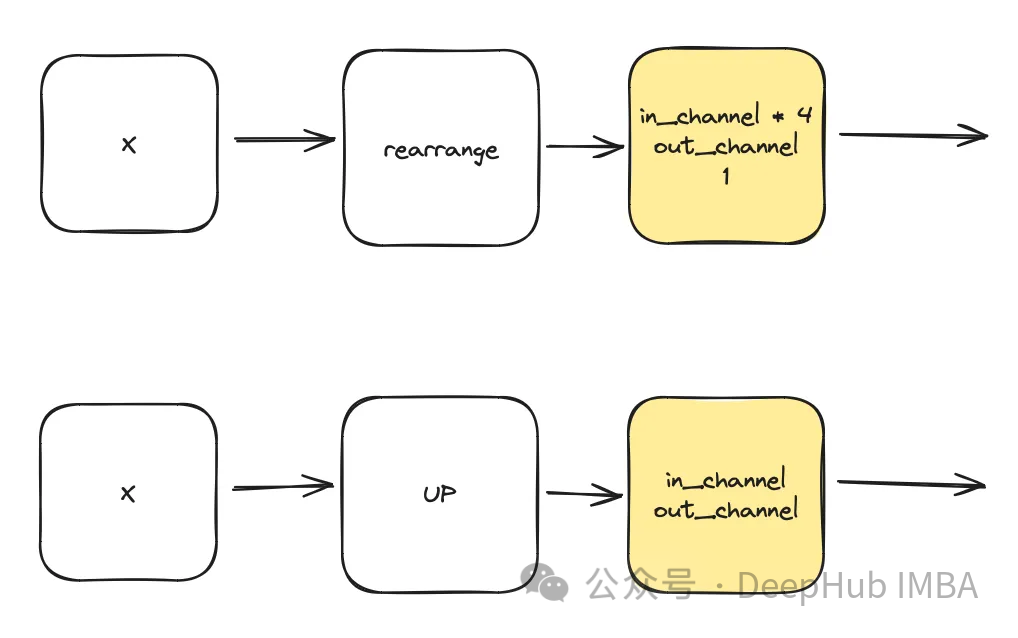

Il s'agit d'un composant facultatif utilisé dans unet. L’attention contribue à renforcer le rôle des connexions résiduelles dans l’apprentissage. Il accorde plus d'attention aux informations spatiales importantes obtenues du côté gauche d'Unet grâce au mécanisme d'attention calculé par les connexions résiduelles et à la carte des caractéristiques calculée par les espaces latents moyens et faibles. Cela vient du document ACC-UNet.

gate représente la sortie suréchantillonnée du bloc inférieur, tandis que x-residual représente la connexion résiduelle au niveau où l'attention est appliquée.

class BlockAttention(nn.Module):def __init__(self, gate_in_channel, residual_in_channel, scale_factor):super().__init__()self.gate_conv = nn.Conv2d(gate_in_channel, gate_in_channel, kernel_size=1, stride=1)self.residual_conv = nn.Conv2d(residual_in_channel, gate_in_channel, kernel_size=1, stride=1)self.in_conv = nn.Conv2d(gate_in_channel, 1, kernel_size=1, stride=1)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid() def forward(self, x: torch.Tensor, g: torch.Tensor) -> torch.Tensor:in_attention = self.relu(self.gate_conv(g) + self.residual_conv(x))in_attention = self.in_conv(in_attention)in_attention = self.sigmoid(in_attention)return in_attention * x

最后整合

将前面讨论的所有块(不包括注意力块)整合到一个Unet中。每个块都包含两个残差连接，而不是一个。这个修改是为了解决潜在的过度拟合问题。

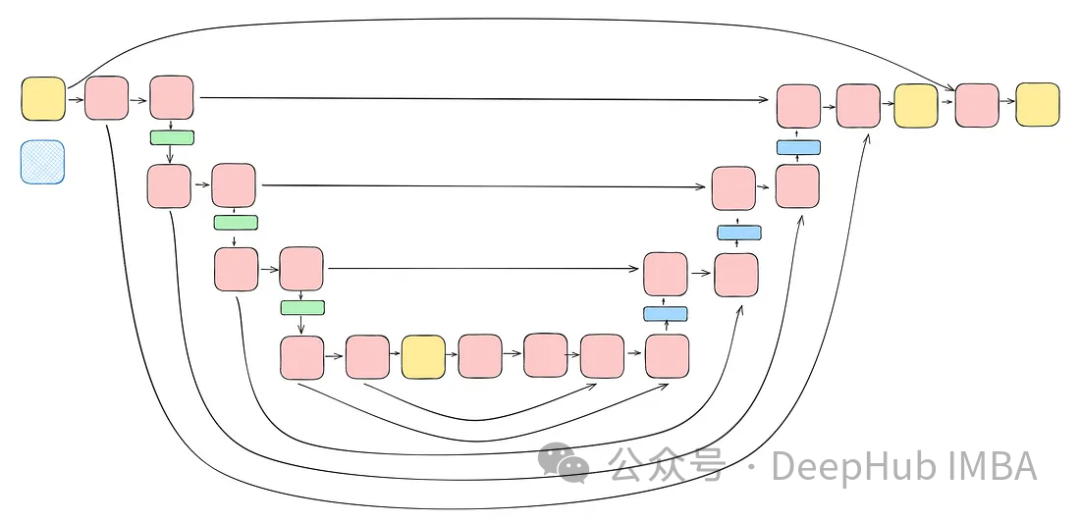
class TwoResUNet(nn.Module):def __init__(self,dim,init_dim=None,out_dim=None,dim_mults=(1, 2, 4, 8),channels=3,sinusoidal_pos_emb_theta=10000,convnext_block_groups=8,):super().__init__()self.channels = channelsinput_channels = channelsself.init_dim = default(init_dim, dim)self.init_conv = nn.Conv2d(input_channels, self.init_dim, 7, padding=3) dims = [self.init_dim, *map(lambda m: dim * m, dim_mults)]in_out = list(zip(dims[:-1], dims[1:])) sinu_pos_emb = SinusoidalPosEmb(dim, theta=sinusoidal_pos_emb_theta) time_dim = dim * 4 self.time_mlp = nn.Sequential(sinu_pos_emb,nn.Linear(dim, time_dim),nn.GELU(),nn.Linear(time_dim, time_dim),) self.downs = nn.ModuleList([])self.ups = nn.ModuleList([])num_resolutions = len(in_out) for ind, (dim_in, dim_out) in enumerate(in_out):is_last = ind >= (num_resolutions - 1) self.downs.append(nn.ModuleList([ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),DownSample(dim_in, dim_out)if not is_lastelse nn.Conv2d(dim_in, dim_out, 3, padding=1),])) mid_dim = dims[-1]self.mid_block1 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)self.mid_block2 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim) for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):is_last = ind == (len(in_out) - 1)is_first = ind == 0 self.ups.append(nn.ModuleList([ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),Upsample(dim_out, dim_in)if not is_lastelse nn.Conv2d(dim_out, dim_in, 3, padding=1)])) default_out_dim = channelsself.out_dim = default(out_dim, default_out_dim) self.final_res_block = ConvNextBlock(dim * 2, dim, time_embedding_dim=time_dim)self.final_conv = nn.Conv2d(dim, self.out_dim, 1) def forward(self, x, time):b, _, h, w = x.shapex = self.init_conv(x)r = x.clone() t = self.time_mlp(time) unet_stack = []for down1, down2, downsample in self.downs:x = down1(x, t)unet_stack.append(x)x = down2(x, t)unet_stack.append(x)x = downsample(x) x = self.mid_block1(x, t)x = self.mid_block2(x, t) for up1, up2, upsample in self.ups:x = torch.cat((x, unet_stack.pop()), dim=1)x = up1(x, t)x = torch.cat((x, unet_stack.pop()), dim=1)x = up2(x, t)x = upsample(x) x = torch.cat((x, r), dim=1)x = self.final_res_block(x, t) return self.final_conv(x)

扩散的代码实现

最后我们介绍一下扩散是如何实现的。由于我们已经介绍了用于正向、逆向和采样过程的所有数学理论，所里这里将重点介绍代码。

class DiffusionModel(nn.Module):SCHEDULER_MAPPING = {"linear": linear_beta_schedule,"cosine": cosine_beta_schedule,"sigmoid": sigmoid_beta_schedule,} def __init__(self,model: nn.Module,image_size: int,*,beta_scheduler: str = "linear",timesteps: int = 1000,schedule_fn_kwargs: dict | None = None,auto_normalize: bool = True,) -> None:super().__init__()self.model = model self.channels = self.model.channelsself.image_size = image_size self.beta_scheduler_fn = self.SCHEDULER_MAPPING.get(beta_scheduler)if self.beta_scheduler_fn is None:raise ValueError(f"unknown beta schedule {beta_scheduler}") if schedule_fn_kwargs is None:schedule_fn_kwargs = {} betas = self.beta_scheduler_fn(timesteps, **schedule_fn_kwargs)alphas = 1.0 - betasalphas_cumprod = torch.cumprod(alphas, dim=0)alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)posterior_variance = (betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)) register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32)) register_buffer("betas", betas)register_buffer("alphas_cumprod", alphas_cumprod)register_buffer("alphas_cumprod_prev", alphas_cumprod_prev)register_buffer("sqrt_recip_alphas", torch.sqrt(1.0 / alphas))register_buffer("sqrt_alphas_cumprod", torch.sqrt(alphas_cumprod))register_buffer("sqrt_one_minus_alphas_cumprod", torch.sqrt(1.0 - alphas_cumprod))register_buffer("posterior_variance", posterior_variance) timesteps, *_ = betas.shapeself.num_timesteps = int(timesteps) self.sampling_timesteps = timesteps self.normalize = normalize_to_neg_one_to_one if auto_normalize else identityself.unnormalize = unnormalize_to_zero_to_one if auto_normalize else identity @torch.inference_mode()def p_sample(self, x: torch.Tensor, timestamp: int) -> torch.Tensor:b, *_, device = *x.shape, x.devicebatched_timestamps = torch.full((b,), timestamp, device=device, dtype=torch.long) preds = self.model(x, batched_timestamps) betas_t = extract(self.betas, batched_timestamps, x.shape)sqrt_recip_alphas_t = extract(self.sqrt_recip_alphas, batched_timestamps, x.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, batched_timestamps, x.shape) predicted_mean = sqrt_recip_alphas_t * (x - betas_t * preds / sqrt_one_minus_alphas_cumprod_t) if timestamp == 0:return predicted_meanelse:posterior_variance = extract(self.posterior_variance, batched_timestamps, x.shape)noise = torch.randn_like(x)return predicted_mean + torch.sqrt(posterior_variance) * noise @torch.inference_mode()def p_sample_loop(self, shape: tuple, return_all_timesteps: bool = False) -> torch.Tensor:batch, device = shape[0], "mps" img = torch.randn(shape, device=device)# This cause me a RunTimeError on MPS device due to MPS back out of memory# No ideas how to resolve it at this point # imgs = [img] for t in tqdm(reversed(range(0, self.num_timesteps)), total=self.num_timesteps):img = self.p_sample(img, t)# imgs.append(img) ret = img # if not return_all_timesteps else torch.stack(imgs, dim=1) ret = self.unnormalize(ret)return ret def sample(self, batch_size: int = 16, return_all_timesteps: bool = False) -> torch.Tensor:shape = (batch_size, self.channels, self.image_size, self.image_size)return self.p_sample_loop(shape, return_all_timesteps=return_all_timesteps) def q_sample(self, x_start: torch.Tensor, t: int, noise: torch.Tensor = None) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start) sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise def p_loss(self,x_start: torch.Tensor,t: int,noise: torch.Tensor = None,loss_type: str = "l2",) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start)x_noised = self.q_sample(x_start, t, noise=noise)predicted_noise = self.model(x_noised, t) if loss_type == "l2":loss = F.mse_loss(noise, predicted_noise)elif loss_type == "l1":loss = F.l1_loss(noise, predicted_noise)else:raise ValueError(f"unknown loss type {loss_type}")return loss def forward(self, x: torch.Tensor) -> torch.Tensor:b, c, h, w, device, img_size = *x.shape, x.device, self.image_sizeassert h == w == img_size, f"image size must be {img_size}" timestamp = torch.randint(0, self.num_timesteps, (1,)).long().to(device)x = self.normalize(x)return self.p_loss(x, timestamp)

扩散过程是训练部分的模型。它打开了一个采样接口，允许我们使用已经训练好的模型生成样本。

训练的要点总结

对于训练部分，我们设置了37,000步的训练，每步16个批次。由于GPU内存分配限制，图像大小被限制为128x128。使用指数移动平均(EMA)模型权重每1000步生成样本以平滑采样，并保存模型版本。

在最初的1000步训练中，模型开始捕捉一些特征，但仍然错过了某些区域。在10000步左右，这个模型开始产生有希望的结果，进步变得更加明显。在3万步的最后，结果的质量显著提高，但仍然存在黑色图像。这只是因为模型没有足够的样本种类，真实图像的数据分布并没有完全映射到高斯分布。

有了最终的模型权重，我们可以生成一些图片。尽管由于128x128的尺寸限制，图像质量受到限制，但该模型的表现还是不错的。

注：本文使用的数据集是森林地形的卫星图片，具体获取方式请参考源代码中的ETL部分。

总结

我们已经完整的介绍了有关扩散模型的必要知识，并且使用Pytorch进行了完整的实现，本文的代码：

https://github.com/Camaltra/this-is-not-real-aerial-imagery/

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!