Exemple de code de prédiction de lien utilisant Pytorch Geographic

PyTorch Geographic (PyG) est le principal outil permettant de créer des modèles de réseaux neuronaux graphiques et d'expérimenter diverses convolutions graphiques. Dans cet article, nous le présenterons à travers la prédiction de liens.

La prédiction de liens répond à la question : quels deux nœuds doivent être liés l'un à l'autre ? Nous préparerons les données pour la modélisation en effectuant une "transformation split". Préparez un chargeur de données graphiques dédié pour le traitement par lots. Créez un modèle dans Torch Geographic, entraînez-le à l'aide de PyTorch Lightning et vérifiez les performances du modèle.

Préparation de la bibliothèque

• Torch Cela n'a pas besoin d'être présenté davantage
• Torch est la bibliothèque principale du réseau neuronal de graphes géométriques et l'objet de cet article
• PyTorch Lightning est utilisé pour entraîner, régler et vérifier le modèle. Cela simplifie le fonctionnement de la formation
• Sklearn Metrics et Torchmetrics sont utilisés pour vérifier les performances du modèle.
• PyTorch Geographic a quelques dépendances spécifiques, si vous rencontrez des problèmes pour l'installer, veuillez vous référer à sa documentation officielle.

Préparation des données

Nous utiliserons l'ensemble de données de citation Cora ML. L’ensemble de données est accessible via Torch Geographic.

 data = tg.datasets.CitationFull(root="data", name="Cora_ML")

Par défaut, l'ensemble de données Torch Geographic peut renvoyer plusieurs graphiques. Voyons à quoi ressemble un graphique unique

data[0] > Data(x=[2995, 2879], edge_index=[2, 16316], y=[2995])

où X est la caractéristique du nœud. edge_index est une matrice 2 x (n bords) (première dimension = 2, interprétée comme : ligne 0 - nœud source/"expéditeur", ligne 1 - nœud cible/"récepteur").

Link Splitting

Nous commencerons par diviser les liens dans l'ensemble de données. Utilisez 20 % des liens graphiques comme ensemble de validation et 10 % comme ensemble de test. Les échantillons négatifs ne seront pas ajoutés à l'ensemble de données d'entraînement ici, car ces liens négatifs seront créés à la volée par le chargeur de données par lots.

En général, l'échantillonnage négatif crée des "faux" échantillons (dans notre cas des liens entre nœuds), le modèle apprend donc à distinguer les liens réels des faux. L'échantillonnage négatif est basé sur la théorie et les mathématiques de l'échantillonnage et possède de belles propriétés statistiques.

Tout d’abord : créons un objet de partage de lien.

 link_splitter = tg.transforms.RandomLinkSplit(num_val=0.2, num_test=0.1, add_negative_train_samples=False,disjoint_train_ratio=0.8)

disjoint_train_ratio ajuste le nombre d'arêtes qui seront utilisées comme informations d'entraînement dans la phase de "supervision". Les bords restants seront utilisés pour la transmission des messages (la phase de transfert d'informations dans le réseau).

Il existe au moins deux méthodes de segmentation des bords dans les réseaux de neurones graphiques : la segmentation inductive et la segmentation conductrice. La méthode de transformation suppose que GNN doit apprendre des modèles structurels à partir de structures graphiques. Dans un cadre inductif, les étiquettes de nœuds/bords peuvent être utilisées pour l’apprentissage. Il y a deux articles à la fin de cet article qui discutent de ces concepts en détail et fournissent une formalisation supplémentaire : ([1], [3]).

 train_g, val_g, test_g = link_splitter(data[0])  > Data(x=[2995, 2879], edge_index=[2, 2285], y=[2995], edge_label=[9137], edge_label_index=[2, 9137])

Après cette opération, nous avons de nouveaux attributs :

edge_label : décrit si le bord est vrai/faux. C'est ce que nous voulons prédire.

edge_label_index est une matrice 2 x NUM EDGES utilisée pour stocker les liens de nœuds.

Regardons la répartition des échantillons

th.unique(train_g.edge_label, return_counts=True) > (tensor([1.]), tensor([9137]))  th.unique(val_g.edge_label, return_counts=True) > (tensor([0., 1.]), tensor([3263, 3263]))  th.unique(val_g.edge_label, return_counts=True) > (tensor([0., 1.]), tensor([3263, 3263]))

Pour les données d'entraînement il n'y a pas d'arêtes négatives (nous les créerons pendant l'entraînement), pour l'ensemble val/test - il y a déjà quelques "faux" liens dans un 50 : rapport 50.

Modèle

Maintenant, nous pouvons construire un modèle en utilisant GNN en construisant une

class GNN(nn.Module):

def __init__(self, dim_in: int, conv_sizes: Tuple[int, ...], act_f: nn.Module = th.relu, dropout: float = 0.1,*args, **kwargs):super().__init__()self.dim_in = dim_inself.dim_out = conv_sizes[-1]self.dropout = dropoutself.act_f = act_flast_in = dim_inlayers = [] # Here we build subsequent graph convolutions.for conv_sz in conv_sizes:# Single graph convolution layerconv = tgnn.SAGEConv(in_channels=last_in, out_channels=conv_sz, *args, **kwargs)last_in = conv_szlayers.append(conv)self.layers = nn.ModuleList(layers) def forward(self, x: th.Tensor, edge_index: th.Tensor) -> th.Tensor:h = x# For every graph convolution in the network...for conv in self.layers:# ... perform node embedding via message passingh = conv(h, edge_index)h = self.act_f(h)if self.dropout:h = nn.functional.dropout(h, p=self.dropout, training=self.training)return h

La partie remarquable de ce modèle est un ensemble de convolutions graphiques - dans notre cas, c'est SAGEConv. La définition formelle de la convolution SAGE est la suivante :

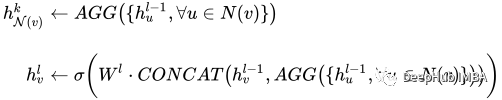å¾ç

v est le nœud actuel, les N(v) voisins du nœud v. Pour en savoir plus sur ce type de convolution, consultez l'article original de GraphSAGE[1]

Vérifions si le modèle peut faire des prédictions en utilisant les données préparées. L'entrée du modèle PyG ici est la matrice des caractéristiques des nœuds X et le lien définissant edge_index.

gnn = GNN(train_g.x.size()[1], conv_sizes=[512, 256, 128]) with th.no_grad():out = gnn(train_g.x, train_g.edge_index)  out   > tensor([[0.0000, 0.0000, 0.0051, ..., 0.0997, 0.0000, 0.0000],[0.0107, 0.0000, 0.0576, ..., 0.0651, 0.0000, 0.0000],[0.0000, 0.0000, 0.0102, ..., 0.0973, 0.0000, 0.0000],...,[0.0000, 0.0000, 0.0549, ..., 0.0671, 0.0000, 0.0000],[0.0000, 0.0000, 0.0166, ..., 0.0000, 0.0000, 0.0000],[0.0000, 0.0000, 0.0034, ..., 0.1111, 0.0000, 0.0000]])

La sortie de notre modèle est une matrice d'intégration de nœuds avec des dimensions : N nœuds x taille d'intégration.

PyTorch Lightning

PyTorch Lightning est principalement utilisé pour la formation, mais ici nous ajoutons une couche linéaire après la sortie de GNN comme tête de sortie pour prédire s'il faut établir une liaison.

class LinkPredModel(pl.LightningModule) :

def __init__(self,dim_in: int,conv_sizes: Tuple[int, ...], act_f: nn.Module = th.relu, dropout: float = 0.1,lr: float = 0.01,*args, **kwargs):super().__init__() # Our inner GNN modelself.gnn = GNN(dim_in, conv_sizes=conv_sizes, act_f=act_f, dropout=dropout) # Final prediction model on links.self.lin_pred = nn.Linear(self.gnn.dim_out, 1)self.lr = lr def forward(self, x: th.Tensor, edge_index: th.Tensor) -> th.Tensor:# Step 1: make node embeddings using GNN.h = self.gnn(x, edge_index) # Take source nodes embeddings- sendersh_src = h[edge_index[0, :]]# Take target node embeddings - receiversh_dst = h[edge_index[1, :]] # Calculate the product between themsrc_dst_mult = h_src * h_dst# Apply non-linearityout = self.lin_pred(src_dst_mult)return out def _step(self, batch: th.Tensor, phase: str='train') -> th.Tensor:yhat_edge = self(batch.x, batch.edge_label_index).squeeze()y = batch.edge_labelloss = nn.functional.binary_cross_entropy_with_logits(input=yhat_edge, target=y)f1 = tm.functional.f1_score(preds=yhat_edge, target=y, task='binary')prec = tm.functional.precision(preds=yhat_edge, target=y, task='binary')recall = tm.functional.recall(preds=yhat_edge, target=y, task='binary') # Watch for logging here - we need to provide batch_size, as (at the time of this implementation)# PL cannot understand the batch size.self.log(f"{phase}_f1", f1, batch_size=batch.edge_label_index.shape[1])self.log(f"{phase}_loss", loss, batch_size=batch.edge_label_index.shape[1])self.log(f"{phase}_precision", prec, batch_size=batch.edge_label_index.shape[1])self.log(f"{phase}_recall", recall, batch_size=batch.edge_label_index.shape[1])return loss def training_step(self, batch, batch_idx):return self._step(batch) def validation_step(self, batch, batch_idx):return self._step(batch, "val") def test_step(self, batch, batch_idx):return self._step(batch, "test") def predict_step(self, batch):x, edge_index = batchreturn self(x, edge_index) def configure_optimizers(self):return th.optim.Adam(self.parameters(), lr=self.lr)

Le rôle de PyTorch Lightning est de nous aider à simplifier les étapes de formation Il nous suffit de configurer certaines fonctions. Nous pouvons utiliser la commande suivante pour tester si le modèle est disponible

 model = LinkPredModel(val_g.x.size()[1], conv_sizes=[512, 256, 128]) with th.no_grad():out = model.predict_step((val_g.x, val_g.edge_label_index))

.

Formation

Pour l'étape de formation, le chargeur de données nécessite un traitement spécial.

Les données graphiques nécessitent un traitement spécial, notamment la prédiction de liens. PyG dispose de classes de chargeur de données spécialisées qui sont chargées de générer correctement les lots. Nous utiliserons : tg.loader.LinkNeighborLoader, qui accepte l'entrée suivante :

Données à charger en masse (image). num_neighbors Nombre maximum de voisins à charger par nœud pendant un "saut". Une liste précisant le nombre de voisins 1 - 2 - 3 -…-K. Particulièrement utile pour les très grands graphiques.

edge_label_index dont l'attribut indique déjà des liens vrais/faux.

neg_sampling_ratio - le rapport entre les échantillons négatifs et les échantillons réels.

 train_loader = tg.loader.LinkNeighborLoader(train_g,num_neighbors=[-1, 10, 5],batch_size=128,edge_label_index=train_g.edge_label_index, # "on the fly" negative sampling creation for batchneg_sampling_ratio=0.5 )  val_loader = tg.loader.LinkNeighborLoader(val_g,num_neighbors=[-1, 10, 5],batch_size=128,edge_label_index=val_g.edge_label_index,edge_label=val_g.edge_label, # negative samples for val set are done already as ground-truthneg_sampling_ratio=0.0 )  test_loader = tg.loader.LinkNeighborLoader(test_g,num_neighbors=[-1, 10, 5],batch_size=128,edge_label_index=test_g.edge_label_index,edge_label=test_g.edge_label, # negative samples for test set are done already as ground-truthneg_sampling_ratio=0.0 )

Ce qui suit est le modèle de formation

model = LinkPredModel(val_g.x.size()[1], conv_sizes=[512, 256, 128]) trainer = pl.Trainer(max_epochs=20, log_every_n_steps=5)  # Validate before training - we will see results of untrained model. trainer.validate(model, val_loader)  # Train the model trainer.fit(model=model, train_dataloaders=train_loader, val_dataloaders=val_loader)

Testez la vérification des données, consultez le rapport de classification et la courbe ROC.

with th.no_grad():yhat_test_proba = th.sigmoid(model(test_g.x, test_g.edge_label_index)).squeeze()yhat_test_cls = yhat_test_proba >= 0.5  print(classification_report(y_true=test_g.edge_label, y_pred=yhat_test_cls))

Les résultats semblent plutôt bons :

precision recall f1-score support0.0 0.68 0.70 0.69 16311.0 0.69 0.66 0.68 1631accuracy 0.68 3262macro avg 0.68 0.68 0.68 3262

ROC曲线也不错

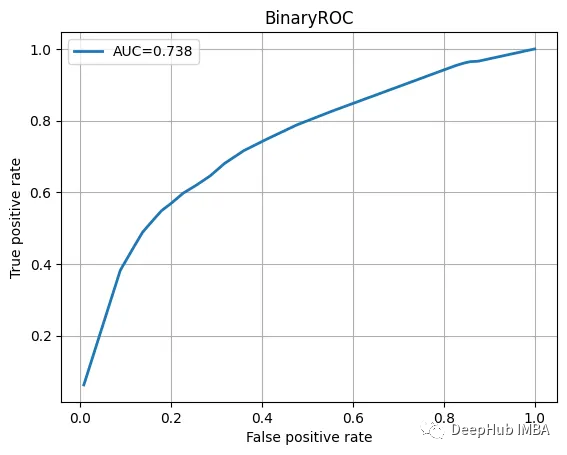
我们训练的模型并不特别复杂，也没有经过精心调整，但它完成了工作。当然这只是一个为了演示使用的小型数据集。

总结

图神经网络尽管看起来很复杂，但是PyTorch Geometric为我们提供了一个很好的解决方案。我们可以直接使用其中内置的模型实现，这方便了我们使用和简化了入门的门槛。

本文代码：https://github.com/maddataanalyst/blogposts_code/blob/main/graph_nns_series/pyg_pyl_perfect_match/pytorch-geometric-lightning-perfect-match.ipynb

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!