1 jeton met fin au problème du codage numérique LLM ! Neuf grandes institutions ont publié conjointement xVal : les chiffres qui ne sont pas inclus dans l'ensemble de formation peuvent également être prédits !

Bien que les performances des grands modèles de langage (LLM) soient très puissantes dans les tâches d'analyse et de génération de texte, face à des problèmes impliquant des nombres, tels que la multiplication à plusieurs chiffres, en raison de l'absence d'un mécanisme unifié et complet de segmentation des mots numériques au sein le modèle, il y aura des problèmes. En conséquence, LLM ne peut pas comprendre la sémantique des nombres et invente des réponses aléatoires.

À l'heure actuelle, l'un des obstacles pour lesquels le LLM n'a pas été largement utilisé dans l'analyse des données dans le domaine scientifique est le problème de l'encodage numérique.

Récemment, neuf instituts de recherche, dont le Flatiron Institute, le Lawrence Berkeley National Laboratory, l'Université de Cambridge, l'Université de New York et l'Université de Princeton, ont publié conjointement un nouveau système de codage numérique xVal, qui ne nécessite qu'un seul jeton pour coder tous les nombres.

Lien papier : https://arxiv.org/pdf/2310.02989.pdf

xVal représente la vraie valeur cible en mettant à l'échelle numérique le vecteur d'intégration du jeton dédié ([NUM]), et Ensuite, combinée à la méthode de raisonnement numérique modifiée, la stratégie xVal rend le modèle continu de bout en bout lors du mappage entre les numéros de chaîne d'entrée et les numéros de sortie, ce qui le rend plus adapté aux applications dans le domaine scientifique.

Les résultats de l'évaluation sur des ensembles de données synthétiques et réels montrent que xVal non seulement fonctionne mieux et enregistre plus de jetons que les schémas de codage numérique existants, mais présente également de meilleures propriétés de généralisation d'interpolation.

Nouvelle avancée dans le codage numérique

Le schéma standard de segmentation des mots LLM ne fait pas de distinction entre les nombres et le texte, il est donc impossible de quantifier les valeurs.

Des travaux antérieurs ont été réalisés pour mapper tous les nombres sur un ensemble limité de chiffres prototypes sous forme de notation scientifique, en utilisant 10 comme base, ou pour calculer la distance cosinus entre les incorporations de nombres pour refléter le nombre lui-même. a été utilisé avec succès pour résoudre des problèmes d’algèbre linéaire tels que la multiplication matricielle.

Cependant, pour les problèmes continus ou fluides dans le domaine scientifique, les modèles de langage ne peuvent toujours pas bien gérer les problèmes d'interpolation et de généralisation hors distribution, car après avoir codé les nombres en texte, LLM est toujours de nature discrète dans l'encodage et le décodage. étapes , il est difficile d'apprendre des fonctions continues approximatives. L'idée de

xVal est d'encoder de manière multiplicative la taille numérique et de l'orienter dans une direction apprenable dans l'espace d'intégration, ce qui change considérablement la façon dont les nombres sont traités et interprétés dans l'architecture Transformer.

xVal utilise un seul jeton pour l'encodage numérique, ce qui présente les avantages de l'efficacité des jetons et d'une empreinte de vocabulaire minimale.

Combinée au paradigme de raisonnement numérique modifié, la valeur du modèle Transformer est continue (lisse) lors du mappage entre les nombres d'entrée et les nombres de chaînes de sortie. Lorsque la fonction approximative est continue ou lisse, elle peut apporter plus de bons biais inductifs.

xVal : codage continu des nombres

xVal n'utilise pas différents jetons pour différents nombres, mais intègre directement les valeurs selon des directions d'apprentissage spécifiques dans l'espace d'intégration.

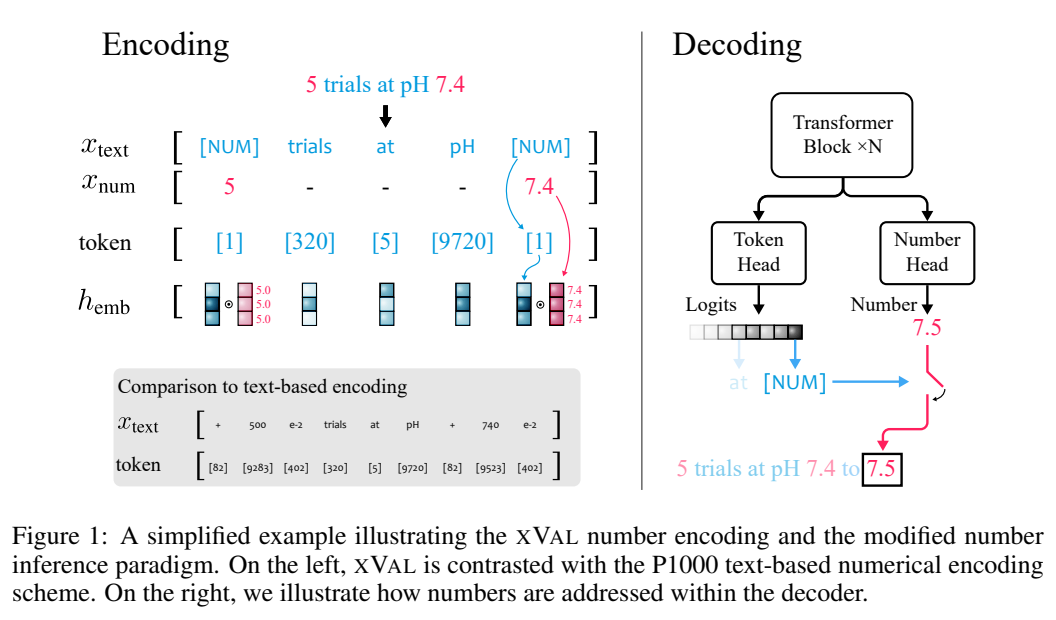
En supposant que la chaîne d'entrée contient à la fois des nombres et du texte, le système analysera d'abord l'entrée, extraira toutes les valeurs, puis construira une nouvelle chaîne dans laquelle les nombres sont remplacés par [NUM bit]. symbole, puis multipliez le vecteur d'incorporation de [NUM] par sa valeur correspondante.

L'ensemble du processus d'encodage peut être utilisé pour la modélisation du langage de masque (MLM) et la génération autorégressive (AR).

Normalisation implicite via une norme de couche basée sur la normalisation de couche

Dans l'implémentation spécifique, l'intégration multiplicative de xVal dans le premier bloc Transformer doit être ajoutée après que le vecteur de codage de position supérieure et la norme de couche normalisent l'intégration de chaque jeton en fonction de l'échantillon d'entrée.

Lorsque l'intégration de position n'est pas colinéaire avec l'intégration étiquetée [NUM], la valeur scalaire peut être transmise via une fonction de redimensionnement non linéaire.

Supposons que u est l'intégration de [NUM], p est l'intégration de position et x est la valeur scalaire codée, u · p = 0, où ∥u∥ =∥p. ∥ = 1, tu peux Got

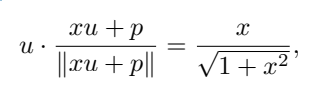
C'est-à-dire que la valeur de x est codée pour être dans la même direction que u, et cette propriété peut toujours être conservée après l'entraînement.

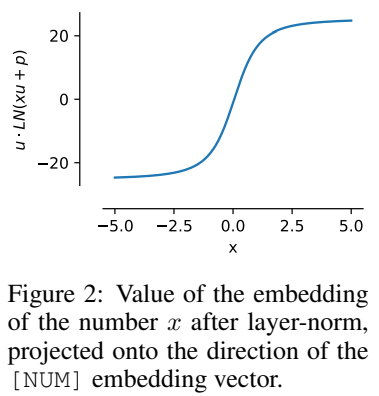
Cette caractéristique de normalisation signifie que la plage dynamique de xVal est plus petite que celle des autres schémas de codage basés sur du texte, qui est définie sur [-5, 5] dans l'expérience en tant qu'étapes de traitement de pré-entraînement.

Raisonnement numérique

xVal définit une intégration continue dans la valeur d'entrée, mais si une tâche multi-classification est utilisée comme sortie et que l'algorithme d'entraînement prend en compte le mappage de la valeur d'entrée à la valeur de sortie, le modèle dans son ensemble, ce n'est pas continu de bout en bout et les nombres doivent être traités séparément au niveau de la couche de sortie.

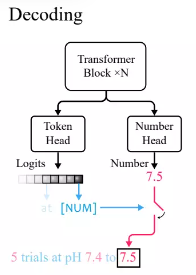
Selon la pratique standard du modèle de langage Transformer, les chercheurs ont défini une tête de jeton pour générer la distribution de probabilité des jetons de vocabulaire.

Parce que xVal utilise [NUM] pour remplacer les nombres, la tête ne contient aucune information sur la valeur numérique, donc une nouvelle tête numérique avec une sortie scalaire doit être introduite et entraînée via une perte d'erreur quadratique moyenne (MSE) pour Restaure la valeur numérique spécifique associée à [NUM].

Après avoir donné l'entrée, observez d'abord la sortie de la tête du jeton. Si le jeton généré est [NUM], regardez la tête numérique pour remplir la valeur du jeton.

Dans les expériences, comme le modèle Transformer est continu de bout en bout lors de la déduction de valeurs, il fonctionne mieux lors de l'interpolation vers des valeurs invisibles.

Partie expérimentale

Comparaison avec d'autres méthodes d'encodage numérique

Les chercheurs ont comparé les performances de XVAL avec quatre autres encodages numériques, qui nécessitent tous que les nombres soient traités dans la première forme ±ddd E±d, puis appelez un ou plusieurs jetons selon le format pour déterminer le codage.

Différentes méthodes présentent de grandes différences dans le nombre de jetons et le vocabulaire requis pour coder chaque nombre, mais dans l'ensemble, xVal a l'efficacité de codage la plus élevée et la plus petite taille de vocabulaire.

Les chercheurs ont également évalué xVal sur trois ensembles de données, notamment des données d'opérations arithmétiques synthétiques, des données de température globale et des données de simulation d'orbite planétaire.

Apprendre l'arithmétique

Même pour les plus grands LLM, la "multiplication à plusieurs chiffres" reste une tâche extrêmement difficile. Par exemple, GPT-4 n'atteint qu'une précision de 59 %, la précision sur quatre. -Les problèmes de multiplication à chiffres et à cinq chiffres ne sont que de 4% et 0%

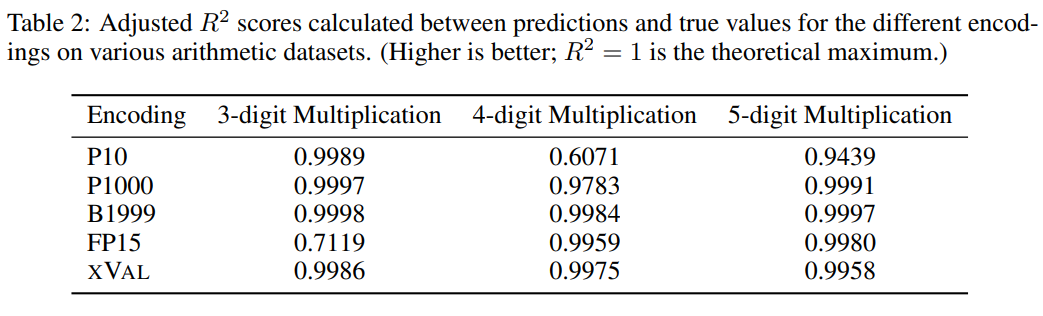
D'après les expériences comparatives, d'autres encodages numériques peuvent généralement également très bien fonctionner. Cela résout bien les problèmes de multiplication à plusieurs chiffres, mais les résultats de prédiction. de xVal sont plus stables que P10 et FP15 et ne produiront pas de valeurs de prédiction anormales.

Afin d'augmenter la difficulté de la tâche, les chercheurs ont utilisé des arbres binaires aléatoires pour construire un ensemble de données en utilisant des opérateurs binaires d'addition, de soustraction et de multiplication pour combiner un nombre fixe d'opérandes (2, 3 ou 4), en où chaque échantillon est une expression arithmétique, par exemple ((1,32 * 32,1) + (1,42-8,20)) = 35,592

Ensuite, les échantillons sont traités selon les exigences de traitement de chaque schéma de codage numérique, et l'objectif de la tâche est pour calculer le côté gauche de l'équation L'expression de , c'est-à-dire le côté droit de l'équation est le masque.

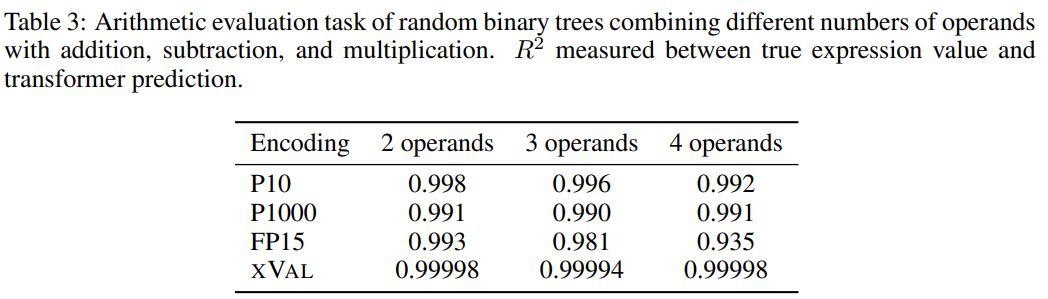
À en juger par les résultats, xVal s'est très bien comporté dans cette tâche, mais les expériences arithmétiques seules ne suffisent pas pour évaluer pleinement les capacités mathématiques du modèle de langage, car les échantillons dans les opérations arithmétiques sont généralement des séquences courtes et la variété de données sous-jacente est faible. -dimensionnelles, ces problèmes ne surmontent pas le goulot d'étranglement informatique des LLM et les applications dans le monde réel sont plus complexes.

Prévision de la température

Les chercheurs ont utilisé un sous-ensemble de l'ensemble de données climatiques mondiales ERA5 pour l'évaluation, par souci de simplicité, seules les données de température de surface (T2m dans ERA5) ont été ciblées dans l'expérience, et Ensuite, les échantillons ont été divisés, chaque échantillon comprenant 2 à 4 jours de données sur la température de surface (normalisées pour avoir une variance unitaire) et la latitude et la longitude provenant de 60 à 90 stations de déclaration sélectionnées au hasard.

Encodez le sinus de la latitude et le sinus et le cosinus de la longitude de la coordonnée, préservant ainsi la périodicité des données, puis utilisez la même opération pour encoder la position dans les périodes de 24 heures et 365 jours .

Les coordonnées (coords), le point de départ (start) et les données (data) correspondent aux coordonnées de la station de reporting, à l'heure du premier échantillon et aux données de température normalisées, puis utilisez la méthode MLM pour vous entraîner le modèle de langage.

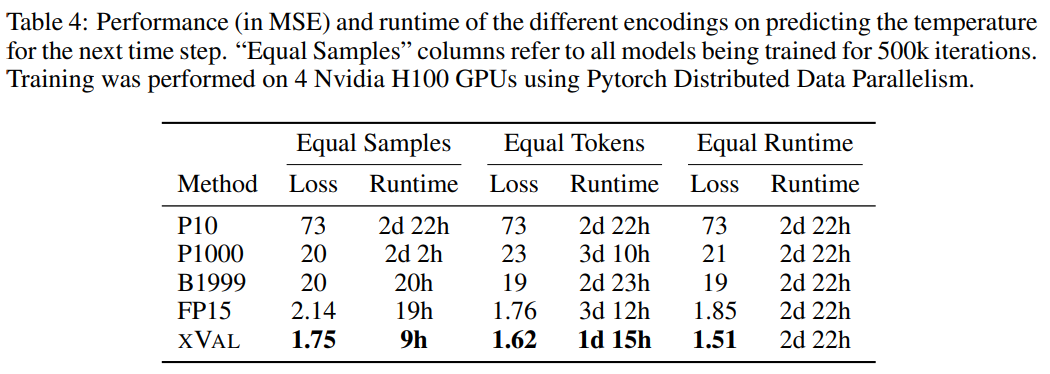
D'après les résultats, xVal a les meilleures performances, et le temps de calcul est également considérablement réduit.

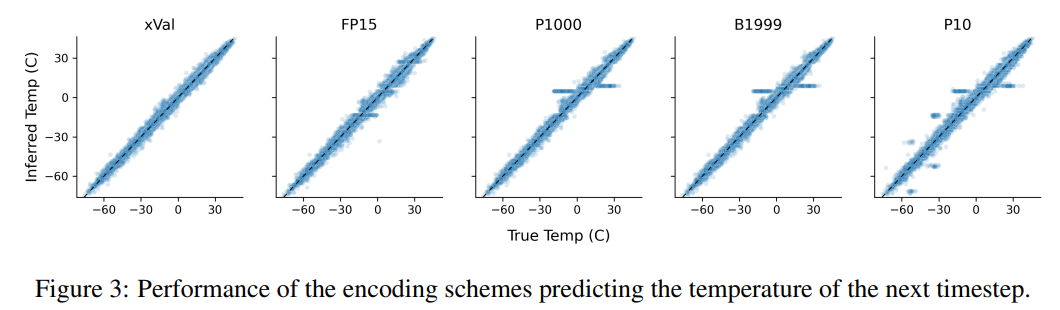
Cette tâche illustre également les lacunes des schémas de codage basés sur du texte, le modèle peut exploiter de fausses corrélations dans les données, c'est-à-dire que P10, P1000 et B1999 ont tendance à prédire une température normalisée de ±0,1, principalement parce que ce nombre apparaît le plus fréquemment dans l’ensemble de données.

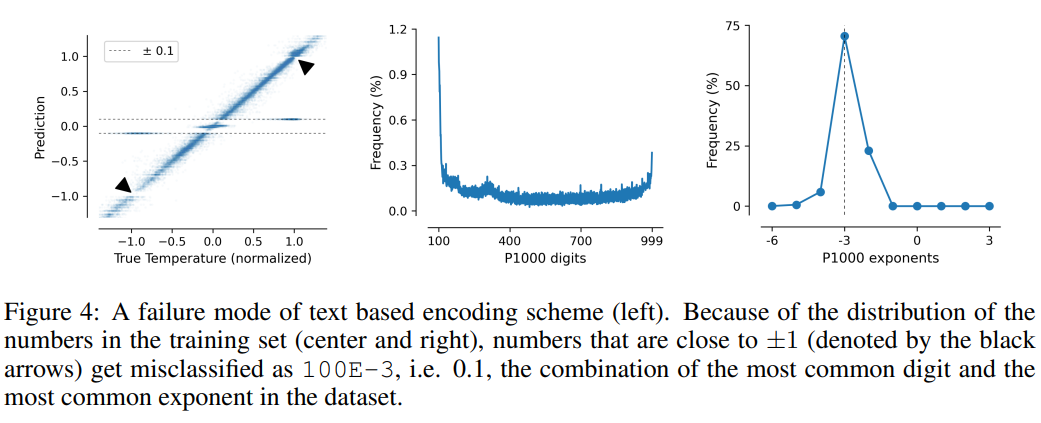
Pour les schémas P1000 et P10, la sortie d'encodage des deux schémas est respectivement d'environ 8 000 et 5 000 jetons (par rapport à la moyenne de FP15 et xVal d'environ 1 800 jetons), de mauvaises performances du modèle probablement dues aux problèmes de modélisation longue distance.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!