Terence Tao aborde un autre problème de géométrie vieux de 60 ans ! Une nouvelle avancée a été réalisée dans le problème du pavage périodique

Tao Zhexuan a fait une nouvelle percée dans l'étude du problème du carrelage périodique

Le 18 septembre, Tao Zhexuan et Rachel Greenfeld ont mis en ligne l'article préimprimé "Indécidabilité des monotilings translationnels" sur arXiv.

Adresse papier : https://arxiv.org/abs/2309.09504

La conclusion principale de cet article est que si la dimension de la grille est illimitée, alors déterminez la subdivision finie de la grille La question de savoir si un ensemble peut carreler un sous-ensemble périodique de la grille est indécidable

Vous savez, ce problème est décidable en dimension 1 et en dimension 2.

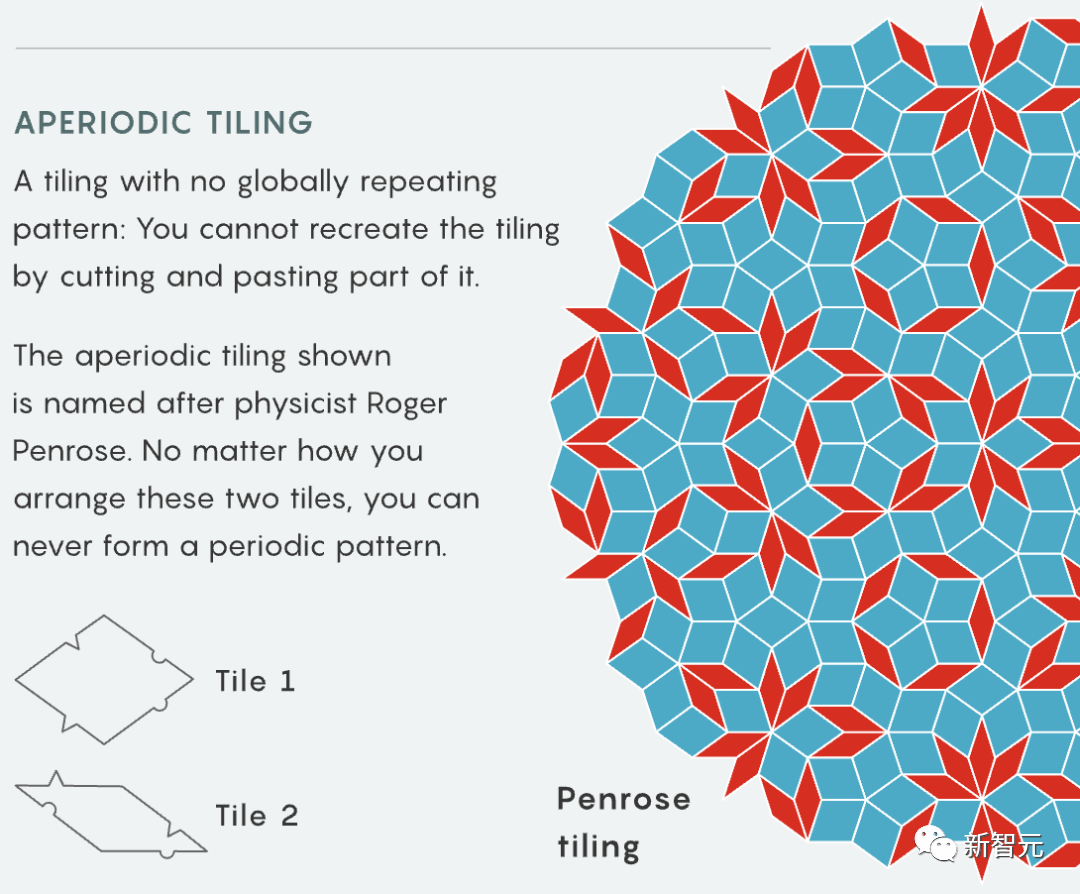
Tao Zhexuan a dit qu'il est un peu étrange que la plupart des composants présentés dans l'article soient similaires aux jeux populaires -

Les tuiles analogues des dominos, le Sudoku, le jeu informatique "Tetris" " , même le jeu pour enfants "Fizz buzz" est apparu

Pourquoi l'étude d'un problème de mathématiques implique-t-elle autant de jeux ? Tao Zhexuan ne peut pas non plus expliquer l'indécidabilité du pavage dense simple translationnel. Cet article est une suite de l'article précédent des deux. Problème de tuile périodique de lien

Dans le dernier article, ils ont construit un pavage dense unique translationnel d'une grille de haute dimension

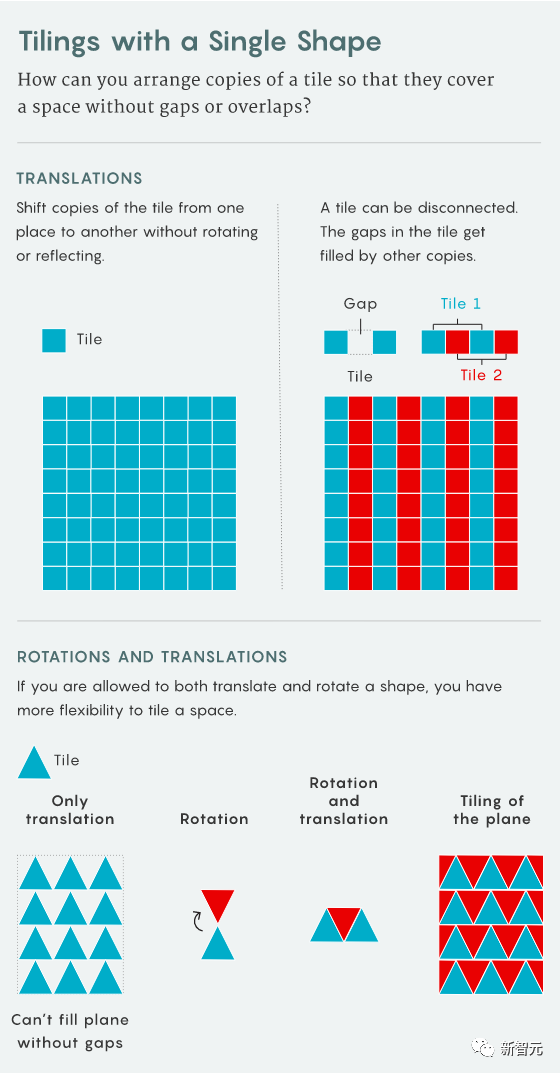
(donc un pavage dense unique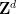 est un ensemble fini), il est non périodique (il n'y a aucun moyen de "fixer" ce pavage en un pavage périodique 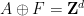, où

est désormais périodique par rapport au sous-groupe d'indice fini

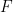
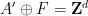
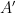). Ce fait nie l'hypothèse de Stein, Grunbaum-Shephard et Lagarias-Wang sur la non-existence de monomères apériodiques densément emballés 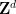("Hat single densément emballé" est un monomère isométrique apériodique récemment découvert carrelage dense

, dans lequel la rotation, la réflexion et la translation sont autorisées, ou le nouveau "monolithe fantôme" est similaire au carrelage dense unique, sauf qu'il n'est pas requis).

L'une des raisons pour lesquelles Tao Zhexuan et Rachel Greenfeld ont inspiré cette conjecture est l'observation du mathématicien Hao Wang

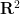Il a découvert que si la conjecture du carrelage périodique est vraie, alors le problème du carrelage translationnel est déterminable par un algorithme ——

Il existe une machine de Turing, pour 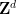, lorsqu'on lui donne une dimension 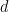et un sous-ensemble fini 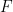, elle peut être déterminée dans un temps limité si 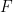peut être pavé .

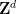En effet, s'il y a un carrelage périodique, il peut être trouvé grâce à une recherche informatique

S'il n'y a pas de carrelage du tout, alors on peut savoir grâce au théorème de compacité qu'il existe des finis 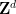sous-ensembles, ces sous-ensembles ne peuvent pas être couverts par des traductions 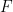disjointes, qui peuvent également être découvertes par recherche informatique.

La conjecture de pavage périodique affirme que ce sont les deux seules situations possibles, donnant ainsi la décidabilité.

D’un autre côté, le point de vue de Wang est immuable : l’échec de la conjecture de pavage périodique ne signifie pas automatiquement l’indécidabilité du problème de pavage unique translationnel, car il n’exclut pas l’existence d’autres algorithmes. déterminer le pavage, ce pavage peut être indépendant de l'existence d'un pavage périodique

(par exemple, même avec le pavage chapeau et fantôme récemment découvert, pour le simplexe isométrique de polygones à coefficients rationnels dans 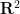Cela reste un domaine ouvert se demander si le problème du carrelage dense est décidable, avec ou sans réflexion

Les principaux résultats de cet article abordent cette question (avec une mise en garde) :

doit être revisité. Le contenu écrit est : Théorème 1

Il n'existe pas d'algorithme pour 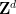, étant donné une dimension 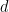, un sous-ensemble périodique 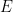et un sous-ensemble fini 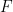, peut déterminer s'il existe un panoramique 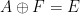à l'intérieur. une durée limitée

.

Il est important de noter qu'un sous-ensemble périodiqu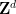e de 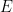doit être utilisé, plutôt que la totalité de 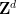; cela est en grande partie dû aux limites techniques de cette approche et est susceptible d'être obtenu par des efforts supplémentaires et créativité à éliminer.

De plus, Terence Tao et Rachel Greenfeld ont également remarqué que lorsque 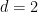, la conjecture périodique de la chaussée a été établie par Bhattacharya, donc le problème est décidable dans ce cas .

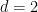Pour toute valeur fixe de 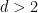, il reste à savoir si le problème de carrelage est décidable (notez que dans le résultat ci-dessus, la dimension 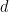n'est pas fixe, mais fait partie de l'entrée).

En raison du lien bien connu entre l'indécidabilité algorithmique et l'indécidabilité logique (également connue sous le nom d'indépendance logique), ce théorème implique également l'existence d'une dimension (en principe descriptible sans ambiguïté) 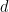Les sous-ensembles périodiques 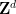de , 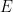et le sous-ensemble fini 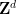de 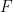font que 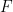réussit le carrelage de traduction 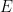et ne peut pas être confirmé ou falsifié dans la théorie des ensembles ZFC (bien sûr en supposant que la théorie soit cohérente).

Grâce à cette approche, nous pouvons également remplacer ici par le groupe "presque bidimensionnel" 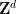, où 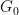est un groupe abélien fini (qui fait désormais partie de l'entrée, à la place des Dimensions ).

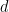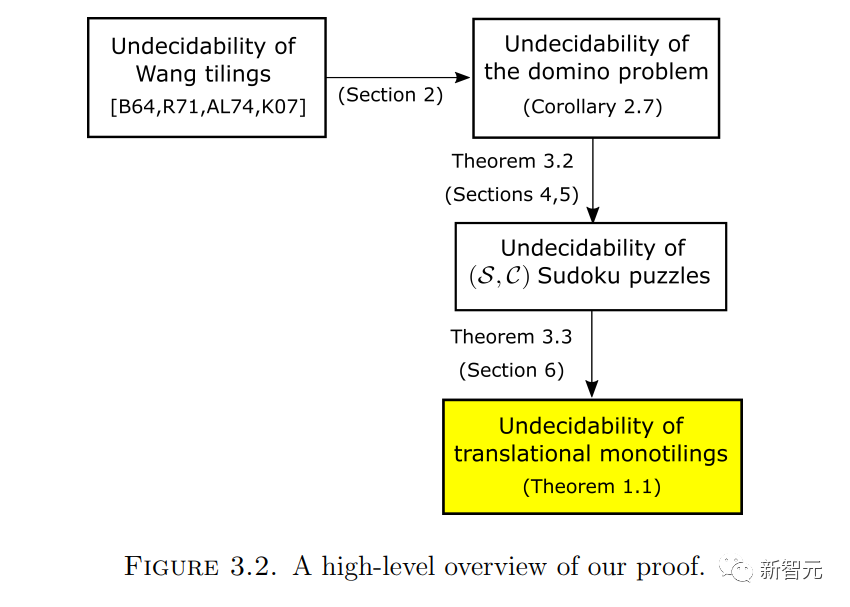
Ensuite, décrivez quelques-unes des idées principales de la preuve.

Une façon courante de prouver qu'un problème est indécidable consiste à "encoder" d'autres problèmes connus pour être indécidables dans le problème d'origine, de sorte que tout algorithme qui détermine le problème d'origine puisse également déterminer le problème intégré

Par conséquent, nous codons le problème de l'atelier dense de Wang comme un problème d'atelier dense unique  :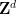

Le deuxième problème concerne le problème de l'atelier dense de Wang

Étant donné un Wang fini Pour un ensemble de tuiles 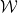(carrés unitaires, chaque bord se voit attribuer une certaine couleur à partir d'une palette limitée), est-il possible de tesseller le plan à l'aide d'une grille standard 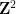par translation telle que les tuiles adjacentes aient la même couleur sur un terrain commun bord?

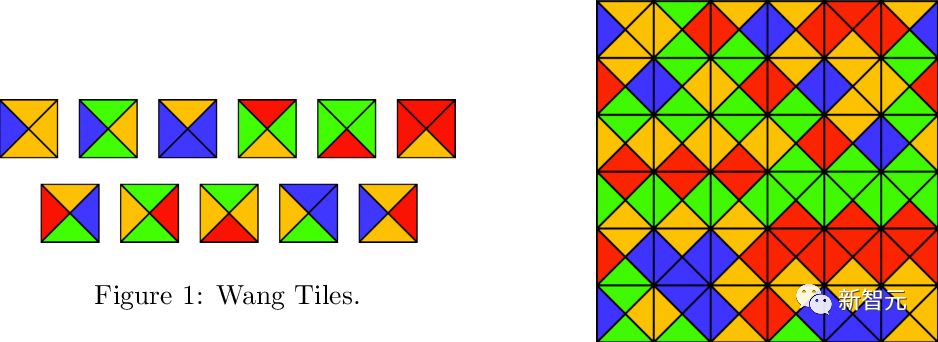
Berger a un jour tiré une conclusion célèbre selon laquelle ce problème ne peut pas être déterminé

Ce qui doit être réécrit est : Berger, Robert,

Convertir ce problème en un problème de haut niveau Le problème de carrelage dense unique par traduction dimensionnelle doit résoudre certains problèmes intermédiaires

Tout d'abord, nous pouvons facilement intégrer le problème de carrelage dense de Wang dans un problème similaire, que nous appelons le problème des dominos :

Réécrit comme suit : Le problème des dominos est le problème 3

Étant donné un ensemble fini de dominos horizontaux (ou verticaux) 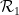ou 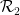, qui sont une paire de cellules adjacentes Carré, chaque carré unitaire est décoré avec un élément point dans l'ensemble fini 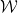. Est-il possible d'attribuer un point à chaque carré unitaire dans le carrelage en treillis standard 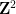, de sorte que chaque paire de ce carrelage puisse utiliser des carrés horizontaux (ou verticaux) avec des dominos de . 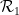ou ?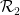

En fait, il suffit d'insérer chaque tuile de Wang comme un "point" séparé et de définir l'ensemble de dominos 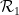, 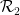pour qu'il soit adjacent horizontalement ou verticalement, avec des bords ayant des paires de secrets de Wang de la même couleur.

Dans les prochaines étapes, nous combinerons le problème des dominos avec le problème du Sudoku :

Problème 4 (Problème Sudoku)

Étant donné la largeur de la colonne 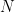, l'ensemble des nombres 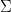, l'ensemble des fonctions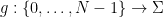 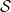et les "conditions initiales" 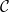（ Sans entrer dans les détails ici), est-il possible d'attribuer un numéro 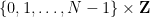à chaque cellule 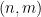du "Tableau Sudoku" 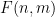, de sorte que pour n'importe quelle pente 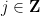et intercepter 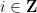, Le nombre 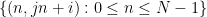le long de la ligne 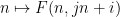se situe dans 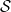(et 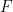obéit à la condition initiale ) ?

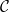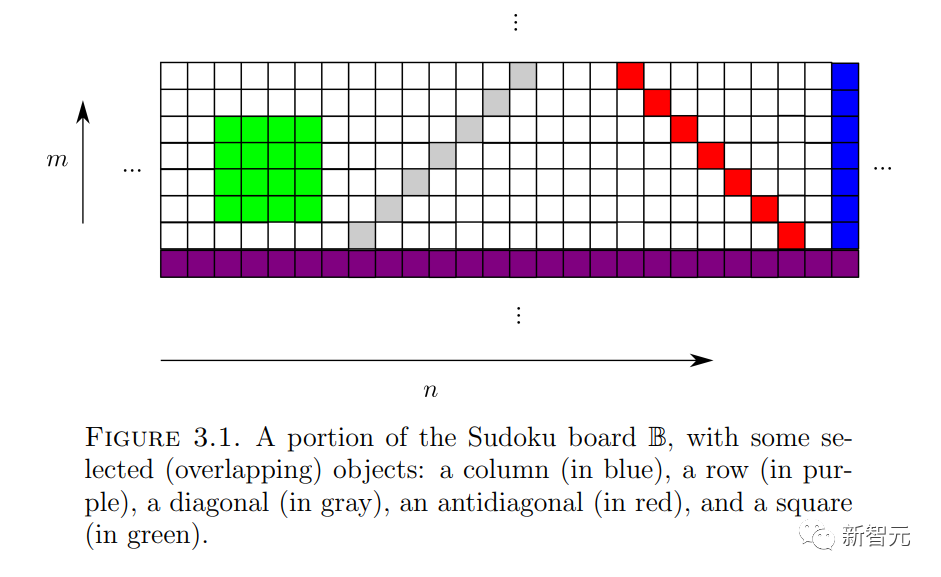
La partie la plus originale de cet article est de prouver que le problème des dominos peut effectivement être intégré dans un problème de Sudoku.

L'intégration du problème du Sudoku dans un problème de chiffrement unique est basée sur la méthode modifiée proposée dans les articles précédents

Ces articles ont également proposé différentes versions du problème du Sudoku et ont créé une méthode appelée "chiffrement". La méthode du "Padding" Langage" peut convertir divers problèmes (y compris les problèmes de Sudoku) en un seul problème de pavage

Pour encoder le problème de domino en problème de Sudoku, nous devons obtenir une fonction domino

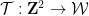(obéir aux contraintes de domino associées à certains jeu de dominos 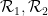) et l'utiliser pour construire une fonction Sudoku 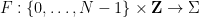(obéir à certaines contraintes Sudoku associées au jeu de dominos à l'inverse, chacun obéit au nombre Les fonctions Sudoku des règles du puzzle Sudoku doivent être générées à partir de la fonction domino) ; en quelque sorte.

Cette approche n'est pas immédiatement évidente, mais Tao et Rachel Greenfeld ont adapté certaines idées d'Aanderaa et Lewis avec l'aide d'Emmanuel Jeandel, et certaines hiérarchies ont été utilisées pour encoder un problème dans un autre.

Nous expliquons ici la structure hiérarchique 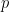(en raison de la nature bidimensionnelle du problème des dominos, deux nombres premiers différents doivent être utilisés).

Ensuite, construisez la fonction Sudoku 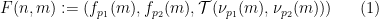avec 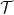via la formule 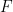, qui incarnera une sorte d'intégration.

où 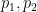sont deux grands nombres premiers différents (par exemple, vous pouvez prendre 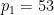, 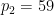), 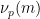représente le nombre de fois 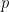est divisé par 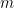, et

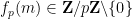est le dernier nombre non nul dans l'expansion de  :

(

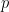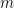
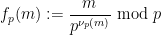, et 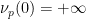). Dans le cas de 情况, la première composante de (1) est présentée ci-dessous :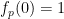

L'exemple typique du poids final 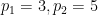est présenté ci-dessous :

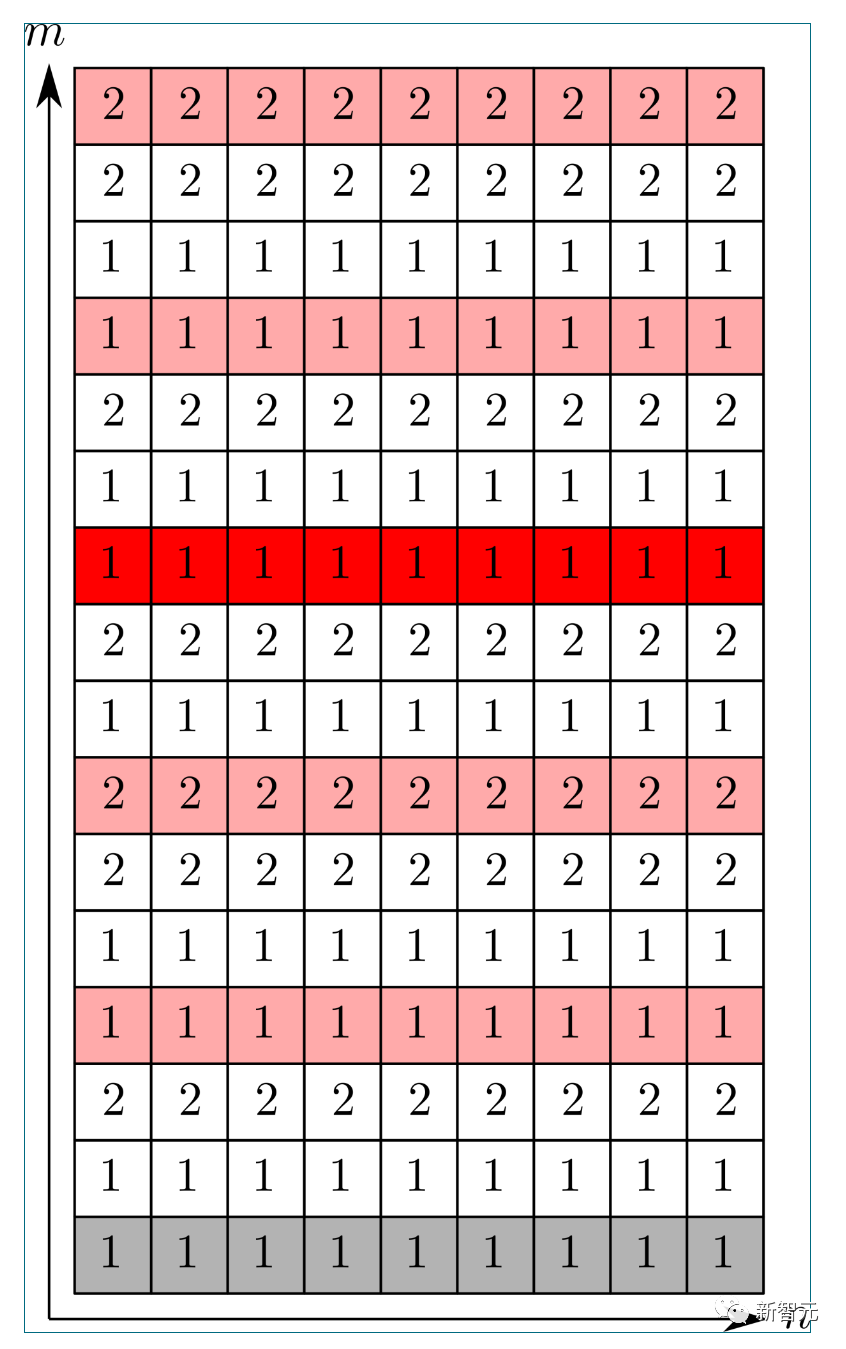
Fait intéressant, pour une raison quelconque , la décoration ici suit essentiellement les règles du jeu pour enfants "Fizz buzz"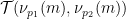

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!