Pensée inversée : le nouveau modèle de langage de raisonnement mathématique MetaMath entraîne de grands modèles

Le raisonnement mathématique complexe est un indicateur important pour évaluer les capacités de raisonnement des grands modèles de langage. Actuellement, les ensembles de données de raisonnement mathématique couramment utilisés ont des tailles d'échantillon limitées et une diversité de problèmes insuffisante, ce qui entraîne le phénomène de « renversement de la malédiction » en général. modèles de langage, c'est-à-dire un modèle formé sur « A ». Le modèle de langage de « est B » ne peut pas être généralisé à « B est A » [1]. La forme spécifique de ce phénomène dans les tâches de raisonnement mathématique est la suivante : étant donné un problème mathématique, le modèle de langage est efficace pour utiliser le raisonnement direct pour résoudre le problème, mais n'a pas la capacité de résoudre le problème avec un raisonnement inverse. Le raisonnement inversé est très courant dans les problèmes mathématiques, comme le montrent les 2 exemples suivants.

1. Question classique - Poulet et lapin dans la même cage

• Raisonnement avancé : Il y a 23 poules et 12 lapins dans la cage. Combien de têtes et combien de pieds y a-t-il dans la cage ?
• Raisonnement inverse : Il y a plusieurs poules et lapins dans la même cage. En comptant du haut, il y a 35 têtes, et en comptant du bas, il y a 94 pattes. Combien y a-t-il de poules et de lapins dans la cage ?

2. Problème GSM8K

• Raisonnement direct : James achète 5 paquets de bœuf de 4 livres chacun. Le prix du bœuf est de 5,50 $ la livre ?
• Raisonnement inversé. : James achète x paquets de bœuf de 4 livres chacun. Le prix du bœuf est de 5,50 $ par livre. Si nous savons que la réponse à la question ci-dessus est 110, quelle est la valeur de la variable inconnue x ?

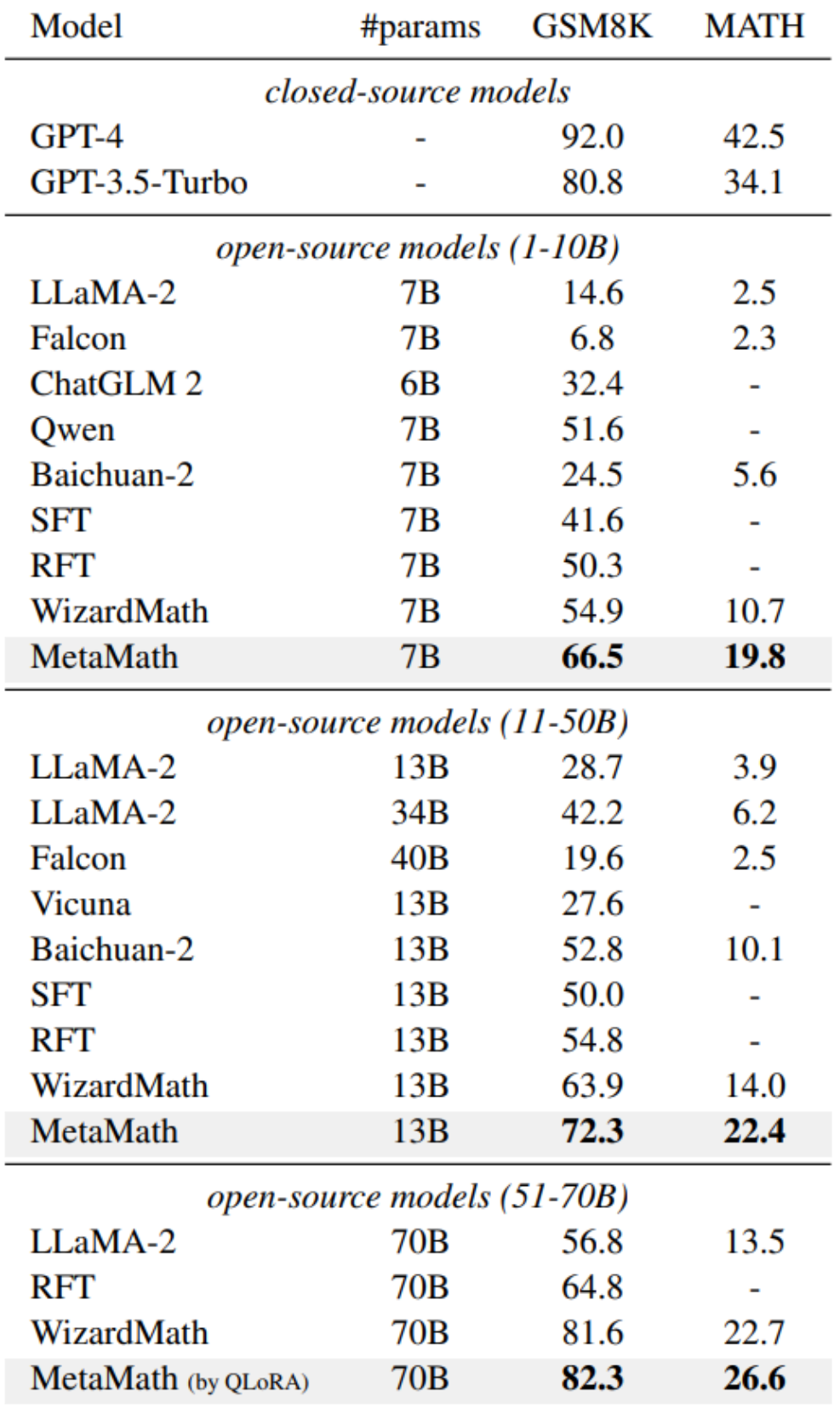
Afin d'améliorer les capacités de raisonnement avant et arrière du modèle, des chercheurs de Cambridge, de l'Université des sciences et technologies de Hong Kong et de Huawei ont proposé l'ensemble de données MetaMathQA basé sur deux ensembles de données mathématiques couramment utilisés (GSM8K et MATH) : un avec une large couverture et un ensemble de données de raisonnement mathématique de haute qualité. MetaMathQA se compose de 395 000 paires de questions-réponses mathématiques avant-inverse générées par un grand modèle de langage. Ils ont affiné LLaMA-2 sur l'ensemble de données MetaMathQA pour obtenir MetaMath, un grand modèle de langage axé sur le raisonnement mathématique (vers l'avant et l'inverse), qui a atteint SOTA sur l'ensemble de données de raisonnement mathématique. L'ensemble de données MetaMathQA et les modèles MetaMath à différentes échelles ont été open source pour être utilisés par les chercheurs.

• Adresse du projet : https://meta-math.github.io/
• Adresse papier : https://arxiv.org/abs/2309.12284
• Adresse des données : https : //huggingface.co/datasets/meta-math/MetaMathQA
• Adresse du modèle : https://huggingface.co/meta-math
• Adresse du code : https://github.com/meta-math/ MetaMath

Dans l'ensemble de données GSM8K-Backward, nous avons construit une expérience d'inférence inverse. Les résultats expérimentaux montrent que par rapport aux méthodes telles que SFT, RFT et WizardMath, la méthode actuelle est peu performante sur les problèmes d'inférence inverse. En revanche, le modèle MetaMath atteint d'excellentes performances en inférence directe et inverse. 1. Augmentation des réponses :

Face à une question, une chaîne de réflexion capable d'obtenir le résultat correct est générée via un grand modèle de langage en tant qu'augmentation des données.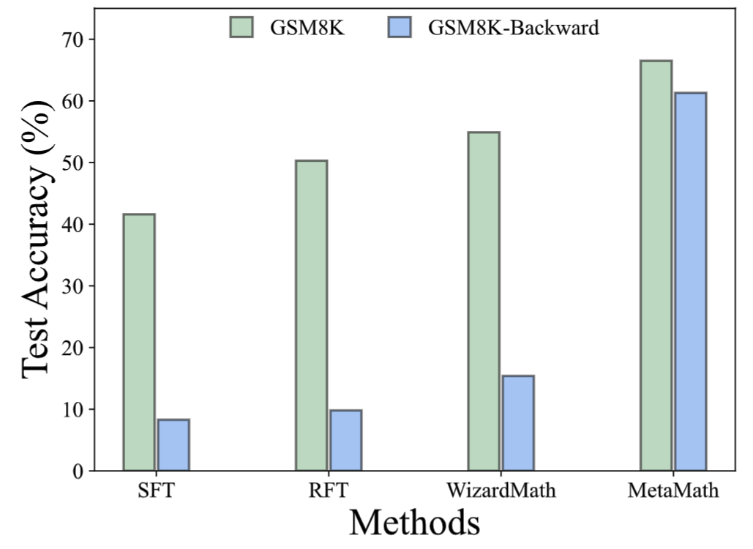

Question : James achète 5 paquets de bœuf de 4 livres chacun Le prix du bœuf est de 5,50 $ la livre ?

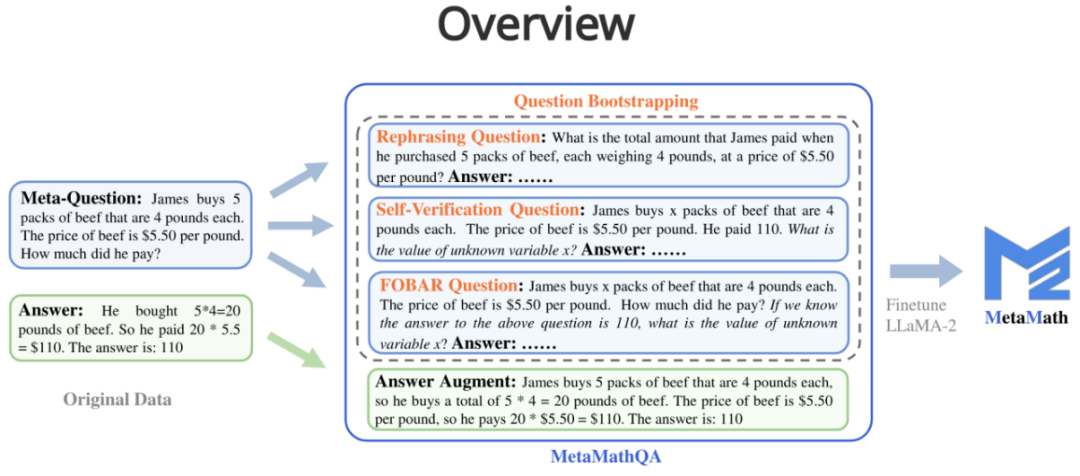Réponse : James achète 5 paquets de bœuf de 4 livres. chacun, donc il achète un total de 5 * 4 = 20 livres de bœuf. Le prix du bœuf est de 5,50 $ la livre, donc il paie 20 * 5,50 $ = 110 $. La réponse est : 110.

2. Question (amélioration de la réécriture des questions) :

À partir d'une méta-question, réécrivez la question à travers un grand modèle de langage et générez une chaîne de réflexion qui obtient le résultat correct en tant qu'augmentation des données.

• Question : Quel est le montant total que James a payé lorsqu'il a acheté 5 paquets de bœuf, pesant chacun 4 livres, au prix de 5,50 $ la livre ?
• Réponse : Chaque paquet de bœuf pèse 4 livres, donc 5 les paquets pèsent 4 * 5 = 20 livres au total. Le prix par livre de bœuf est de 5,50 $, donc le coût total pour 20 livres est de 20 * 5,50 $ = 110 $. Par conséquent, James a payé un total de 110 $. La réponse est : 110..

3. Question FOBAR (amélioration de la question inverse FOBAR) : Étant donné une méta-question, le nombre dans la condition de masque est x, étant donné la réponse originale et l'inverse de x pour générer une question inverse, et basé sur Ce problème inverse génère la chaîne de pensée correcte pour effectuer une augmentation des données (exemple d'inversion : « Si nous savons que la réponse à la question ci-dessus est 110, quelle est la valeur de la variable inconnue x ? »).

• Question : James achète x paquets de bœuf de 4 livres chacun. Le prix du bœuf est de 5,50 $ la livre. Si nous savons que la réponse à la question ci-dessus est de 110, quelle est la valeur ? de variable inconnue x ?
• Réponse : James achète x paquets de bœuf de 4 livres chacun, il achète donc un total de 4x livres de bœuf. Le prix du bœuf est de 5,50 $ la livre, donc le coût total du bœuf. est 5,50 * 4x = 22x. On nous donne que le coût total est de 110 $, nous pouvons donc écrire : 22x = 110. En divisant les deux côtés par 22, nous obtenons : x = 5. La valeur de x est 5.

4. Question d'auto-vérification (amélioration de la question inverse d'auto-vérification) : Basée sur FOBAR, l'augmentation des données est effectuée en réécrivant la partie de la question inverse en déclarations énoncées via un grand modèle de langage (exemple réécrit : "Combien a fait il paie ? » (avec la réponse 110) a été réécrit comme « Il a payé 110 »).

• Question : James achète x paquets de bœuf de 4 livres chacun. Le prix du bœuf est de 5,50 $ la livre. Il en a payé 110. Quelle est la valeur de la variable inconnue x ?
• Réponse : Pour résoudre ce problème. problème, nous devons déterminer la valeur de x, qui représente le nombre de paquets de bœuf que James a achetés. Chaque paquet de bœuf pèse 4 livres et coûte 5,50 $ par livre. Le montant total que James a payé est de 110 $. comme suit : Nombre de paquets de bœuf * Poids par paquet * Prix par livre = Montant total payé ; x * 4 * 5,50 $ = 110 $ ; nous divisons les deux côtés de l'équation par 22 : 22x / 22 = 110 $ / 22 ; x = 5 $ ; La valeur de x est 5. Les résultats expérimentaux sur des ensembles de données de raisonnement mathématique (GSM8K et MATH) montrent que MetaMath est nettement meilleur que l'existant. modèle LLM open source en termes de performances et ne nécessite pas l'utilisation d'outils externes (tels que des interpréteurs de code). Parmi eux, notre modèle MetaMath-7B atteint une précision de 66,5 % sur GSM8K et de 19,8 % sur MATH, soit respectivement 11,6 % et 9,1 % de plus que les modèles de pointe de la même échelle. Il convient particulièrement de mentionner que MetaMath-70B a atteint une précision de 82,3 % sur GSM8K, dépassant GPT-3.5-Turbo

Selon « l'hypothèse d'alignement de surface » [2], la capacité des grands modèles de langage vient de pré- formation, tandis que les données des tâches en aval activent les capacités inhérentes du modèle de langage appris lors de la pré-formation. Par conséquent, cela soulève deux questions importantes : (i) quel type de données active le plus efficacement les connaissances latentes, et (ii) pourquoi un ensemble de données est-il meilleur qu’un autre pour une telle activation ?

Pourquoi MetaMathQA est-il utile ? Amélioration de la qualité (perplexité) des données de la chaîne de réflexion

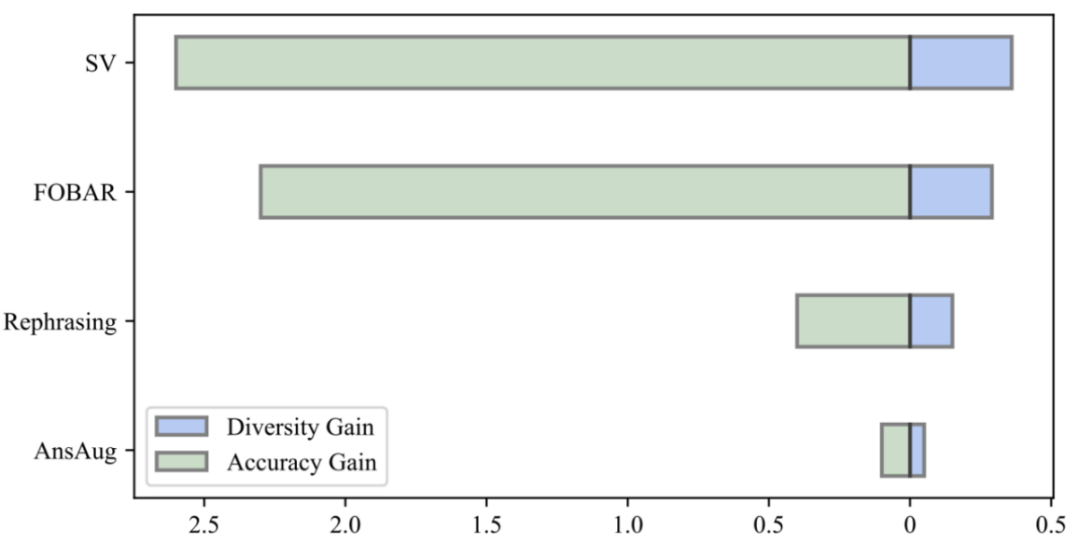
Comme le montre la figure ci-dessus, les chercheurs ont calculé le modèle LLaMA-2-7B dans chaque partie des données de réponse uniquement, GSM8K CoT et les données MetaMathQA définissent le niveau de confusion. La perplexité de l'ensemble de données MetaMathQA est nettement inférieure à celle des deux autres ensembles de données, ce qui indique qu'il a une plus grande capacité d'apprentissage et peut être plus utile pour révéler la connaissance latente du modèle

Pourquoi MetaMathQA est-il utile ? Augmentation de la diversité des données de la chaîne de pensée

En comparant le gain de diversité des données et le gain de précision du modèle, les chercheurs ont constaté que l'introduction de la même quantité de données augmentées par reformulation, FOBAR et SV entraînait des gains de diversité évidents et une amélioration significative du modèle. précision. En revanche, l’utilisation seule de l’augmentation des réponses a entraîné une saturation significative de la précision. Une fois que la précision atteint la saturation, l'ajout de données AnsAug n'apportera qu'une amélioration limitée des performances

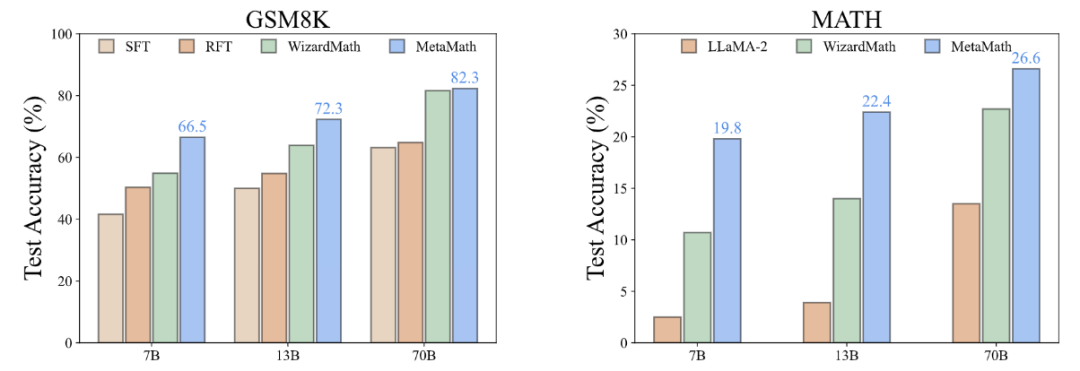
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!